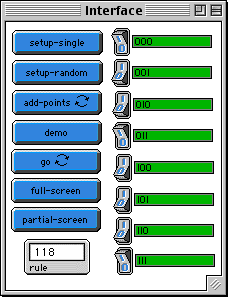
WHAT IS IT? ----------- This program models one-dimensional cellular automata. A cellular automaton is a computational machine that performs actions based on certain rules. It can be thought of as a "board" which is divided into cells (such as the square cells of a checkerboard). Each cell can be either on or off. This is called the "state" of the cell. According to specified rules, each cell will be on (alive) or off (dead) at the next time step. In this case of one-dimensional cellular automata, each cell checks the state of itself and its neighbors to the left and right, and then sets the cell below itself to either on or off, depending upon the rule. This is done in parallel and continues until the bottom of the board. Cellular automata can be created on any board size and dimension. HOW TO USE IT ------------- There are two settings, PARTIAL-SCREEN and FULL-SCREEN. The difference is that the FULL-SCREEN gives a larger board to view, while the PARTIAL-SCREEN will allow a demo mode. Click DEMO (while in PARTIAL-SCREEN mode) to see what the current rules will produce for each of the possible states of a cell's neighborhood. The rules are set by the eight switches on the right. The names of the switches correspond to cell states. "O" means off, "I" means on. For example, the top switch is called "OOO". (NOTE: the switch names are composed of the letters "I" and "O", not the numbers zero or one). If this switch is set to 1, then the following rule is created: when a cell is off, its left neighbor cell is off and its right neighbor cell is off, then the cell below it will be set on at the next time step. If this switch is set to 0, then the cell below it will be set to off at the next time step. So, since each switch has two settings and there are eight switches, there are 256 (2^8) possible rules. The current rule number is shown in the "RULE" monitor, and it is calculated by changing a switch's name from binary to decimal and taking the sum of all the switches that are set to one. For example, if "011" and "001" are set to 1 and all the rest are set to 0, then the rule number is 4 (011=3, 001=1, 3+1=4)). To make the time step, click GO. There are three ways to setup the initial line of cells. SETUP-SINGLE will start with a single cell set to on in the center of the board. SETUP-RANDOM will start with a line of cells that have a random amount set to on. This density can be controlled with the global variable 'density. The third way is to add points by clicking the mouse. Click on ADD-POINTS and then click the mouse along the first row to set various cells to on. The background color and foreground color can be set via the global variables 'fgcolor' and 'bgcolor'. RUNNING the MODEL ----------------- THINGS TO NOTICE ---------------- What different patterns are formed by using a random setup and a single setup? Why do some rules always end up the same, regardless of how it is initially started? Are there rules that repeat a pattern indefinitely? Are there rules that produce seemingly chaotic, random results? Can all rules be classified into these above types? Are there more rule types than these? THINGS TO TRY ------------- Find some rules that converge to all cells on or all cells off. Are there any rules that converge to all cells on or all cells off, depending upon the initial percentage of on/off cells? A classic automaton is used to compute various things. Can these cellular automata be used to compute anything? How? Experiment with the density variable and various types of rules. What are some relationships? EXTENDING THE MODEL ------------------- What if a cell's neighborhood was five - two to the left, itself, and two to the right? Try making a two-dimensional cellular automaton. The neighborhood could be the eight cells around it, or just the cardinal cells (the cells to the right, left, above, and below). STARLOGOT FEATURES ----------------- Notice the use of "mouse-xcor" and "mouse-ycor" to allow the user to interact withe the simulation in the graphics window. Examine the use of the "setvariable-at x y" command to allow the patches to get information about their neighbors.