WHAT IS IT?
-----------

This is a new kind of mathematical investigation. Turtles
are circling on a circle of a fixed radius. What happens if
the radius they are all circling at is changed?

HOW TO USE IT
-------------

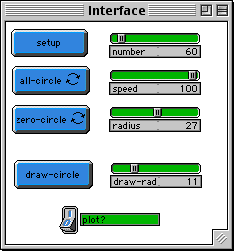
The NUMBER slider determines the number of turtles circling.
The RADIUS slider determines the size of the circle each
turtle moves on.
The SPEED slider determines how large a step each turtle take
at each clock tick -- it determines the speed of circling.

The SETUP button creates NUMBER turtles on a circle of
radius RADIUS centered at the point (0 0). The turtles are all
headed so as to move around the circle.

The ALL-CIRCLE button starts the turtles circling. They are
each drawing their own circle of radius RADIUS.

Change the value of the RADIUS slider while the turtles
are circling.  Before you do it, what is your guess as to
what will happen when you change the RADIUS?

RUNNING the MODEL
-----------------

        THINGS TO NOTICE
        ----------------

What is happening to the shape described by the turtles?
How far out do the turtles go?
How far in do they come?


        THINGS TO TRY
        -------------

Try different values of both starting radius and
changed radius. 

You can also do further investigations with the following controls:
 
The ZERO-CIRCLE button lets you just focus on turtle zero's movement --
all the rest are stopped.

The DRAW-CIRCLE button lets you draw a circle on the patches with a
radius equal to DRAW-RAD. This way you can show the range of the
oscillating circles.

If the PLOT? switch is on, Plotwindow1 will show a plot of turtle
zero's distance from the origin as the turtles circle.  

Try the command  LT 50  while the turtles are circling. Is
this the same behavior as you observed when changing the radius?

In the Command Center, get a single (or several) turtles to trace their
path using the command pendown (pd).  This may help to show the
relationship between the circles of individual turtles and the circle
you see as they all move together.  

EXTENDING THE MODEL
-------------------

What tools can you build to help visualize what is going on?

STARLOGOT FEATURES
-----------------

Notice the behavior of the StarLogoT function ATAN. It gives
positive values for x positive, so it is necessary to
multiply x by -1 in order to get the tangent angles for the circle.