GASLAB: FREE GAS
WHAT IS IT?
-----------
This program simulates the behavior of gas molecules.
It was one of the original CM StarLogo applications (under the name
GPCEE) and is now ported to StarlogoT as part of the Connected
Mathematics "Making Sense of Complex Phenomena" Modeling Project.
The Free-Gas model is one in a collection of GasLab
models that use the same basic rules for expressing what happens
when gas molecules collide. Each one has different features in
order to show different aspects of the behavior of gases. This
model is the simplest, and the basic interaction of molecules
here is used in all the other models.
Molecules are modeled as perfectly elastic particles with
no internal energy except that which is due to their motion.
Collisions between molecules are elastic. The molecules wrap
thescreen, that is, if they leave one edge they reappear on the
other edge. Particles are colored according to speed -- blue
forslow, green for medium, and red for high speeds.
The exact way two molecules collide is as follows:
1. Two turtles "collide" if they find themselves on the same
patch.
2. A random axis is chosen, as if they are two balls that hit
each other and this axis is the line connecting their centers.
3. They exchange momentum and energy along that axis, according
to the conservation of momentum and energy. This calculation is
done in the center of mass system.
4. Each turtle is assigned its new velocity, energy, and heading.
5. If a turtle finds itself on or very close to a wall of the
container, it "bounces" -- that is, reflects its direction and
keeps its same speed.
HOW TO USE IT
-------------
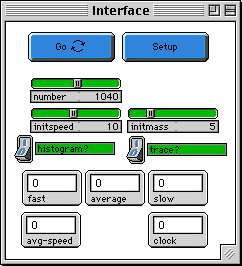
SETUP: puts in the initial conditions you have set with the
sliders. Be sure to wait till the Setup button stops before
pushing go.
GO: runs the code again and again. This is a "forever" button.
NUMBER:the number of gas molecules
INITSPEED: the initial speed of each molecule -- they all
start with the same speed.
INITMASS: the mass of each molecule.
PLOT?: If this equals 1, the histograms are plotted every 6
ticks. The plotting frequency can be modified with the variable
"plotfrq".
TRACE?: Stamps the path of one individual molecule. This path
fades in time to make the screen less cluttered.
FAST, AVERAGE, SLOW MONITORS: numbers of molecules with different
speeds: fast (red), average (green), and slow (blue).
AVG-SPEED: average speed of the molecules.
CLOCK: number of ticks that have run.
GRAPHS:
ENERGY HISTOGRAM (1): the distribution of energies of all the
molecules, calculated as m*v*v/2. The yellow line is the
average value.
SPEED HISTOGRAM (2): speed distribution of all the molecules.
Theyellow line is the initial average value. The running average
value is shown in a monitor. The red and blue lines mark the
limits of "fast" and "slow" molecules.
SPEED COUNTS (3): plots the number of molecules in each range of
speed.
Initially, all the molecules have the same speed
but random directions. Therefore the first histogram plots of
speed and energy should show sharp spikes. As the molecules
repeatedly collide, they exchange energy and head off in new
directions, and the speeds are dispersed -- some molecules
get faster, some get slower.
RUNNING the MODEL
-----------------
THINGS TO NOTICE
----------------
What is happening to the numbers of molecules of different
colors? Does this match what's happening in the histograms?
Why are there more blue molecules than red ones?
Can you observe collisions and color changes as they happen?
For instance, When a red molecule hits a green molecule, what color
do they each become?
Why does the average speed (avg-speed) drop? Does this violate
conservation of energy?
The molecule histograms quickly converge on the classic Maxwell-
Boltzman distrbution. What's special about these curves? Why is
the shape of the energy curve not the same as the speed curve?
This gas is in "endless space" -- no boundaries, no obstructions,
but still a finite size! Is there a physical situation like
this?
Watch the molecule whose path is traced in yellow. Notice how the
path "wraps" the screen. Does the trace resemble Brownian motion?
Can you recognize when a collision happens? What factors affect
the frequency of collisions? What about the "angularity" of the
path? Could you get it to stay "local" or travel all over the
screen?
In what ways is this model an incorrect idealization of the real world?
THINGS TO TRY
-------------
Set all the molecules in part of the screen,or with the same
heading -- what happens? Does this correspond to a physical
possibility?
Try different settings, especially the extremes. Are the
histograms different? Does the trace pattern change?
Are there other interesting quantities to keep track of?
Look up or calculate the REAL number, size, mass and speed of
molecules in a typical gas. When you compare those numbers to
the ones in the model, are you surprised this model works as well
as it does? What physical phenomena might be observed if there
really were a small number of big molecules in the space around
us?
We often say outer space is a vacuum. Is that really true? How
many molecules would there be in a space the size of this
computer?
EXTENDING THE MODEL
-------------------
Could you find a way to measure or express the "temperature"of
this imaginary gas? Try to construct a thermometer.
What happens if there are molecules of different masses? (See
Two Gas model.)
How would you define and calculate pressure in this "boundless"
space?
What happens if the collisions are non-elastic?
How does this 2-D model differ from the 3-D model?
Set up only two molecules to collide head-on. This may help to
show how the collision rule works. Remember that the axis of
collision is being randomly chosen each time.
What if some of the molecules had a "drift" tendency -- a force
pulling them in one direction? Could you develop a model of a
centrifuge, or charged particles in an electric field?
Find a way to monitor how often molecules collide, and how far
they go between collisions, on the average. The latter is called
the "mean free path". What factors affect its value?
In what ways is this idealization different from the idealization
that is used to derive the Maxwell-Bolzmann distribution?
Specifically, what other code could be used to represent the
two-body collisions of molecules?
If MORE than two molecules arrive on the same patch, the current
code says they don't collide. Is this a mistake? How does it
affect the results?
Is this model valid for fluids in any aspect? How could it be
made to be fluid-like?
STARLOGO FEATURES
-----------------
During each tick, each turtle checks many times to see if it has
collided.
Notice the use of the plot window to do histograms. Histograms
can also be implemented using the StarLogo window.
Notice how collisions are detected by the turtles and how the
code guarantees that the same two particles do not collide twice.
What happens if we let the patches detect them?
You can find specific values on the graphs by clicking the mouse
on the point whose value you would like. The coordinates of that
point are shown in red.
