Random Walk (360)
WHAT IS IT?
-----------
In this model the turtles engage in a "random walk."
Each turtle walks one step away from its current location
at each clock tick.
The turtles walk along a random integer angle, theta, that
is between 0 and 360 degrees.
This movement is known as walking a 360-gon "lattice."
A lattice is a set of points on the plane (or in space) that
form a grid on which turtles walk.
As the simulation continues, one can expect the turtles to
become more spread out. Will they ever return home?
Observe the kinds of patterns that develop as the turtles
move.
HOW TO USE IT
-------------
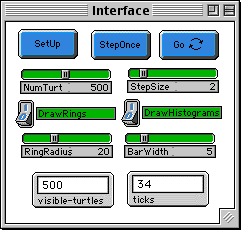
General Settings
----------------
Use the NUMTURT slider to select how many turtles will
participate in the random walk.
Use the STEPSIZE slider to decide how far from its current
location a turtle will move on each step.
How steps are implemented:
If STEPSIZE is set to 1 it will add cos(theta) to its
current xcor value and it will add sin(theta) to its
current ycor value. It will have moved one patch unit
from its current location.
(Why?)
If STEPSIZE is set to n it will add (n * cos(theta)) to its
current xcor value and it will add (n * sin(theta)) to its
current ycor value. It will have moved n patch units
from its current location.
(Why?)
Each of the above movements would be considered a single
"pace."
Distance Rings
--------------
Set DRAWRINGS to 1 to draw the x-axis, y-axis, and a
set of concentric circles about the point (0 0). This switch
must be set prior to pressing SETUP.
Use the RINGRADIUS slider to set the incremental distance
between the distance rings. The distance is measured along a
radius of
the circles.
The Six Plot Windows
---------------------
'Random Walk (360)' takes advantage of StarLogoT's multiple
plot windows. There are six different graphs available at any
one time:
"Average Distance Over Time (1)"
-measures the average distance over all turtles, from
home (the origin at 0,0) to their current coordinates.
"Average X-Distance Over Time (2)"
-measures the average distance over all turtles along the
x-axis away from the origin (x = 0).
"Standard Deviation Over Time (3)"
-measures the standard deviation of all turtles' true
distance from home to their current position. Sample
standard deviation is used.
"Average Distance Histogram (4)"
-measures turtles' true distance from home, using their
current coordinates. It displays a histogram showing how
many turtles are at a given distance from home.
"X-Distance Histogram (5)"
-measures distance based on turtles' xcor values. It
displays a histogram showing how many turtles are at a
given distance from the y-axis (where x = 0).
"Y-Distance Histogram (6)"
-measures distance based on turtles' ycor values. It
displays a histogram showing how many turtles are at a
given distance from the x-axis (where y = 0).
Note that xcor and ycor values are stored in such a way that
turtles are tracked even if they move off the screen. These
'off screen' values are used to measure distances. They are
stored at turtle variable xc (for xcor) and yc (for ycor).
(WARNING: There is a bug in this version and off-screen
turtles are not tracked correctly)
Distances are either zero or positive.
Histogram Settings
------------------
Use the DRAWHISTOGRAMS switch to draw histograms, or turn off
histogramming to improve the speed of the model. This switch
can be used while the model is running.
Use BARWIDTH to set the width of the bars in the histogram.
Monitors
--------
The TICKS monitor displays how many paces the turtles have
taken.
The VISIBLE-TURTLES monitor displays how many turtles are
visible on the screen. Turtles that have moved off the
screen are 'hidden.'
Buttons
-------
Press SETUP when all of the above selections have been made.
This will create the selected number of turtles at the
bottom center of the screen.
Press STEPONCE to make the turtles move one pace.
Press GO to make the turtles move continuously.
To stop the turtles, press the GO button again.
RUNNING THE MODEL
-----------------
Try starting with 500 turtles with a step size of 2. Use a
a bar width of 5. If you want to
show distance rings, try setting the radius increment to 20.
Press SETUP then press GO.
The turtles all start at 0 0 (home).
Think about how you would define an 'average' turtle and an
'average' walk.
Where would you expect an average turtle to end up at a
given time? Why?
Will all turtles eventually return home? If so, how many
paces would you expect a turtle to travel before it returned
to home? Why?
What kinds of calculations or measurements would you use in
trying to answer these questions?
THINGS TO NOTICE
----------------
Two characteristics of the graphs you see are their
smoothness and their slope.
To think about smoothness of line graphs, notice much
the lines move up and down over time.
To think about slope of line graphs, consider whether the
graph appears to be going 'uphill' or 'downhill' and
consider whether the 'hill' is steep or flat.
To think about smoothness of histograms, consider how
jagged a pattern is formed by the upper parts of all the
bars in the histogram.
To think about the slope of histograms, consider how
quickly the height of bars change as you move away from
the center of the histogram.
What do you notice about the smoothness and slope of the
graphs?
- Are they smooth? Why or why not?
- Are they steep? Why or why not?
- For a given graph, is its steepness the same at the
far edges and at the center? Why or why not?
Does the graph have any symmetry? Would you expect
it to? Why?
Does a single line graph ever change between positive and
negative slopes? Why or why not? If it does, what does
that mean?
What kind of distribution pattern (if any) is shown in
the histograms?
THINGS TO TRY
-------------
Try to answer the following questions before running the
simulations. Record your predictions.
Compare your predicted results with the actual results.
- What reasoning led you to correct predictions?
- What assumptions that you made need to be revised?
Try different numbers of turtles while keeping all other
slider values the same.
- What happens to the graph's smoothness and slope when
the number of turtles is increased?
- What happens to the graph's smoothness and slope when
the number of turtles is decreased?
- Does the simulation finish faster or slower than the
first model?
Try different numbers of steps while keeping all other
slider values the same.
- What happens to the graph's smoothness and slope when
the number of steps is increased?
- What happens to the graph's smoothness and slope when
the number of turtles is decreased?
- Does the simulation finish faster or slower than the
first model?
Try different bar widths while keeping all other
slider values the same.
- What happens to the histogram's smoothness and slope when
the width of bars is increased?
- What happens to the histogram's smoothness and slope when
the width of bars is decreased?
One way to experiment with different bar widths for the
same simulation is as follows:
1. At the end of a simulation, display the plot window.
2. Change the value of BarWidth.
3. Enter the command "pw3 draw-histogram 0"
[without the quotes] in the command center.
(This tells StarLogoT to select the third plot window-
the one used for drawing the average distance
histogram- and then to draw that particular
histogram.)
4. Notice how the histogram changes.
How do your answers to the above questions compare to the
average values calculated for all turtles in a given
simulation?
EXTENDING THE MODEL
-------------------
In this simulation, turtles can only move based on integer
values of theta. Change the model so that any value of
theta between 0 and 360 degrees is possible.
Does this change the amount of time it would take for a
turtle to return home? How? Why?
How does this change impact answers to other questions
asked above?
StarLogoT now offers you six different plot windows in which
to draw graphs. One of these (the second) measures the
average x-distance away from the origin over all turtles.
Obviously,
it could have measured the y-distance instead. Watch the
graph under one run of the model, and then change the
procedure so that it measures y-distance. How do the graphs
differ?
Create a new monitor called home-turtles. Have it display
the number of turtles at (or very near) home. Create a plot
to display this information.
STARLOGOT FEATURES
-----------------
Text boxes are used help organize the sliders, switches,
monitors, and buttons.
Coloring of patches is used to draw a coordinate grid on the
turtle screen.
The plot windows are used to draw both line graphs and
histograms. Drawing histograms is a rather complex task- try
to work through the code for drawing them.
There are a total of six different plot windows. Each one
has its own set of six plot pens. You can switch between
plot windows exactly like you do for plot pens- the 'pw1'
primitive, for instance, selects the first plot window to be
the active graph; 'pw2' selects the second, etc... You can
also rename the windows with the 'setplotwindow-name'
command. See how the windows each have a different title,
that also shows up under the Plot Windows sub-menu. Finally,
each of these plot windows can be dynamically re-sized,
allowing you to view all of them on the screen at once.
