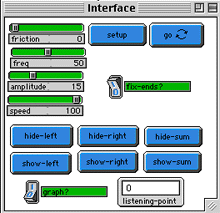
WHAT IS IT? ----------- This project simulates sound wave interference. There is one speaker at each end and each speaker is powered by a sinusoidal signal generator. The yellow line represents the sound level due to the left speaker, the cyan line represents the sound level due to the right speaker, and the red line represents the sum of the sound level due to both speakers. HOW TO USE IT ------------- Click the SETUP button to set up the system. Click GO to turn on the speakers. The FRICTION slider controls the amount of sound damping in the air. The FREQUENCY slider controls the frequency of the signal generator. The AMPLITUDE slider controls the sound level of the speakers. There are three buttons to hide each curve and three buttons to show each curve, so that the curves can be observed individually or collectively. Set the GRAPH toggle switch to 1 and click anywhere on the horizontal line in the Graphics Window and you will be able to observe the sound level vs. time at the position you selected. The LISTENING-POINT monitor shows the x coordinate of the point. It is also shown by a white vertical line in the Graphics Window. When the FIX-ENDS? toggle switch is on, the two sound waves are "anchored" at the ends opposite the speakers, as if the waves were ropes and the ends were tied down. THINGS TO NOTICE ---------------- Sound effect is due to pressure change spatially and temporally. The waveforms are made up of three lines of turtles. Each turtle acts as it were connected to its neighboring turtles with springs. When neighboring turtles are further away, they exert a stronger force. When the left end of the sound level goes up, it "pulls up" the turtle to its right, which in turn pulls up the turtle to its right, and so on. In that way, a sound wave moves through the air. The green turtles (speakers) continue to put more energy into the air. When there is no friction in the air, the waves in the air travel without losing amplitude. Try adding friction to see what it does to the waves. When two speakers are turned on, the sound level at a certain point at a certain time is the sum of the sound levels produced by the two speakers at that time. Its pattern may be quite different from either of the speaker sound patterns. THINGS TO TRY ------------ Change the values on the sliders and observe what happens to the sum of the sound level, the red curve. Try to create a "standing wave," in which some points on the lines do not move at all, and plot one of the point to see if the sum at this point is zero. Try to create a flat red curve. Compare a fixed-end system with an open-ended system. Some of the patterns are pretty wild! Compare the relationship between frequency and wavelength. Note that the "speed" here is the speed of the model, not the speed of the wave. Find a way to measure the speed of the wave such that the relationship, speed = frequency * wavelength, is true. EXTENDING THE MODEL ------------------- Program the red turtles to find the sum of the absolute values of the two waves. Make it possible to "fix" the waves to zero at some point along the line, not just the ends -- as if this were a string and you put your finger on it. Make the waves "reflect" from each end instead of going on. STARLOGO FEATURES ----------------- In order to have three independent waves, three lines of turtles are created -- yellow, then cyan, then red -- in order from left to right. Special turtles are created to control the ends of these waves. One end generates the wave (green) and the other end prevents the wave motion from wrapping (dark blue). For this project, it does not make sense for the turtles to "wrap" when they get to the top or bottom of the screen. So the y-position of the turtles is kept in a new variable (YPOS), and the turtle is hidden if its y-position moves outside the boundary of the screen. At each iteration of GO, each turtle looks at its neighbors and calculates a new speed and position accordingly. The order in which this is done is not obvious, since the turtles are running in parallel. It's important that the order in which the turtles look at their neighbors doesn't matter. Therefore temporary variables are created, "ypos-old", and "yvel-old". Each turtle looks at its neighbors in previous state and updates its own temporary variables "ypos-new" and "yvel-new". Then all the turtles update their states together. A TRUE STORY ------------ The programmer was asked by an undergraduate student to help her with some physics experiment problems. This experiment is about wave propagation and interference, two speakers are put on a streight track one meter apart and facing each other, the speakers are connected to a 1500 Hz sinusoidal signal generator, the student is asked to use a microphone to measure the sound level along the track between the two speakers and write down the positions where the microphone readings are minimum. The student is asked to explain the results and to determine if the minimum readings should be zero or not. The results show that the average distance betweeen two minumum readings is about one half of the wavelength. The programmer could not explain the results and determine if the readings should be zero or not though he knew it's about wave propagation and interference. StarLogo sample rope helped him to answer or verify the questions in the rope model, one end of the rope is fixed, he just changed this fixed point to a drive force, so this setup is the same as the experiment setup except the length and the frequency, he also changed one command that the y coordinate represents the absolute value of the deflection, because the microphone reading is root mean square value of the sound level. Run the program and it's very clear that the minimum readings should be zero and the distance between any two minima is one half of the wave length. Isn't it amazing, such simple program can be so helpful. Try and repeat what the programmer did and answer the physical experiment problems.