
|

|

|
Emergent Entities and Emergent Processes: Constructing Emergence through Multi-Agent Programming
Uri Wilensky
Northwestern University
uri@northwestern.edu
Paper presented at the Annual Conference of the American Educational Research Association, Seattle, WA: April 13, 2001
An expanded version of this paper is in progress. Wilensky, U., Hazzard. E. & Longenecker, S. (in preparation). A Bale of Turtles: A Case study of a middle school science class studying complexity through multi-agent modeling

|

|

|
1.0 Introduction
The debates of the 1980s about the nature of computer programming, the difficulties of children in learning to program and the proper role for programming in education have largely subsided. In the minds of� some, the question is resolved: 1) programming is too difficult for most kids, 2) it does not confer any special learning benefits, and 3) it is not necessary for realizing the educational potential of digital technologies. As a result of this "anti-programming" view (e.g., Pea & Kurland, 1984), during a time when the density of computers in the classroom has significantly increased and computer literacy classes have proliferated in schools, there has been a decline in the numbers of students engaged in programming computers.
However, despite the mainstream acceptance of the anti-programming view, a community of researchers has continued to study learning opportunities in programming and has authored a wealth of new programming languages and environments designed to enable children to be designers, authors and creators of computational texts. This community has steadily accumulated research suggesting significant benefits from students learning through programming. (e.g., Clements, 1999; diSessa, 2000; Noss & Hoyles, 1996; Wilensky, 1995). This new research and development has altered the terms of the programming debate and suggests a need to renew the debate in the new context.
In this paper, we focus on one key development in programming language design that should be a part of renewed discussion on learning through programming. There are now new programming languages for more specialized purposes -- languages that include in their basic ontologies objects and primitives that are tuned for a knowledge domain. Included in this category are the multi-agent modeling languages StarLogo/T (Resnick, 1994; Wilensky, 1995) and NetLogo (Wilensky, 1999; Wilensky & Stroup, 2000) employed in this study, which focus attention on systems and emergent phenomena. The image of computer programming as manipulating arcane symbols far removed from the relevant content domain has given way to domain rich tools in which language primitives are closely matched, epistemologically, to the domain of knowledge.
We present the results of research conducted in an eighth grade science classroom using such new epistemologically enriched programming languages -- the multi-agent languages StarLogoT and NetLogo. A curricular intervention, called EMERGE, was conducted in this classroom in 21 class sessions over a three month period. The curriculum integrated programming and modeling using multi-agent modeling languages with the study of complexity, parallel processes and emergent phenomena.
We believe the data presented in this paper counts as compelling evidence against the three negative claims mentioned above that characterize the anti-programming view. It is worth foreshadowing at the outset some results in this paper as they bear on student programming: 1) all of the middle school students in this study were able to write sophisticated computer programs in a language which they learned in relatively short order 2) the programming activities led to marked gains in understanding about the topics of complexity, parallelism and emergent phenomena and 3) the programming activities were integral to the development of understanding. That is, student understanding developed in conjunction with writing code for emergent behaviors. Student explanations of their understandings of the emergent phenomena were mediated and expressed through programming language objects, constructs and primitives. Exposure to the visual output of the simulations without the ability to construct and modify simulations did not result in such enhanced language and explanations.
In the remainder of this paper, we start by describing the domain of knowledge embedded in the EMERGE curriculum and then present and analyze two vignettes from the data we collected.
The goal of the EMERGE curriculum is to enable student to understand the global patterns that they observe — that is both to help them see more such patterns as well as classify them and understand how they arise. Before describing the results of our study, it is useful to step back and describe the fundamental concepts of emergent patterns and why they are difficult to discern and comprehend.
Mathematics as a discipline has been described as the science of patterns in general (Steen, 1986). Science is charged with classifying and explaining the patterns that manifest themselves in our natural and social worlds. Why is there so much observable pattern in the world? We can start with a simple observation: large scale patterns in the world are usually the result of the interactions of large numbers of smaller pieces that somehow combine in surprising ways to create the large-scale pattern. Such large-scale (macro-) patterns that arise out of the interactions of numerous interacting (micro-) "agents" are called "emergent phenomena" - that is, phenomena that emerge from interactions at a lower level or scale. Emergent phenomena, almost by definition, exhibit a counter-intuitive flavor. The reason the phenomena are labeled "emergent" is that it is quite difficult for us to predict how these global patterns will develop simply by observing the individual elements. For complex patterns, computational power is necessary for understanding the shape of development.
As the components of a system interact, they can form a pattern that is stable over time. We call such patterns emergent objects or entities (Langton, 1993; Kauffman, 1995). They emerge from the interactions of objects at a lower level or scale. As an example, a school of fish is a pattern of fish that can be stable for some period of time. The school typically results from the accumulated interaction of large numbers of fish (and other environmental and biotic conditions). Note that the school is not a simple accumulation or fixed collection of fish; in fact, fish are regularly exiting the school both temporarily and permanently and new fish are entering both temporarily and permanently. Such a school is an emergent entity. At first glance, it might seem that such emergent entities are rare birds, but if we look through the lenses of our emergent binoculars, we begin to catch the wings of emergent entities everywhere we turn. Flocks of birds emerge from the interactions of individual birds, and so it is for most congregations of animals, whether they be, colonies of ants or stampedes of caribou. But emergence is not confined to the biological world: prices emerge from the accumulated interactions of buyers and sellers; physical objects emerge from the accumulated interactions of particles; even our very selves are emergent, with cells sloughing off and being born into the ‘schools’ of our bodies. It thus becomes clear that almost all entities can be seen as emergent, it is a matter of adopting the emergent perspective and seeing the entity as a composite — an ensemble of interacting components. From this perspective, all entities can be seen as special cases of processes — processes that are maintained in a dynamic equilibrium.
Most patterns that arise in the world, arise out of the interactions of many components all moving at the same time — that is, they act in parallel. However, the formalisms that have been developed in mathematics and computer science to describe worldly phenomena obscure the parallelism since they describe change as happening one step after another -- a serial process. Computer science, burdened with the legacy of the Von Neuman machine, has been a particular culprit in converting parallelism in the world into serial algorithms. More recently, computer scientists have begun to explore parallel algorithms, but they have done so primarily with the goal of speeding up the execution of algorithms, not of helping us to think better about parallel processes themselves. Indeed, it is the explicit goal of designers to parallelize compilers to make the computer do the parallel part, so people do not have to think about it. This design practice seems to be supported by research (e.g., Wilensky, 1997) showing the difficulties people have in thinking about the details of how parallel processes can interact. But in an educational context, surely our goals are to help students make sense of the world’s complexity . And, in order to make sense of the systems of interactions that comprise a complex system, we need to better understand how multiple processes executing simultaneously can coordinate and result in a composite pattern.
Typically, the word "random" is used to describe a destructive process, one that does not have any reason or pattern. Yet randomness can be quite constructive — generating many of the beautiful patterns we see in nature such as the shape of a snowflake, the perimeter of a maple leaf, or the scarp of a dramatic cliff. All of these patterns emerge from the interactions of many tiny components governed by the laws of chance. Indeed, it is because of the tiny random "imperfections" in the snowflake crystal that we are fortunate to have such an astounding variety and beauty of snowflakes.
There is considerable research (Tversky & Kahneman, 1971; 1974; 1982 Nisbett, 1980; 1983; Konold, 1989; 1991; Evans, 1993; Wilensky, 1993; 1995; 1997) documenting the difficulties people have in reasoning about randomness and probability. Much of this research has focused on giving people mathematical problems in which they must calculate probabilities and examining the misconceptions that lead them to calculate these incorrectly. Little of the research has examined the epistemological beliefs that underlie difficulties with probability — in particular the conception of randomness as destructive rather than a major force to constructing stability, order and beauty in the world.
The accumulated difficulties people have in reasoning about parallelism and probability result in an emergent entity or pattern, we have called the "deterministic/centralized mindset" (Resnick & Wilensky, 1995; Wilensky & Resnick, 1999). This mindset causes people to see worldly phenomena as orchestrated and determined instead of as emergent. It focuses our attention at a single level of description rather than pointing us to the connections amongst levels. Elsewhere we have argued that a majority of us have this mindset, which powerfully constrains our perception of pattern When asked to explain an emergent pattern, we describe a leader bird orchestrating the formation, or a queen ant taking charge of the ant colony organization, or an accident ahead causing the formation of a traffic jam.
In previous work (Wilensky, 1997; 1999; in press; Resnick & Wilensky, 1998; Wilensky & Resnick, 1999), we have described how a deterministic/ centralized mindset might arise from our experience as active planning and designing agents in the world. Yet most of the natural world is composed of agents with much smaller capacities- agents that do not have enough neuronal capacity to conceive of a plan or enough bandwidth to communicate it to conspecifics. For agents such as these, the only "strategy" is to pool their capacities so that the interactions of the individuals create an ensemble pattern. Because of our experience as agents and our inability to attend to large numbers of factors or long periods of time, we do not have significant opportunities to develop robust intuitions about how emergent phenomena arise and maintain themselves.
In this regard, computational technology can be a powerful aid. By enabling us to create simulation environments in which we can experiment with and attend to large numbers of objects or agents in a reliable and replicable manner, computational environments can help us gain the experience that enables the construction of robust and sophisticated intuitions about emergent and the dynamics of complex systems changing over time. In the next section, we describe the multi-agent modeling languages which are designed to enable learners to accomplish this goal.
3.0 Multi-agent modeling languages
StarLogoT (Wilensky, 1997) and NetLogo (Wilensky, 1999) are multi-agent modeling language (aka agent-based or object-based parallel) designed to help learners explore and construct models of complex phenomena. These two languages are descendants of a lineage of StarLogo (Resnick, 1994; Wilensky, 1995; Wilensky & Resnick, 1999) languages that grew out of the Logo programming language. In Logo, children control a graphical turtle by giving it commands such as "forward", "back", "right" and "left" which causes the turtle to move and draw as it moves. In multi-agent languages, there are thousands of turtles or "agents". When they are given commands such as "forward" all the turtles on the screen (or the ones selected) move forward. Due to the movement in parallel of thousands of independent, distributed agents, mulatto-agent languages are well suited for the exploration of parallel process and the emergent phenomena that result from the enactment of these parallel processes. Users can write short programs that create turtle agents and cause them to enact specified behaviors. Besides turtles, these languages allow users to create their own breeds of agents, so users can control thousands of individuals on the screen whether they be cars in traffic, sheep in a herd, particles in a gas, or traders in a commodities market. It is important to note that both StarLogoT and NetLogo also support a special breed of agent, called a "patch". Patches are agents that do not move, they stay in a fixed grid filling the graphics screen. These special patch agents serve to model the environment, whether it be the lanes of traffic, the meadow in which the sheep are grazing, the box containing the gas or the commodities marketplace.
4.0 Project setting
The research reported on in this paper was conducted in an eighth grade science classroom at a small independent, Jewish-affiliated K-8 school located in the northeast United States. The student body is predominantly suburban and white, although around 20% of the students have backgrounds of relatively recent emigration to the United States from Russia. Student scores on the Educational Records Bureau’s (ERB) CPT3 test indicate the student body is comparable to suburban schools (defined by ERB) nationwide in quantitative and verbal aptitude.
The eighth grade class contained 12 students. Three students had diagnosed learning disabilities. ERB scores in the spring of 2000 showed the class’s quantitative aptitude ranged from the 19th to the 99th percentile compared to suburban schools nationwide (with a median percentile of 68). Its verbal aptitude ranged from the 23rd to the 99th percentile (with a median percentile of 67). Students’ names (pseudonyms) are used throughout the story to help it flow more easily.
The teacher, Steve, in his fourth year of teaching, had been the class’s science teacher since they entered sixth grade. He became familiar with StarLogoT and the ideas of complexity during an independent-study graduate course at Tufts University, in which he had written several StarLogoT models. In 1998 & 1999, he taught StarLogoT programming in a one period per week elective course. For the duration of this unit, a project staff member, Ed, worked with the teacher and interviewed students about their thinking about complexity.
For the project reported on herein, the teacher co-developed (with project staff) a special unit for his class. The unit employed StarLogoT and NetLogo as representational tools to focus on the ideas of complexity, parallel processes and emergent phenomena. This complexity unit (aka EMERGE) took place during the spring of 2000 in the science course of the school’s single eighth grade class. The class met for four periods (or 3.5 hours) per week, but because the unit was frequently interrupted (by the annual science fair, field trips, and school vacations), the 21 class periods devoted to it were spread out over three months.
The research site was selected for the familiarity of the teacher with the multi-agent modeling language and willingness of the teacher and the school to devote one month of class activity to the EMERGE unit. This classroom is clearly not typical of eighth grade science classrooms. Our goal here, however, was not to describe typical results, but rather to examine what is possible to achieve in both understanding and tool use with these new materials and modeling languages.
5.0 The EMERGE unit emerges — Pre-interviews
Now that we have described the EMERGE curriculum and school setting, we describe and discuss a few vignettes that illustrate the development of student understanding of the content domain.
Prior to beginning the unit, five students were interviewed about their understanding of emergent phenomena. Interviews lasted about thirty minutes and were videotaped and subsequently transcribed. Interview questions fell into three basic types: requests to reason about and explain worldly phenomena that could be described as emergent; Requests to describe and explain the workings of multi-agent simulations presented at the interview; and questions about statistical and probabilistic reasoning. Examples of topics covered in the interviews include reasoning about the origins and causes of traffic jams, the flocking and herding behavior of animals and the dynamics of a predator/prey ecosystem.
5.1 How do geese flock?
One pre-interview question concerned the formation of flocks of geese. The intent was to try and understand how the students conceived of the formation of the geese flock pattern. Would they think about it as an emergent pattern? Or would they think about it as a pattern deliberately orchestrated by a leader?
In general, the students conceived of the pattern as orchestrated. In each interview, the student described a leader goose being chosen in some fashion, and that choice resulting in the other geese serially falling into formation. None of the students described the geese as leaderless, or as all following the same rules of behavior. None described an individual goose’s flight as having a random component nor did they describe the geese as moving in parallel so that they simultaneously form into a V-shaped flock. Here are three rather typical examples:
Minnie
Minnie: I think the leader of them is the mother so this is her right here, then behind her and then it always ends up that there is about two or one at the back. I think the smallest one.
Ed: How do you think they know how to get in that order?
Minnie: I think they just follow their mother. I think that’s how it ends up being.
Ed: So you think when it’s a flock it might actually be a family?
Minnie: Yeah.
Alan
Ed: Suppose there is an instinct to go into a formation. You have a bunch of birds, they are all flopping around. How would you picture them knowing what to do, so to speak?
Alan: By size, the biggest one in front. Again it could be and so OK they find out that the V formation is more efficient than no formation so then they find that when the birds are arranged this way with the biggest in front and the smallest at the two ends of the V.
Andy
Ed: How do you think they get into that pattern?
Andy: Maybe geese talk. I don’t know.
Ed: Could be. They certainly talk.
Andy: They could communicate some way and designate a leader. They could have instincts in their brain. When they see the leader, they follow it. You can choose to be a leader sometimes unless there is not one. Like if you are just flying around, they have to have some information, so if brain or genes or something probably tell them, you go to the front and then every one else will follow
When asked to describe the formation of a flock of birds, the students naturally described the formation as a serial process. First one bird found "it’s place", then the next, and so on. They did not describe the birds as all finding "their place" at once. Of course, the whole notion of a "place" for a bird is itself suspect and tied to a serial conception. To organize the seriality of the assembly, the students needed some kind of leader bird — one bird that is designated as the orchestrator of the seriality (or if not a leader bird, an organizing principle). Whether it be a mother bird, the biggest bird or a bird "randomly" selected by its genes, the leader bird initiates the organization of the flock. The leader bird, having a distinct role from the follower birds, is thus seen to be following different rules than the other birds follow. The conception of the flock as an emergent entity, a pattern that results from the parallel movement of all its member birds following the same rules, is not manifested in any of the pre-interviews.
6.0 Beginning the Unit — constructing simple emergent models
After all pre-interviews were conducted, Steve began the EMERGE unit. We now move to describing two vignettes of what transpired in the classroom during the EMERGE unit.
During the first few weeks of the unit, the students constructed and explored several very simple multi-agent models of emergent phenomena. They learned to program in StarLogoT through writing several such models often models consisting of a single line of code. After writing a simple such model, Steve would ask the students to write down in their "lab notes" a prediction of what they would see and then after running the model, what they observed. In Steve’s class, this procedure was relatively informal. Due to limitations in data collection we do not have copies of these lab notes. However, in a subsequent implementation of an EMERGE unit, the procedure became a bit more formalized and students and teachers came to describe these exercises as the POLE (Predict, Observe Levels, Explain) method. Initially, they used a three-column format in their lab notes and made many such "experiments" over the first few class sessions.)
A typical early entry in the lab notes came from Maude:
Command: fd random 30
Prediction, the turtles will show up in a circle with a radius less than 30
Observation: the turtles aren’t in a circle, they’re spread out in a cloud. There are more near the center than at the edges.
Explanation: Maybe they want to stay warm? Sorry. I couldn’t resist. Each turtle is going a different distance. I guess maybe each turtle could be doing a different random.
In the more formalized setting, the teacher suggested they expand the categories of their lab notes to describe the global pattern as well as the turtle behavior. He suggested they do this by splitting the observation column in two, the turtle level and the observer level. Helen’s first such entry:
Command: fd 25
Prediction: the turtles are in a circle 25 units big
Observation:
Turtle Level: Each turtle moves forward 25 units
Observer Level: The observer sees a circle on the screen
Explanation: the turtles started out with different headings and went the same distance, so the observer observes a circle.
7.0 Olga describes emergent phenomena
After exploring many such simple models, for homework, Steve then asked the students to write a paragraph describing the concept of emergent phenomena.
Olga’s comments below indicate that her understanding of emergent phenomena is closely tied to the multi-agent language representation.
"StarLogoT phenomena can be described at two different levels: the ‘turtle’ and the ‘observer’ level. This means that when the turtle is doing one thing it looks like something else to the observer. They have different views and therefore, it seems like they are doing different things. For example: when you create 50 turtles and have them go forward 20 spaces, all the turtle’s doing is taking 20 steps forward, but to the observer it looks like a bunch of turtles in a circle. When you have 2 liquids (milk and juice), you have a bunch of molecules jumping and vibrating, and to them all they are doing is vibrating because of their neighbors and that is why they are so solid. When you pour some juice into a glass, all you see is juice being poured from the container, but the molecules feel and see all their neighbors moving around and vibrating."
At this point, the class had had a number of discussions about the way in which one’s perspective affects how one views a phenomenon. The vocabulary of turtle level and observer level was familiar to the students and, as Olga’s paragraph suggests, they were comfortable with these ideas. StarLogoT played an important role in helping students form this initial conception of emergent objects. We see this in Olga’s use of the classic example of individual turtles forming a circle (which she had tried herself earlier) in her initial discussion of emergence. The natural mapping between the StarLogoT graphics screen and the world of objects (in other comments, she imagines being a turtle or a helicopter above the turtles) helps Olga to picture the liquid as a cloud of vibrating turtles.
Olga then uses StarLogoT as a bridging analogy to an instance of emergent phenomena from real life -- the case of molecules forming a liquid. Just as turtles moving 20 steps forward can form a circle, molecules "jumping and vibrating" can form a liquid. In both cases, the agents aren’t aware of their membership in the entity, nor of how the entity is constituted from their actions.
This example points to the growing sophistication of Olga’s thinking. She is clearly struck by the apparent paradox of the "solidness" of the individual objects (as Olga understands molecules) and the "liquidness" of the resulting emergent object. It is an important development in student understanding of emergent phenomena that they recognize the degree to which the properties of emergent objects can differ from the properties of their constituent parts (see Wilensky & Resnick, 1999).
At the same time, Olga’s writing reflects only an initial understanding of emergent entities. Her examples suggest that she thinks of "levels" principally as a simple change of scale, resulting in a difference of perception. In the first example of the paragraph, she states this explicitly: "they have different views and therefore, it seems like they are doing different things." The same thing is implied in the second example: "all you see is juice" vs. "the molecules feel and see all their neighbors moving". Olga hasn't yet tackled the causal relationship between molecules and liquid. Indeed, this is a central puzzle for young students in beginning chemistry classes: how does one reconcile the properties of the individual particles making up a substance and the differing properties of the substance itself?
There is a tentative exploration of which perspective is more "correct". When Olga writes, "all you see is juice," there is a slight implication that what's really there is "a collection of molecules." Also, in both of these examples, constituent membership in an emergent object is static: the liquid, however it moves, is always the same collection of molecules. It doesn’t have an independent existence, as a wave might be thought to have. Only later do students come to see emergent entities as having an existence independent of their constituent parts and actively engage in the question of which level is more "real".
8.0 What is a Population?
In the next class, students worked in pairs to make a simple population model. The project description introduced several new commands and components of the language such as sliders (and therefore, indirectly, variables), the hatch command, and the die command. Students explored how different slider values for a hatchingchance variable and dyingchance variable affected how quickly the population grew. Students were asked to predict what their models would do prior to running them and they kept "lab notes" on the results of their "experiments". It took two class periods to finish this project.
The following week, the students discussed their observations of the simple population models they had produced. Steve introduced the distinction between global and turtle variables, the former being the same for everybody (such as slider variables), and the latter being different for each turtle, such as heading and color. With these additional tools, they worked with their partners to extend the simple population model and make it more realistic in some way of their own choosing.
After two class periods of intense programming, the students presented their models to each other. Each of the four models presented was unique.
a) One used the turtles’ colors to represent their life cycle stages. Turtles were blue at birth and stayed blue through a non-reproductive youth (until age 18 ticks). Then they turned red, and at each tick there was a chance (controlled by a slider variable) of reproduction. Finally, at age 60 ticks, turtles turned green, could no longer reproduce, and had a chance each tick (controlled by another slider) of dying. The discussion centered on the fluctuations in the sizes of these three age groups.
b) Another model used color to indicate how old the turtle’s parent was when it was born, so that red turtles had been born to a "middle-aged" parent, while blue turtles had been born to an "old" parent.
c) The three girls in the class presented a model in which turtles reproduced constantly once they were 12 ticks old and died automatically when they were 80 ticks old.
d) Bruce and Zach made a model in which they chose low, balanced birth and death rates to keep their population low. Turtles had the same color as their parents. We now give this last model additional attention.
9.0 Bruce and Zach’s population model
Model summary: Create 20 differently colored turtles. Set the clock to 0. With each tick, each turtles has a 0 to 100% chance of hatching one other turtle, and an independent 0 to 100% chance of dying. The clock increases by 1. Age has no effect. If each of these chances is set at 1%, the population always eventually dies out. For example, in the run shown in Figures 1a and 1b, only two gray turtles are left after 4000 clock ticks.
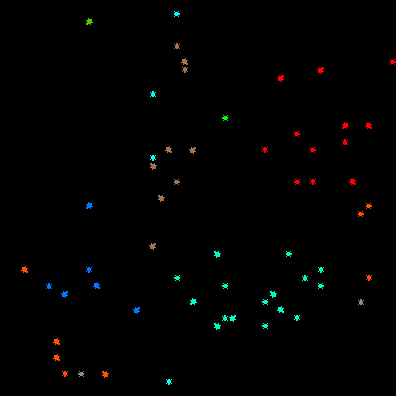

Figure 1a: Expanding population Figure 1b: Two turtles left
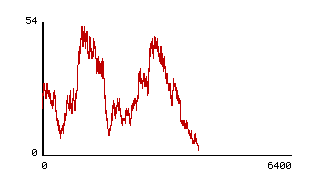
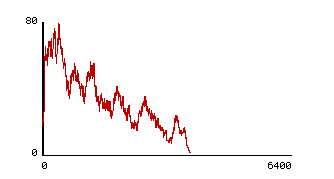
Figure 2: Two population plots from runs of the model
Bruce: Do you see how much variance [in the population] there is over time [pointing to the plot window of the total population — Figure 2] in increases and decreases? So, sometimes our model will [die] within 100 or 200 ticks but sometimes [the population] will get up past a 100 turtles. Simply depending on ...
Zach: and here it seems like 60 is pretty constant for our population and that’s ...-
Bruce: I don’t think there is a constant actually.
Zach: [considering agreement] well it shows some variation.
Steve: let’s say you get up to a hundred, does that mean you’re likely to not ever die out because, because you have so many turtles?
Bruce: Well, let’s try it. Let’s run the model starting out with 100 turtles…
Bruce and Zach changed the model so that it started out with 100 turtles. They also made it run faster so that the results could be seen more quickly. The class found out that the population could still die out. There was discussion of what the birth rate was and whether birth rates and death rates are equal. Bruce and Zach said they’d tried to make the chance of reproducing over the entire reproductive period exactly one, but they thought it was slightly less than that.
These experiments were repeated a number of times and discussion began to break down into small groups looking at different aspects of the model. One student, Helen, noticed again that each time the model ran, a differently colored group of turtles came to dominate the graphics window.
Helen (to Steve): Why does each time… why does only one color end up on the screen? [see Figure 1b]
Steve (to the class as a whole to bring it back to order): Umm, why is there only one color? Because by random chance, look at all those colors there are [pointing to the screen when the model is just beginning]--
Zach (interrupting): There’s twenty [colors].
Steve: Each turtle, when it hatches, it hatches a baby that is the same color as its parent?
Helen: yeah.
Steve: So if you happen to have the other colors die out, then you can’t get… it’s like extinct. You can’t get…
Helen: but why?
Zach: So okay, I’ll show you. By random chance, one color… it’s just… it’s gonna be one color because…
Helen: Why?
[a little laughter from others… this is a hard question]
Zach: So say a red turtle hatches another red. They…
Helen: Another green hatches another green.
Zach: But say, by probability they die out, so now we have nineteen [colors]--
Helen: You have a probability for when they [a color] will die?
Bruce: No, Helen, what we are saying is… let me try to explain… this is something that you should have observed in one of the worksheets we did. Suppose that in the first ten turns, or in the first twenty turns, the red turtles have three babies. Unlikely, but possible, right? Then the red "race" — their probability of giving birth is four times everyone else’s, so they’re more likely to grow. And the green turtle has a high probability of just dying, right? So by probability it usually ends up at one of the colors. It’s not that red always takes it.
Zach: It’s that a color takes it.
9.1 Surprising instabilities
In this vignette, students are exploring the issue of stability�. While programming the model, Bruce and Zach had expressed a desire to find local rules that produced a stable population, but when they ran the program it was hard for them to tell if it was stable or not. � Zach was looking for and probably thought there should be an underlying constancy. Bruce seemed to be comfortable with a less predictable outcome. The students were open to the teacher’s suggestion that initial size may have an impact on population stability, but this turned out not to be a simple relationship, as it had been with clouds of random-walking turtles in an earlier exploration. �
Helen’s insightful query raises a different randomness vs. determinacy question. The students are struggling to understand why, if all the individual turtles have an equal chance of reproducing, only one original turtle’s progeny are eventually left on the screen. The inevitableness of the pattern is quite puzzling to them. When Helen asks whether the model contains a probability for a color to die out, she’s quite reasonably looking for a global rule to explain this general result. This illustrates a place in which students are having trouble separating the turtle and observer levels and seeing how local rules connect to emergent phenomena and produce counter-intuitive results. Without intending to, Bruce and Zach have produced a model that illustrates surprising aspects of evolutionary theory concerning genetic drift, extinction, and population bottlenecks. They gained considerable insight by exploring this model in the lab before their presentation, and they made a valiant effort to explain it to the class. {Technically, they are incorrect when they say that the red turtles have a better chance of growing…}
The use of the modeling language makes it possible for these students to explore a content area that is difficult for even advanced (undergraduate) students to understand, precisely because the difficulty lies in bridging one level to another.
In exploring these models, Bruce and Zach were also exploring exponential growth — any situation where how many more depends on how many there already are. Earlier on the students had explored the growth of a single population and saw how their populations took off, gaining an intuitive understanding of the exponential math without the symbolic representation. In the model described in the vignette, the students are exploring a model that has both birth and death. Both of these processes behave exponentially, so the combination is not easily predictable. The students were looking for a stable situation, and one significant discovery they made was that it was hard too find.
10.0 The Younging of America
Upon returning from a two-week vacation for Passover, Steve reviewed the work done so far and discussed the larger ideas about complexity. He also introduced the class to the next project and introduced some new StarLogoT coding techniques.
For homework, Steve asked each student to read an article (Hayes, 1999) about StarLogo and to write a paragraph explaining how the population model they made fit the article’s description of, "phenomena that emerge from the interactions of many individual things."
The following day they discussed the article in class. Students were having trouble with the homework assignment since in their minds the turtles in their population models didn’t interact. Steve admitted the word "interaction" was difficult, but that one could still talk about population as a different kind of entity than merely a bunch of turtles.
Steve: Brad and Ira. So, maybe you could talk about the population getting older over time. You’re observing the population. It’s a separate thing from all the different turtles. Every turtle’s getting older every turn step, that’s true. But the whole population is getting older if you’re going from having a bunch of young turtles everywhere to a bunch of old turtles everywhere. They talk about maybe the "graying of America." Have you ever heard that phrase?
[class gives noncommittal affirmation]
Steve: The "graying of America" is something you’ll see more and more of, I bet. Because what they mean is that the average age of the population of the United States is getting older. Why would that be? Why would the average age…
Bruce: Good health care?
Steve: Good health care. Partly.
Brad: People are living longer.
Helen: People are having less children?
Steve: People are having less children!
Brad: Living longer.
Steve: And people are living longer!
Olga: And a lot of young people are dying.
Steve: And a lot of young people are what?
Olga: [serious] A lot of young people are dying.
Steve: Could be. I don’t think that’s — I’m not sure that’s what’s happening.
Bruce: I don’t think people are having less children either. I think it’s just the, also the baby boom.
Steve: And the baby boom. There seems to be a lot of people of a certain age, and that group of people is getting older. And there’s so many of them compared to maybe those of us in my generation and your generation that that’s overwhelming.
Andy: So that can easily change in thirty years.
Steve: Sure, maybe in thirty years we’re going to have a big…
Doug: A big drop.
Andy: The "younging of America."
Steve: Yeah, America is getting younger. But does that mean that you’re getting younger? No. But it means that the average age of the population… maybe there’s more kids and so things like, suddenly MTV ratings are getting higher and higher and — what would be getting less popular?
Dan: C-Span.
Bruce: VH-1.
Steve: C-Span and VH-1, you know, are losing popularity because America is getting younger.
Zach: All of that are entered the baby boom, you know, there’ll be a year where tons of people from one year… you know there’s going to be a year where there’s more death eventually.
Bruce: But it’ll become more spread out eventually.
Steve: So this can fluctuate.
Zach: More births, more deaths.
Steve: And we might get to a point where we might say suddenly, "you know what, America’s staying the same age."
[class laughs]
10.1 Individuals and aggregates
In a post-interview, Steve cited the above dialogue as one of the principal turning points for the class in terms of truly understanding the meaning of turtle and observer levels. The class understanding at this point is a significant advance beyond the perspective expressed in the paragraph written by Olga in which she says observer and turtle views "look" different. In this discussion, students are able to understand the apparent paradox that a population can get younger while every individual in the population gets older. Students are see the population as a distinct entity, while understanding that this entity is actually composed of individual pieces at another level.
In this case, the "entity" -- the US population — was less a physical object (like a liquid) and more an abstract thing, with a rather mathematical characteristic, namely an age distribution. Making an analytical connection between individual ages and the aggregate age of the whole was one more step forward for the students in being aware of two levels simultaneously and constructing a relationship between them. Only then could they conceptualize a causal relationship between the local rules and the emergent aggregate. Furthermore, the situation was dynamic; as individual rules and histories changed, so did the aggregate distribution. The students appeared to be comfortable with, and perhaps even excited about, this fluid and dramatic situation.
There is also evidence in this discussion of a much stronger understanding of the interaction between local rules and emergent/global patterns than the students had shown in previous discussions. Grounded in a familiar context within which they had significant modeling experience, students found it easy to understand the connection between a lengthening life span (due perhaps to better health care) for each individual and a growing average age for the entire population. Although there is actually no explicit mention of StarLogoT during the discussion beyond the opening lines, the students were well aware of the connection between a rule (fewer children) and the corresponding rule in StarLogoT (lower hatching chance). In a post-interview, Steve, described it well:
"The various programming experiences the students had creating local rules and observing emergent population dynamics was vital to the students’ comfort (and even good humor) with the ideas they articulated about populations and emergent phenomena in general. The idea of the observer and turtle level provided a grounding metaphor as well as a technical language for describing such phenomena."
11.0 Conclusion
In this middle school science classroom, all students were able to progress in a relatively short amount of time from building simple multi-agent models to more sophisticated models that engaged the class in extended inquiry activities. At the same time, their sophistication in describing emergent phenomena, levels of organization and description, randomness and variability as well as traditional population dynamics showed marked gains. How are we to interpret these rapid learning gains in subject areas that have been regarded as difficult and resistant to tuition? Our conjecture is that learning the programming language together with the subject matter was an easier task than learning either alone. Opponents of the use of programming in school classrooms have often argued that the overhead associated with learning the language distracts students from the material to be covered. It would thus appear that learning content through programming imposes too high a cost on content coverage and understanding. This argument, however, rests on an assumption of "linearity". To characterize the argument in algebraic terms, we could say: If the time to learn population dynamics is "x" and the time to learn StarLogoT is "y", then the time to learn them both is "x + y" a seemingly unacceptable cost, unless y is very small. The results presented herein suggest that this linear model is wrong. A programming language that is characterized by epistemological commitments that support the domain of inquiry, can make the time to learn both the language and the domain smaller than either "x" or "y" alone. For students of complex systems and emergent phenomena, this is not a surprising result. Indeed, the norm in a complex system is that interaction amongst its components can make the systems behave in ways that are very different than the "sum of their parts".
Acknowledgements
The research described in this paper was supported by a post-doctoral fellowship from the Spencer Foundation and the National Academy of Education. The development of the StarLogoT and NetLogo modeling languages and many of the curricular materials was supported by the National Science Foundation under grants REC-9632612 and REC-9816482. Ed Hazzard, CCL Curriculum Coordinator, and Stephen Longenecker, eighth grade science teacher, were invaluable collaborators in this research.
References
diSessa, A. A. (1997). Open toolsets: New ends and new means in learning
mathematics and science with computers. In E. Pehkonen (Ed.), Proceedings of the 21st Conference of the International Group for the Psychology of Mathematics Education, Vol. 1. Lahti, Finland, 47-62.
DiSessa, A., Hancock, C., Hoyles, C., Noss R., & Wilensky, U. (2001). Constructing Process: The Varieties of Programming Experience. Panel presentation at the American Educational Research Association Annual Meeting. Seattle, WA: April 13, 2001.
Hammer, D. (1994). Epistemological beliefs in introductory physics, Cognition and Instruction, 12 (2), 151-183.
Jackson, S., Krajcik, J., & Soloway, E. (1999). Model-It: A design retrospective. In Jacobson, M. and Kozma, R (Eds.), Advanced designs for the technologies of learning: Innovations in science and mathematics education. Erlbaum: Hillsdale, NJ.
Kauffman, S. (1995). At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford: Oxford University Press.
Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
Pea, R. & Kurland, D.M. (1984). On the cognitive effects of learning computer programming, New Ideas Psychol, 2 (2) 137-168.
Repenning, A. (2000). AgentSheets®: An interactive simulation environment with end-user programmable agents," Interaction 2000, Tokyo, Japan. [http://www.cs.colorado.edu/~ralex/papers/index.html].
Resnick, M. (1994) Turtles, termites, and traffic jams: Explorations in massively parallel microworlds. Cambridge, MA: MIT Press.
Resnick, M. & Wilensky, U. (1993). Beyond the Deterministic, Centralized Mindsets: New Thinking for New Sciences, Presentation at the annual meeting of the American Educational Research Association, Atlanta, Ga.
Resnick, M., & Wilensky, U. (1998). Diving into Complexity: Developing Probabilistic Decentralized Thinking Through Role-Playing Activities. Journal of the Learning Sciences, 7 (2), 153-171.
Steen, L. (1986). Living with a new Mathematical Species. Math Intell 8:2 33-49.
Wilensky, U. (1995). Paradox, programming and learning probability. Journal of Mathematical Behavior. Vol. 14, No. 2. p. 231-280. [/cm/papers/paradox/pplp/]
Wilensky, U. (1999). GasLab–an Extensible Modeling Toolkit for Exploring Micro- and Macro- Views of Gases. In Roberts, N., Feurzeig, W. & Hunter, B. (Eds.) Computer Modeling and Simulation in Science Education. Berlin: Springer Verlag.
Wilensky, U. & Reisman, K. (in press). Thinking like a wolf, a sheep or a firefly: Learning biology through constructing and testing computational theories. Cognition & Instruction.
Wilensky, U. & Resnick, M. (1999). Thinking in levels: A dynamic systems perspective to making sense of the world. Journal of Science Education and Technology. Vol. 8 No. 1. pp. 3 - 18. [/cm/papers/levels/levels.html]
Wilensky, U. & Resnick, M. (1995). New Thinking for New Sciences: Constructionist Approaches for Exploring Complexity. Presentation to the American Educational Research Association, San Francisco, CA.
Wilensky, U., Stroup, W. (2000) Networked gridlock: Students enacting complex dynamic phenomena with the HubNet architecture. Proceedings of the Fourth Annual International Conference of the Learning Sciences, Ann Arbor, MI, June 14 - 17, 2000.
[/cm/papers/gridlock/Wilensky-Stroup.html]