
|

|

|
A Hands-on Modeling Approach to Evolution: Learning about the Evolution of Cooperation and Altruism Through Multi-Agent Modeling - The EACH Project
Damon Centola, Uri Wilensky, Eamon Mckenzie
Center for Connected Learning & Computer-Based Modeling
Northwestern University, Evanston, IL 60208
Tel: 847-467-3818, Fax: 847-491-8999
Email:
damon@ccl.northwestern.edu, uriw@media.mit.edu, emckenzie@tufts.edu

|

|

|
Keywords: science education, modeling/models, learning environments, mathematics education
It is a premise of much of the work in evolutionary biology that cooperative and altruistic behaviors are at odds with the evolutionary success of individuals. When high school and undergraduate students learn about evolution in the classroom, the tacit (and explicit) assumptions encourage students to envision the evolutionary process as a competition among same-species individuals for reproductive success. In one sense, this understanding of evolution is productive — it gives students powerful conceptual tools for understanding adaptation. However, teaching evolutionary theory without giving students a sense of the central importance of social and environmental factors can promote misleading intuitions about how evolutionary processes work. An approach to teaching evolution that focuses solely on individual factors limits students’ abilities to understand the complex ways in which environmental and social factors bear on the evolutionary success of individuals. The "multi-level" approach to teaching about evolution allows students to conceptualize the issues on adaptation in a way that is both more consistent with recent developments in the research literature and more rooted in related student interests and experience.
Recent developments in the field of evolutionary biology (Axelrod, 1984; Wilson & Sober, 1998; Mitteldorf & Wilson, in press) have begun to expose aspects of complexity in the process of evolution that have substantially altered our basic intuitions about how group dynamics affect the genetic success of individuals. Specifically, there is good evidence that cooperative behavior may be a benefit to an individual’s evolutionary
success. Yet, many students who have been taught to think of individuals as discrete parts of an evolutionary system, have a difficult time understanding how cooperation, or altruistic behavior, could evolve. Because students’ intuitions about evolutionary theory have been based on a model of individual success that does not consider the complexity of natural systems, many have had a difficult time re-framing their understanding of evolution (Jacobson, 1996). The goal of project EACH (The Evolution of Altruistic and Cooperative Habits) was to develop sets of activities that would enable students to develop intuitions about the complex dynamics of individuals and groups in an evolutionary system.The Project Frame
The EACH project is one of many curricular interventions undertaken as part of the NSF funded "Making Sense of Complex Phenomena Project (MSCP)" (Wilensky, 1997a). The goal of this project is to build computer-based tools and curricula to enable students to explore and make sense of complex systems and to study student sense-making using these tools. As part of the MSCP project, we have developed the multi-agent modeling language StarLogoT (Wilensky, 1997b), in which all activities described below are written. StarLogoT is a computer modeling language designed explicitly for exploring systems with multiple interacting "agents". It is one of a new class of multi-agent (AKA object-based parallel) modeling languages. It is an extension of the StarLogo language (Resnick, 1994; Wilensky, 1996). StarLogoT is a parallel version of Logo and builds on the Logo metaphor of a "turtle". In traditional Logo, students create graphic images by giving commands to the turtle. In StarLogoT, students can give commands to hundreds or thousands of turtles, telling them how they should move and interact with one another. They can use StarLogoT turtles to represent many different types of "agents," such as flashing fireflies, cars in traffic or molecules in a gas. In addition, the graphics "background" is composed of "patches" which can be given commands in the same way as turtles except that they don’t move. The patches can thus be used to model an environment that contains a food supply, hills and valleys, or physical boundaries. Turtles and patches can affect each other; thus facilitating models in which figure and ground, organism and environment interact. Turtles and patches can act independently but can also be synchronized to the "ticking" of a global clock.
The latest version of StarLogoT and an associated collection of "extensible" models (collectively entitled "Connected Models" (Wilensky, 1998)) are available for download at ccl.northwestern.edu/cm. The models are drawn from a wide range of disciplines including physics, biology, mathematics, computer science, chemistry, materials science, ecology and economics.
The Context
The EACH project emerged out of the larger scale MSCP project (located at Tufts University’s Center for Connected Learning and Computer-Based Modeling (CCL). As part of the MSCP project, we studied students at many different grade levels as they explored and created models of complex phenomena in the language StarLogoT. Students (from middle school to graduate school) came to the CCL and met informally with project staff who mentored them in learning StarLogoT. Students explored models from the project library according to their
interests. They were encouraged to vary and extend the underlying StarLogoT code for the project sample models and, when they felt ready, to create new models from "scratch". The topic of evolution, in general, is one that has appealed to many of the student modelers. For the high school students and many of the undergraduates as well, evolution was studied largely in "story" form. That is, they learned stories of how the theory of evolution came into being, how it was resisted and how it is supposed to work. Many of the students found these stories intriguing but unsatisfying. The dissatisfaction consisted of feeling that they did not have an adequate methodology for testing the plausibility of particular evolutionary arguments or for evaluating competing evolutionary claims,Connected Learning
The EACH project is situated in a Connected Learning (1993; 1999) Framework . Connected Learning arises out of a constructionist (Papert 1980; 1991) paradigm that suggests that powerful learning arises from learners’ construction of artifacts and external representations. Connected Learning suggests that a particularly valuable feature of learner constructions is the richness of the web of connections (Wilensky, 1991; 1993) constructed. The Connected Learning Framework was first instantiated in the Connected Mathematics (Wilensky, 1993), Connected Probability (Wilensky, 1995) and ConnectedScience (Wilensky & Reisman, 1999) projects. In the EACH project, we used a developmental sequence of activities and constructions that has been used successively in these projects. Students advance their participation in the EACH project through several stages. In the first stage, they view a projected StarLogoT model of evolutionary strategies and engage in discussion of the outputs of the model. In the second stage, they explore the model on their own, varying parameters of the model and recording the outputs. In the third stage, they open up the glass box of the model code and make a revision to the underlying premises of the model. In the final stage, they create their own conceptual models and code them from "scratch" in StarLogoT. The StarLogoT modeling language affords a natural diving in (Resnick & Wilensky, 1998; Wilensky, 1997a) to the complexity of the phenomena through identification with the individual elements ("agents") of the model. The sequence of stages scaffolds a contextualized model-based inquiry -- students pose questions arising from their interactions with models and then mutually refine the questions and models
The Students
The students participating in the EACH project included undergraduate students at Tufts University. The students were primarily drawn from the humanities, the sciences, and engineering departments; they had all studied evolutionary theory in either a high school or university class.
When asked to discuss their ideas on evolutionary theory the students expressed the common intuitions about individual selection, all of them relying the catch-phrase "survival of the fittest." But when asked to flesh out the idea of fitness, the students had difficulty articulating what ‘fitness’ meant to them beyond the popular notion that fitness was strength: the power of an individual to dominate other individuals. These pre-session interviews gave useful guidance to the research team on how to scaffold student interaction with the models. They also served to set the ground for the project intervention as students started to question their assumptions about the meaning of "fitness" — questions which were elaborated and discussed once they began to interact with the models.
The Setting
The setting was informal and the activities were conducted in the research labs at the CCL. The students first discussed with us their background in evolutionary theory, and their intuitions about the evolution of altruistic and cooperative behaviors. Each student then explored the StarLogoT environment until s/he was comfortable with his/her understanding of turtle and patch agents. We then discussed the idea of emergent phenomena. All of the students were engaged in this inquiry, and a few immediately worked with us to develop simple models of collective behavior so that they would understand the concept of "emergence" in their own terms. Once the students were comfortable with StarLogoT, they began explorations of a set of models about the evolution of cooperation and altruism -- models designed specifically for the EACH project.
The Activities
An early goal for the EACH project was to develop a set of two seed" models in StarLogoT that , along with accompanying materials, would serve to expand the discussion in an evolution curriculum to include altruism and cooperation.
The first model we developed was a conservative model of evolutionary behavior based on current theory in evolutionary biology (Hamilton, 1964; Mitteldorf & Wilson, in press). This first model has two types of agents: selfish and altruistic. The premise of the model was that each agent would look around to its neighbors and see whether they were altruistic or selfish. For each altruistic neighbor, the agent increased its fitness by a fixed value. Thus, each agent with altruistic neighbors would have a higher fitness in the reproductive lottery. Each agent then calculated its fitness with one of the following equations:
If I am a selfish individual, my fitness is 1 + my benefit from my altruistic neighbors.
If I am an altruistic individual, my fitness is 1 — the cost of being an altruist + my benefit from my altruistic neighbors.
The values of ‘benefit’ and ‘cost’ were "slider"-variables that were set at values such that the cost of being an altruist significantly weakened the fitness value of altruists, while the benefit from the neighboring altruists were only significant when there were two or more of them.
Each agent is at the center of a five-agent neighborhood. To enter the reproductive lottery, each agent looks at its neighbors (in the four cardinal directions) and assesses their fitnesses. All of the altruistic agents’ fitnesses are summed (including the central agent, if it is an altruistic agent), and all of the selfish agents’ fitnesses are summed (including the central agent, if it is a selfish agent). These sums constitute the weight of altruistic ‘seeding,’ and the weight of selfish ‘seeding’, respectively, for the center spot in the reproductive lottery. To complete a generational cycle, a random number is picked between 0 and the total of the weights for a spot. The spot is then given to the type of agent whose weighted chance fell on the side of the random number. The higher an agent-type’s weight, the greater the chance that that type of agent will win the spot.
We included control parameters in the model, so that students could set the relative density of the altruistic and selfish populations. The clear outcome of this initial model is that the fitness of the selfish agents is higher than the fitness of the altruistic agents. Depending on the relative population densities, after about two-hundred generations (about thirty seconds), all of the altruistic agents are extinct; the upper bound on this time, starting with almost no selfish agents, is about five-hundred generations before the altruists are extinct. The outcome of this model fits well with standard adaptationist expectations of evolutionary theory (Hamilton, Williams, 1992) and sociobiology.
Figure 1a below is the control interface for the Altruism-Model 1. Figure 1b shows the model when it starts running. The pink agents are altruistic and the green are selfish. Figure 1c shows the model after it has run for about 100 generations (about thirty seconds running on a typical project iMac computer).
Altruism-Model 1
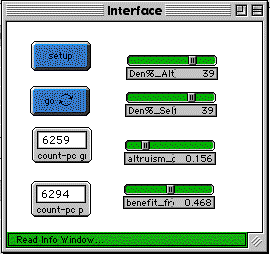 Fig. 1a |
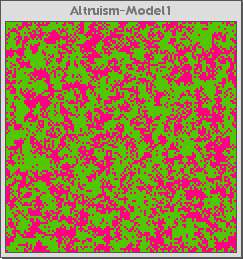 Fig 1b |
 Fig 1c |
The second model, based on recent work in the evolutionary biology of cooperation and altruistic behavior (Mitteldorf & Wilson, in press), introduces a new element to the model: adversity. The second model adds a slider-variable called ‘Harshness,’ and a slider variable called ‘Disease.’ The harshness variable gives each empty "patch" (a unit of the screen that is not occupied by a selfish agent or an altruistic agent) a chance of staying empty (resisting population) each turn. Envisioning the model-world as an environment in which individuals need to occupy a space on the grid in order to live, the harshness variable limits population growth by, at each clock "tick", making some of the spaces uninhabitable The disease variable is incorporated into the reproductive lottery for each spot. The value of this variable corresponds to the chance that an agent that occupies a spot on the grid will fail to reproduce, and thus that the spot will become empty. The introduction of these elements into the model alters the relationship between individuals and their environment. The new threats to the well-being of individuals reframe the importance of group behavior on individual success. This second model has a much richer parameter space -- students can explore the effects of the various harshness and disease values on the stability of the altruistic and selfish populations.
Figure 2a below is the control interface for the Altruism-Model 2. Figure 2b shows the model after thirty generations. Figure 2c shows the model after about two-hundred-fifty generations.
Altruism-Model 2
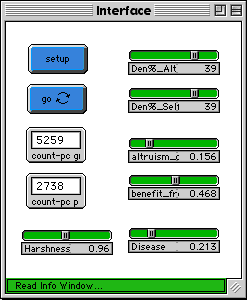 Fig. 2a |
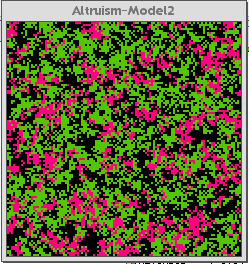 Fig. 2b |
 Fig. 2c |
Students found that when the harshness value is set around .96, and the disease value is set around .2, the model shows the surprising result that the altruistic population fares far better than the selfish population. Why should this be? This counter-intuitive result comes from the fact that when the natural conditions are harsh enough, single agents cannot survive against nature. That is to say, even though the selfish agents would fare better in competition against the altruistic agents, the altruistic agents would fare better against nature than the selfish agents. The reason for this is that altruistic agents survive in groups of altruists. Each altruist adds to the fitness of the other altruists. While a lone altruistic agent can survive no better than a lone selfish agent, because the altruists contribute to the well-being of the agents around them, the community can survive, with its combined altruistic benefit, in the face of harsh conditions.
The Reactions
In use with undergraduate students, the hands-on exploration of the model, discovering its dynamics for various parameter settings, successfully aroused new intuitions about the relationship between individual success and the importance of social and environmental considerations. The surprising success of an "altruistic strategy" encouraged students to question the model’s applicability to human behavior, and to explore the meaning of altruistic behavior in general.
At this point, the students themselves began wanting to develop models as a means of further refining their understanding of the potential fitness benefits of altruistic/cooperative behavior. As StarLogoT is a "glass-box" modeling language, they were able to "look under the hood" of the first two seed models and develop their own model extensions.
A New Understanding of Fitness
Ashley is a junior at Tufts University. She is a biology major, but her exposure to evolutionary theory was limited to introductory high school and college courses. She was interested in the EACH models because she wanted to understand whether and how biology could shed light on altruistic behavior. Initially, she saw the clear fitness benefit in being a selfish agent, and predicted that the selfish agents would run the altruists to extinction. After the first model, Ashley suggested exploring different settings of the Harshness and Disease variables. She predicted that, "the selfish agents will win again because they will have a higher fitness to protect them against the disease."
As we ran the second model, she first watched both populations decline, but then saw the altruistic population begin to grow, and finally to dominate the entire grid. She remarked:
"I thought the selfish agents would win, but they’re dying because they have less resistance to the disease. The altruists are benefiting one another, so they have a genetic resistance to the disease. The selfishists [as she called the selfish agents] don’t have any resistance, so they’re dying out….When there is a disease, the altruists are the stronger agents, even though they were weaker when there wasn’t one."
Ashley then turned the Harshness slider to 0, to see if disease alone could make the altruists win. It turned out that the selfish agents won out, even with a lot of disease. Ashley then noted that since the Harshness value is what kept the empty spots from being repopulated, that it this must play an important role in the survival of the altruists. She looked back at the first model, and then returned to the second one; after running the second model again, she exclaimed:
"Oh! I get it. The void spots are keeping the altruists from mingling with the selfishists. Because they’re separated, the altruists can give the benefit to each other without the selfishists leaching any of their benefit. It’s like the altruists only help each other when they’re in the group, and then they can do better against harsh conditions and disease, but the selfish agents, if they can’t keep next to the altruists, then they are all just individual agents: they never make a group. Because they can’t leach off of the altruists, they each have to fend for themselves. But, the altruists increase their resistance because they can form beneficial groups. They’re fitness is not just their strength, but it is also being capable of being part of a group."
Ashley’s notion of fitness originally relied upon the idea of an individual’s strength, or health. Until the disease model was introduced, she didn’t see a reason why individuals with lower baseline fitness would survive better than individuals who had a higher fitness. After she began thinking about disease and resistance, she envisioned the altruistic agents as sharing a natural resistance to the disease because of their benefit to each other. After she saw the effect of the Harshness condition on the success of the altruistic population, she reconceptualized her notion of fitness by incorporating the idea of group behavior into her notion of resistance. Ashley’s insight was that the ability to be part of a group was a fitness benefit that the selfish agents did not have.
An Insight into Group Selection
Richard, a freshman at Tufts University, is a mathematics major who has studied evolution in high-school biology. He came to the EACH project skeptical that altruistic agents could survive in head to head competition with selfish agents. After running the first model he remarked:
"If the altruists could get into groups, they might be able to survive."
However, he noted that because the original distribution was random, they could not possibly organize themselves into groups. Richard suggested that if the altruists started grouped together, then they might have a chance to fend off the selfish agents. To test this hypothesis, he divided the populations on the screen in half: he made the top half only altruistic agents, and the bottom half only selfish agents. He ran the model, and found that the selfish agents still won. After running the second model, Richard said:
"Look, they’re forming into groups, just like I said."
We agreed that forming into groups was the key to the altruists’ success, but Richard wanted to know why it happened in the second model and not in the first. He noticed that in the second model both populations had to drop significantly before the altruistic population gained enough "group-cohesion" to begin to dominate the screen. Then he said:
"Oh, the altruists need to have enough space so that their groups aren’t in competition with the selfish agents. I was right that they can’t win head to head; but, when there is harshness and disease, the altruists don’t have to fight with the selfish agents….The altruists help the selfish agents, but they don’t help the voids [his name for the unoccupied, or diseased, spots on the grid]. So, the altruists can benefit each other, and do better against the voids, than they can against the selfish….The voids keep attacking the selfish agents, and since [the selfish agents] can’t help each other, then the voids pull them off of the altruistic groups."
Richard’s idea was to think of the harsh conditions of the environment as an agent that didn’t get any benefit from the altruists. He saw that once these agents were in competition with both the altruistic and the selfish agents, they would stop the border areas of altruistic groups from being eroded. For Richard, they key was that once the populations became low enough, and the selfish agents were distanced from the altruistic agents, then the edges of the altruistic groups became areas of altruistic expansion, instead of selfish invasion. Richard’s insight was that the successful development of an evolutionary strategy, like group formation, was contingent upon the environment; and that such a strategy could, under sufficiently diverse conditions, turn the tide of a population’s evolutionary success.
A Model of Cooperative Behavior
A senior undergraduate at Tufts University, Geoff, came to the EACH project interested in whether a model of altruism could show the evolutionary success of a ‘real-world’ altruistic behavior. His initial intuitions had been aligned with the traditional view of individual trait selection, but once he explored the seed models, he began to think about what sorts of behaviors would actually result in evolutionary success for altruists. Since the first two models relied on variables for ‘cost’ and ‘benefit’, they did not offer any insight into what sort of altruistic behavior might affect the well-being of the group. Geoff wanted a more embodied model of how these complex interactions between individuals, groups, and the environment could be explained. So, together, we developed a third model: a cooperation (behavior) model.
The model consisted of two parts: cows and grass. The grass was designed to grow in such a way that above a certain height, it would grow back to its full height each turn, but below a certain height, it would grow back very slowly. The first type of cows, the "greedy", would eat the grass as far down as possible. The second type of cows, the "cooperative", would only eat the grass if it were above the fast-growth threshold.
All the cows had the same metabolism, and required a fixed amount of food to live. Each turn they lost a percentage of their energy, and if their energy ran out, they died. Eating grass restored a cow’s energy by a fixed amount. Finally, if a cow’s energy reached a certain threshold, it would reproduce. Thus, evolutionary advantage goes to cows who can get as much energy as possible. In this first version, the greedy cows were far more successful (See figure 3c, below).
In refining this first cooperation model into a second cooperation model, Geoff researched the evolutionary biology literature on population viscosity The only change to the model was to add a slider variable called ‘Viscosity’ to the control interface. The viscosity variable limited the range of movement of the cows, thus keeping the populations localized in their grazing habits. The change in the model behavior was dramatic.
Figure 3a below is the control interface for the Cooperation-Model 2. Figure 3b is the model at the start. The pink cows are the cooperating agents, and the blue ones are the greedy agents. Figure 3c is the Cooperation-Model 1 (viscosity of 0) after about forty cycles. Figure 3d is the Cooperation-Model 2 (run with viscosity of 8) after about four-hundred cycles.
Altruistic Behavior (Cooperation)Models
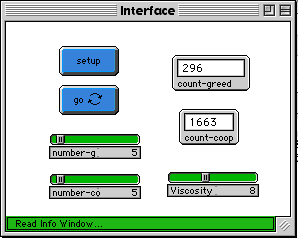 Fig. 3a |
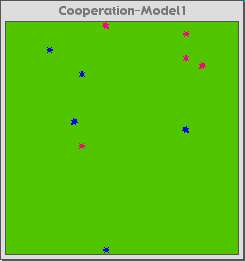 Fig. 3b |
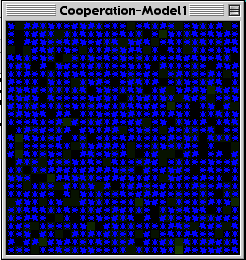 Fig. 3c |
 Fig. 3d |
Geoff quickly found that at a population viscosity value of about eight (which effectively limited the cows to one-eighth their normal travelling distance) the greedy population was kept to about a tenth of the cooperating population. And, at still higher viscosity values, the greedy population would kill itself off entirely. A still more interesting result was that the overall population of the cooperators, when they became the sole surviving population, was about four-times that of the greedy population when they became the sole surviving population. The cooperators evidently increased the carrying capacity of the environment four-fold.
Geoff concluded that as long as the greedy population was able to travel and use new resources, it would out-compete the cooperative population, driving the latter to extinction. However, when each populations’ resources were limited, and they had to stay within a localized region, the cooperative population fared far better than the greedy grass-eaters.
The seed models and activities that we developed as part of the EACH project, served the primary purpose of engaging students in exploring increasingly sophisticated models of the process of variation and selection. They came away from the altruism models with a new understanding of the relationship between environmental conditions and the effects of social considerations, such as group membership, on an individual’s evolutionary fitness. Through exploring the seed models, varying the parameters, and observing the consequences, they were able to build intuitive theories of what factors could affect evolutionary success
These insights led students to instantiate their new intuitions in working StarLogoT models. One student chose to model the success of cooperative vs. greedy behavior. His own investigation led him to an increased appreciation for the effects of population locality on the stability of cooperative strategies. Another student developed a model that uses an agent-based metaphor to model environmental coevolution. Still other students have begun to explore more complex models of the evolution of group behavior. Through a sequence of increasingly sophisticated and constructive experiences with these models, these students became increasingly sensitive to the difficulties of the "problem" of altruism and were able to meaningfully speculate about the implications of these models for understanding the relevance of altruism and cooperation at a human scale.
Axelrod, Robert M. (1984). The Evolution of Cooperation. New York : Basic Books.
Axelrod, Robert M. (1997). The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration. Princeton, NJ : Princeton University Press.
Bishop, B. A., & Anderson, C. W. (1990). Student conceptions of natural selection and its role in evolution. Journal of Research in Science Teaching, 27(5), 415-427.
Greene, E. D. (1990). The logic of university students' misunderstanding of natural selection. Journal of Research in Science Teaching, 27(9), 875-885.
Hamilton, W.D. (1964). The Genetic Theory of Social Behavior (I&II). Journal of Theoretical Biology. 7, 1-16, 17-32.
Jacobson, M. J., A. Sugimoto, et al. (1996). Evolution, hypermedia learning environments, and conceptual change: A preliminary report. International Conference on the Learning Sciences, 1996: Proceedings of the ICLS 96. D. C. Edelson and E. A. Domeshek. Charlottesville, VA, Association for the Advancement of Computing in Education: 151-158.
Mitteldorf, J. & Wilson, D.S. (in press). Population Viscosity and the Evolution of Altruism. Journal of Theoretical Biology.
Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
Papert, S. (1991). Situating Constructionism. In I. Harel & S. Papert (Eds.) Constructionism (pp. 1 - 12). Norwood, NJ. Ablex Publishing Corp.
Resnick, M. (1994). Turtles, Termites and Traffic Jams: Explorations in Massively Parallel Microworlds. Cambridge, MA, MIT Press.
Wilensky, U. (1995). Paradox, Programming and Learning Probability. Journal of Mathematical Behavior. Vol. 14, No. 2. p 231-280Wilensky, U. (1996). "Modeling Rugby: Kick First, Generalize Later?" International Journal of Computers for Mathematical Learning 1(1): 125-131.
Wilensky, U. (1997). StarLogoT. Medford, MA, Center for Connected Learning and Computer Based Modeling, Tufts University.
Wilensky, U. (1997). What is Normal Anyway? Therapy for Epistemological Anxiety. Educational Studies in Mathematics. Volume 33, No. 2. pp. 171-202
Wilensky, U. (1998). Connected Models. Medford, MA, Center for Connected Learning and Computer Based Modeling, Tufts University.
Wilensky, U. & Resnick, M. (1999). Thinking in Levels: A Dynamic Systems Perspective to Making Sense of the World. Journal of Science Education and Technology. Vol. 8 No. 1.
Wilensky, U. & Reisman, K. (1999). ConnectedScience: Learning Biology through Constructing and Testing Computational Theories--An Embodied Modeling Approach. InterJournal of Complex Systems, M. 234, pp. 1 — 12.
Williams, George C. (1992). Natural selection : domains, levels, and challenges. New York : Oxford University Press.
Wilson, D. S. & Sober, E. (1998). Unto Others: The Evolution and Psychology of Unselfish Behavior. Cambridge, Mass. : Harvard University Press.
Acknowledgements
The preparation of this paper was supported by the National Science Foundation (Grants RED-9552950, REC-9632612). The ideas expressed here do not necessarily reflect the positions of the supporting agency.