
|

|

|
Assessing Learning as Emergent Phenomena
Moving Constructivist Statistics Beyond the Bell-Curve
To appear in Kelly, A.E. & Lesh, R. (Eds.) Research in Mathematics and Science Education. Englewood, NJ: Erlbaum.
| Dr. Walter M. Stroup | Dr. Uriel Wilensky |
| Department of Curriculum and Instruction | Center for Connected Learning |
| The University of Texas at Austin | Annenberg Hall 311 |
| Austin, TX 78712-1294 | Northwestern University |
| 2120 Campus Drive | |
| Evanston, IL 60208 |

|

|

|
Taking the Measure of Measuring
Reconsidering the Beginnings and Ends of Assessment
Assessment, in the context of learning, serves two purposes. First, assessment renders or typifies the nature of understanding for an individual or a group. Second, assessment addresses expectations about learners ’ possible future performance. As a practical matter it is reasonable for educators and researchers to ask: Has an intervention succeeded?; Can one intervention inform another?; Are there expectations we might reasonably have about what learners can now do in other settings?
More formally, assessment is an attempt to establish equivalence classes that can typify and form the basis for reasoning about groups of learners and individuals within those groups1. This chapter takes up the issue o f formal assessment and the rendering of knowing on a scale larger than one (or even a few) learner. It is addressed principally to our colleagues within the constructivist research community, but it may be of interest to other researchers or educators w ho see learning as the emergence or the development of cognitive structures2
* in a rich web of intellectual and social connections.In this chapter, our principal goal is to critique the standard statistical model of assessment used by educational researchers both to depict the state of knowledge of a group of learners and to track the evolution over time of the group’s kn owledge in order to evaluate the success of an educational intervention (activity). We will show that the standard assessment models based on the use of standard parametric statistics is both fundamentally flawed and essentially incompatible with constructivist theory. A subsidiary goal, which will serve as an introduction to our critique of standard statistical models of group assessment, is to critique the "technology" and methodologies of assessment of individual stude nts over time, arguing that the methods of assessment employed are impoverished and that, in an attempt to summarize performances quickly, they throw out qualities of performance that are essential to getting adequate accounts of an individual’s und erstandings. We continue by outlining the qualities that must be characteristic of an adequate assessment methodology and sketch a nonstandard assessment methodology that addresses many of the flaws of traditional methods. Some limitations of the new met hods are addressed. We conclude by suggesting ways in which new computational technologies can be employed to create richer assessment methodologies that both correspond more closely with constructivist theory and provide a much more detailed and illumina ting account of learners’ development.
What’ s in a Number? How Does Standard Numerical Assessment Depict Learning?
The principal goal of critiquing the methodology of group assessment (and the assessment of educational interventions) exists against the backdrop of problematic, school-based, assessment practice. For most school districts, the end of a school ye ar is marked by each student receiving a collection of numerical (or letter) grades, usually arrived at by averaging performances over the year. Averages are also computed for various groupings of learners: sections of a given course, schools in a syste m, and even districts as a whole. All of this is so standard as to be beyond the reach of criticism -- as unavoidable as the changing of the seasons. The need to summarize students’ performance is seen as natural as the expectation that averages (a nd standard parametric procedures) would be the methods used to create these summaries. What we hope to do is separate the need to summarize or typify learning from the particular methodologies employed currently. We seek to distinguish the assessmen t of learning from the simple averaging of numerical quantities. In this section, we point out that such numerical averaging methods exist as a point or a small region within a vast space of possible assessment methodologies. Moreover, standar d averaging methods are particularly impoverished ways of typifying learning and knowing, ways that give educators and researchers very little of the insights they need in order to practice their crafts better. Additionally, the computing of these average s carries with it a deeply suspect model of learning and knowing that may undermine efforts at meaningful reform.
Among the observations we make is that a computed average -- for example, B+ or 85 -- is, by nature, degenerate. We use "degenerate" in the mathematical sense -- that it represents a huge reduction in the dimension and richness of learn er performance. A final course grade reduces hundreds of hours of performances, activities, beliefs, thoughts, emotions, and peer interactions to a single value. This richness is lost irretrievably to the larger educational enterprise. Consequently, the re is a profound reduction in what can be said about learner understanding. This, in turn, provides inadequate feedback for educators to use in developing classroom activities and little information for researchers to use in reconstructing learner thoug ht. Both classroom activity and research into understanding are compromised by the degeneracy of the averaging methodology.
A subtle and widely held "misconception" about averaging is that it is the most objective and theoretically neutral technology for reporting summaries of multiple performances. Because objectivity and neutrality are seen as desirable i n assessment, averaging is seen as desirable. In principle, there are an infinite number of ways of combining values, all comparably objective, none theoretically neutral. Thus, averaging is not a privileged methodology. A basic example will illustrate the point that even a report of something as simple as a calculated average requires a selection of methods and a theory or model to suggest what the number signifies and how it could come to represent such a thing.
In what sense can we speak of an average square? Suppose we have two squares, square A with side 2 and square B with side 10. What is the average of these two squares? In computing this average, a question is provoked immediately over whether we are referring to the sides of the squares or the areas. In the former case, we average the length of the sides and find that the average square is of side (2 + 10 ) / 2 = 6 units of length. In the other case, we average the areas of the squares, whic h yields an average area of (100 + 4) / 2 = 52 square units. So, on the one hand, the average of the two squares is a square of side 6. On the other hand, the average square is of area 52. Even if we corrected for the dimensionality by taking the squa re root, we end up with an average square with side of length greater than 7. Which is the real average square: the 6 or the 7? When averaging, one needs to be explicit about what one is paying attention to.
A more significant observation about this example is that neither average says anything at all about squareness as such (if, indeed, there is any such thing as squareness as such). So average squareness is underdefined or missed al together, even if agreement is reached about which numbers are used to compute the average (sides or areas). All sorts of averages can be created and defined operationally as measuring a given property (like the average square). Our argument is that even when careful attention is paid to such operational definitions, it still may be the case that the model implied by averaging of this sort does not fit with, or in any way render, the intended object of attention. In the example given abo ve, squareness itself is missed. Instead, one ends up with various averagings of selected features of certain geometric figures and not an account of the presence of squareness that is presumed to be at the center of the investigation.
The situation is similar, we argue, with assessing learner understandings. Various averages can be computed. Often, ambiguity of the sort alluded to in the square example is present: Are we talking about analogs to areas or to sides (or a mixtur e of these and still other properties)? More fundamental, however, is the question of whether a statistic based on averaging is a statistic that can say anything meaningful about understandings as such. When using computed averages in assessing understa ndings, we want to ask: Are we merely measuring somewhat arbitrary features of human activity and missing the mark altogether in our attempt to give an account of understanding as a developing, structured, and structuring whole? We believe that cognitiv e statistics -- as a rendering of equivalence classes among learners -- are indeed possible. But, in order for the intended objects of our attention -- understandings -- to be rendered, it is not expected that these statistics will be based on a notion o f average understanding or that they will be well served by the use of various kinds of related parametric procedures.
In educational assessment, we believe that a part of the reason that averages have been selected from among the vast range of possible renderings is because they are comparatively easy to compute. That is, given the technologies of pencil and paper , adding machines, etc, the average is amongst the simplest of computations. "Averagers" customarily ignore the role of computing technologies in forming and biasing the selection of the standard average. This lack of awareness of dependency on the ease of computation has numerous consequences. Among them is that even with the advent of new, computer-based technologies, we have failed to address the new possibilities inherent in the more powerful medium and, instead, have carried over the old m ethodology to the new medium. In our concluding section, we suggest assessment renderings that make better use of powerful new technologies.
Given that any reporting of outcomes results from theory and norm-based selection of procedure, we note that, under current practice, the possibility of having this valuation and consequent analyses informed by, and reflective of, local norms and e mphases is not considered. This means that local educators are tacitly deferring to a centralized testing authority to decide important issues of valuation. This deference may relate to the presumption of greater objectivity associated with averaging, d iscussed above. New computing tools would allow the analyses to be powerfully contextualized and tailored to better address local needs and norms.
In the next section, we take up the major argument of this chapter -- the critique of standard statistical methodology for group assessment. In doing so, we are aware that we are taking a strong stance regarding the interaction of methods and model s of learning. Although positivism, as a philosophy proper and as a theory of scientific method in particular, has been widely rejected, some positivistic assumptions about methodology still linger in the education research community. Most notable is the assumption that methods can be cleanly separated from models or that given methods can be "theory neutral" (see, e.g., Kuhn, 1957, 1962/1970). The argument that follows assumes that methods and models are inextricably linked and mutually info rming.
Critique of Standard Group Assessment Methodology: Rejecting the Efficacy of Methods without Models
Now we come to our principal argument -- that standard statistical methodology implies a model of learning that is largely incompatible with fundamental elements of constructivist theories of learning centered on the development of cognitive struc ture. If, in fact, the emergence of whole cognitive structures does typify the developmental sequence, then we would expect individuals’ progress to show a more discrete quality to it and not be well modeled through a continuous distribution with a n incremental time-evolution. The understandings of groups of learners would emerge as vectors in an evolving, structural, n-space. The time-evolution of the locations of populations associated with these vectors would not be monotonically increm ental but, rather, would have a significant stochastic aspect. The image is less like a planet precessing and more like the discrete restructurings associated with various quantum phenomena. In this section, we expand upon and develop these ideas further . Subsequently, we present the outlines of a nonstandard statistical methodology more compatible with fundamental elements of constructivist learning theory.
The reasonable rejection (avoidance) by some constructivists of the standard model and its associated methodology has resulted in the creation of what we see as a problematic response -- a methodology that we call "radical individualism". In the work associated with this methodology, it is sometimes unclear in what sense the reported work is about more than one (or a few) person(s). Such work risks being too individual in a way that Piaget rejected explicitly as a characterization of h is constructivism (Bringuier, 1980). In this chapter, we outline an alternative to either standard parametric methodologies or the methodologies of radical individualism.
Admittedly, the topic of formal assessment is an awkward one among constructivists and one that most are hesitant to engage. For many, there is the danger of becoming too consumed by methodological issues that will take them far afield from the ki nds of learner-centered research activities that interest them most. Piaget expressed something like this idea3 and Duckworth (1987) has expressed similar sentiment4. Papert (personal communicat ion, April 1993) has justified his lack of interest in statistical assessment methodology by saying that if you need statistics to show an educational improvement then the improvement was not significant enough to warrant our attention. Problems, howeve r, are created by this inattention. On the one hand, this seeming incoherence in the methodologies of various cognitive researchers can hamper efforts to have one set of results inform another and, on the other hand, it can give critics a too faci le reason for not engaging the substance of the research findings. Most significant to us, however, is the possibility that some researchers’ allowance that standard parametric methods are acceptable could, in the end, advance indirectly a model of learning largely incompatible with constructivism’s attention to the emergence and development of learners' cognitive structures.
Skepticism has been expressed about the utility of statistical assessment in the educational reform community. This skepticism has had a significant impact on discussions of practice and attempts to create new educational standards. Many reform documents and articles call for nonstatistical assessment techniques including portfolio assessment (Cai, 1996a, 1996b, Lambdin, 1996, Mathematical Sciences Education Board, 1993a, 1993b, National Council of Teachers of Mathematics, 1989, 1992a, 1992b, 1 995, Vermont Department of Education, 1991). While constructivist educators have made some significant inroads on assessing individual learners, constructivist researchers have had much less to say on largescale assessments (classrooms, schools, districts , states, countries). Moreover, as a practical concern, the aggregate of portfolios overwhelms the capacity of the classroom educator to process the input in a way that would inform ongoing practice. Additionally, a number of critiques of statistical a ssessment methodology in relation to educational research have emerged. Some have noted that "classical" educational research, with its use of standard statistical methodologies, emphasizes product over process (Schoenfeld, 1987). Others have noted that standard statistical methodologies can do little to inform the interventions needed for children with special needs (Meltzer, 1994). There have been calls for a temporary suspension of statistical assessment until methods integrated more close ly with analyses of thinking processes are found (Kilpatrick, 1978). Our sense is that significant work needs to be done related to analyzing the theoretical aspects of the relationship between standard statistical methodologies and constructivism and to providing constructivist alternatives for large-scale assessment.
Ours, then, is a very pragmatic concern. We see the edifice of school-based, behaviorist practice that resists putting the ideas of learners at the center of education discourse as standing on a foundation of standard parametric methods. Therefor e, we believe it is worth considering how an embrace of the latter may do much to reinforce the former. One purpose of this chapter is to encourage developmentalists and constructivists of the various hues to take up again the issue of how we render lear ning formally on a scale larger than one (or even a few in a teaching experiment). We intend this chapter to begin this process of reconsideration even as it seeks to give specific guidance to researchers and educators "in the field" looking fo r ways of analyzing the activities of learners.
Heuristic Realism and the Gaussian Distribution
The Fit between the Use of Standard Parametric Methods and Behaviorist Learning Theory
Although, in discussing learning research, many cognitivists -- including constructivists (e.g., Piaget, as quoted by Bringuier, 1980) and Gestaltists (e.g., Köhler, 1959) -- have allowed that standard statistical methods could be used aft er the more important work of discovery has been done, it is argued here that the use of standard norm-based statistics (classical parametric methods, as discussed by Siegel [1956] and Stevens [1946, 1951]) implies a model of learning that fits better wit h the central features of behaviorism than with structure-based cognitivism. Deeper reasons why Piaget, in particular, may have continued to allow for the use of parametric methods may have more to do with his philosophical stances regarding the foundati ons of chance-based reasoning and the relations between science and religion than as an assertion about the adequacy or appropriateness of these methods in the realm of learning research (Stroup, 1994, 1996). These reasons are not the focus of this chapt er because they take us quite far away from an analysis of standard parametric methods as vehicles of learning research and assessment.
Later herein, we will give an example of where Piaget, despite his seeming allowance for the use of standard statistics, did advance nonetheless a kind of nonstandard statistic in reporting the results of some work with learners. We believe that t his nonstandard statistic may hint at the possibility of advancing a more thoroughgoing effort to develop nonstandard statistics that fit better with the central tenets of structure-emergent, learning theory. Thus, while the ambivalence regarding standar d statistics is long-standing within cognitivism, the possibility of resolving the internal tension in a way that allows for the creation of formal equivalence classes (necessary for the creation of any kind of statistic) while remaining true to cognitive theory is highlighted. To move toward this resolution, it is important to make clear the ways in which standard statistics seem to fit better with behaviorism as a theory of learning. The behaviorism considered is the classical stance represented in th e writings of B. F. Skinner, the chief architect of this now traditional model of learning.
The precursors to parametric statistics certainly predate their application to what Skinner called a "science of behavior." The first efforts to develop a formal manner for discussing fluctuations or errors in scientific measurement came in the field of astronomy in the latter half of the eighteenth century. Early astronomers needed a system for talking about the variations occurring in their measurements of specific celestial objects (Heidelberger, 1987). A notion of what eventually b ecame "standard deviation" was developed. If the standard deviation for a particular set of measurements was relatively large, then other scientists would know that a good deal of fluctuation had occurred in the measured results. A relatively low standard deviation meant that the results were relatively consistent.
In the nineteenth century, Karl Friedrich Gauss helped to formalize the discussion of standard deviation (Swijtink, 1987) and give it the numerical interpretation that it has today (i.e., allowing that the results are consistent with the central li mit theorem, within one standard deviation of the mean, one can expect to find nearly 68% of the trials in a normal distribution). In the realm of celestial observations, the assumption that there is some one thing being examined (assuming a certain leve l of competence) and that this same one thing continues to exist while observations are made seems entirely reasonable5
Social theory based on the use of statistics inverts this argument. Rather than moving from a real object being observed to the use of a certain kind of statistics, the argument in social science (including traditional forms of behaviorist analysi s) moves from the use of a certain kind of statistics to the assumption that there is something there that is being measured. A kind of operationally-defined or heuristic realism takes hold.
When a concept is defined in terms of the operations, manipulations, and measurements that are made in referring to it we have an operational definition. Intelligence might be defined as the score obtained on a particular test, a character trai t like generosity might be defined as the proportion of one’s income that one gives away (Cowles, 1989, p. 41; emphasis in the original).
As noted in the quotation, intelligence is defined operationally as that which the score on an intelligence quotient (IQ) test measures -- what the statistics point to. Even characteristics like "generosity" can be made real by the similar use of an operational definition.
The positivist commitments of operationalism require that "meaning is equated with verifiability" and that constructs that are not accessible instrumentally to observation "are meaningless" (Cowles, 1989, p. 41). Of course, thi s approach is "closely akin to the doctrine of behaviorism" (Cowles, 1989, p. 41). The language of thought, meaning, or intent (to say nothing of aesthetics) is eschewed in scientific discourse and is replaced by the object ive measurement of behavior.
Although positivism, as such, is decidedly antirealist, a kind of implicit notion of deterministic mechanism still informs behaviorist discourse.
It is a working assumption which must be adopted at the very start. We cannot apply the methods of science to a subject matter which is assumed to move about capriciously. Science not only describes, it predicts. It deals not only with the past but with the future .... If we are to use the methods of science in the field of human affairs, we must assume that behavior is lawful and determined. (Skinner quoted in Cowles, 1989, p. 22; emphasis added).
The "field of human affairs", including education, "must" be "lawful and determined" in much the same way that the motions of planets are objectively determined. The "methods of science" require that this be so. Thus, in using these methods, it is "assumed" that the behavior under consideration is as lawful and determined as it is seen to be (at least under classical models) in other realms of science. The flow of the argument is not from the object (e.g., a planet) to a method. Instead, the move is from the application of certain "methods of science" to the assumption that there must be something "lawful and determined" there to be measured. In this particular way, behaviorism labors under the assumption of a kind of operational or heuristic realism.
Extending the sense in which behaviors are analogues of physical objects, such as planets, a new class of object is introduced -- a behavioral object. Some objects of behavior are immovable (like the "fixed" stars). Still others can be advanced (like planets traveling in their orbits). Intelligence as a behavioral object, usually is seen to be fixed. It is the first mover of knowing-type behaviors. A properly calibrated test simply measures where this unmoved mover is l ocated. In this way intelligence is understood to be largely above interventions of any kind (except, of course, certain types of physical trauma)6.
Examples of intellectual objects that can be seen to move include performance or achievement in some field of knowledge7. Achievement in doing sums or in doing physics can be measured using a testing instrument. Usual ly by some form of intervention (the behavioral equivalent of a physical push or shove), the level of achievement can be improved. This improvement can be measured in individuals and in groups. By using properly calibrated instruments, the motion or mov ement of the behavioral object can be assessed experimentally.
For a group of learners working on a standardized examination in physics (e.g., like those produced by the Educational Testing Service), an improvement in scores represents a "real" improvement in achievement.
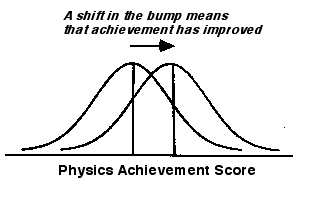
Figure 1. The significance of a change in achievement scores.
If the bump of collective performance moves to the right, as illustrated in Figure 1, then the intervention (e.g. increased classtime, use of a particular text, or animated lectures) is labeled effective. Performance, understanding, or ability in almo st any area can be defined operationally in such a manner, and the effectiveness of an intervention can be established object-ively. School curricula and pedagogy rise and fall according to their ability to shift the bump of (what is assumed to be ) a normalized distribution.
Some Characteristics of Traditional Statistical Models
In light of the radical epistemic shifts that have taken place in physics and astronomy since they became modern (including specifically the use of nonstandard statistical distributions), it might seem reasonable to ask whether methods borrowed from the natural sciences during their mechanistic (classical) period might need to be updated. Certainly, there has to be some irony in the fact that one of the few major realms of formal academic discourse where a kind of mechanistic realism persists is in the quantitative methods divisions of the various social science departments (including education). These observations notwithstanding, it remains beyond the scope of this Chapter to review fully, much less engage in detail, the extensive literatur e concerning the validity of using traditional statistical methods8. For the purposes of analysis, a few features of the traditional model need to be highlighted:
The distribution of intelligence, achievement, or understanding in a group looks like a bump (a Gaussian distribution) in the traditional schema (see Figure 2).
Figure 2. The Guassian Distribution.
At least in principle, the distribution of learnable performance for a group of individuals (the bump shown in Figure 2) can move quasi-continuously (there may be small jumps due to the discrete nature of the assessment items; nonetheless, the mathematics, in a sense, requires that the distribution approach -- as a limit -- a continuous curve and be able to move up or down relatively smoothly). Complex behavior is analyzed into "small steps" and behavior is shaped "through a pro gram of progressive approximation" (Skinner, 1978, p. 135). Based on the results gleaned from the "laboratory", learning "[m]aterial is so designed that correct responses are highly probable" (Skinner, 1978, p. 135). Ability i s advanced incrementally as correct responses to individual contingencies become more probable (Skinner, 1978).
Illustrating Skinner’s (1968) strong commitment to incrementalism is his own "conservative estimate" of "the total number of contingencies which may be arranged during ... the first four years" of schooling (Skinner, 1968, p. 17). His estimate for these years alone is "[p]erhaps 50,000" (Skinner, 1968, p. 17). For a scale with such fine-grained increments, global advancement would appear near-continuous9.
• The bump is assumed to stand for, or represent, a single thing (e.g., general intelligence for fixed bumps, or understanding of mathematics for movable bumps) or a single cluster of abilities (e.g., scholastic aptitude). For movable achievemen t, this identity is preserved even as the bump moves up or down the range of possible values. The sense is that there is some one thing, like a planet, being moved and, when the bump moves, the something -- for example, achievement -- is now located in a new place.
• There is no need to engage, or even to acknowledge, the existence of learners’ ideas, models, or modes of reasoning. Not only are investigations of such structures a distraction from empirical investigations of behavior, but also they are doomed in principle to be misleading. Skinner argues specifically that "introspective knowledge is limited by anatomy" (1978, p. 73). For a person, self-observation and the ability to investigate "why he behaves as he does" are seen to have "arose very late in the evolution of the species" (Skinner, 1978, p. 73). When "why" questions are asked about ourselves (or, even more difficult, when "why" questions are asked about others), "the only nervous systems available" are those that have "evolved for entirely different reasons" (Skinner, 1978, p. 73). That is, the nervous systems that had "proved useful in the internal economy of the organism, in the coordination of movement, an d in operating upon the environment" are being pushed well beyond their specific capacities in being asked about ideas or internal models (Skinner, 1978, p. 73). According to Skinner, there is "no reason why they [the nervous systems] should be suitable in supplying information about those very extensive systems that mediate behavior" (Skinner, 1978, p. 73). The nervous systems simply are not designed to do this. Fundamentally introspection is suspect;
...introspection cannot be very relevant or comprehensive because the human organism does not have nerves going to the right places (Skinner, 1978, pp. 73-74).
In the end, Skinner’s very personal theory or model of the evolution, purposes, and design of the nervous systems (briefly outlined above) preemptively precludes the possibility of engaging the thoughts or reasoning of learners10. The whole of semiotic activity as such is suspect as the stuff of formal ("scientific") investigation. All there is to teaching within his behaviorist framework is the programatic manipulation of the contingencies o f reinforcement. Learners’ ideas, symbolizations or structures of thought are absolutely irrelevant to Skinner’s notion of a science of behavior.
Taken together, these assumptions are seen to underlie or reinforce the use of statistics in ways closely identified with the larger behaviorist program. Having outlined the bases for the external identification of standard statistics with behavio rist learning theory, we now take up some issues related to the internal inconsistency of standard statistical methods as they are applied to learning.
Internal Deficiencies of Standard Parametric Methods
Setting aside, for a moment, the external identification of standard parametric methods with largely discredited, behaviorist learning theory, significant internal fault lines can be found in the systematic application of standard paramentric methods to assessing learning. In education, standard parametric methods have shown themselves to be well suited to sorting and ranking learners within a consistent interpretive scheme. Beyond simply sorting learners, however, the methods fail to say much that is meaningful or useful about learning itself. The processes, beliefs, content and activities of learning are not illuminated. By examining closely some of the internal theoretical and practical deficiencies of the application of s tandard parametric methods, we hope to raise serious questions about the integrity of seeking to apply these methods in education contexts.
Classical statistical theory as applied to social science, has a number of fundamental assumptions. Among the five that Siegel (1956, p. 19) lists is "[t]he observations must be drawn from normally distributed populations." In actual practice, ho wever, the appearance of normal distributions, even in large-scale achievement and psychometric measures, is extraordinarily rare. An article by Micceri (1989) with the provocative title "The Unicorn, the Normal Curve, and Other Improbable Creatures " made this point convincingly. Micceri undertook a review of 440 large-sample achievement and psychometric measures. The striking result of this review was that less than 7% of these data sets exhibited the symmetry and tail weights of the normal (Gaussian) distribution. In addition to mixed-normal distributions (distinct peaks), other important kinds of distributions occurred regularly. A more recent survey (Sawilowsky, 1990) of these issues highlights a similar sense in which typical di stributions associated with learning research and assessment almost never satisfy the fundamental assumptions required for the use of parametric tests such as the t and F tests for analyzing sets of experimental data.
In part as a way around these very significant failures of the standard parametric model to work as a statistic in the learning sciences, a rather defensive response has emerged from parametric researchers. The goal seems to be to preserve the cal culating machinery of various ANOVA techniques even when the fundamental assumptions that structure the use of the techniques fail. Strategically, an effort is being made to avoid linking specific forms of calculation with either theories of behavior or classical theories of parametric method (e.g., Stevens, 1946; Siegel 1956). The break with the fundamental assumptions of classical parametric method is startling. Even when fundamental assumptions (like normality, etc.) that structured the use of thes e algorithms are violated, these researchers still want to continue to use the calculating machinery.
The argument of these researchers is that the calculating techniques themselves become a model and are no longer to be considered methods associated with other models. In justification, it is no longer a question of whether the "normal theor y ANOVA assumptions" (as discussed by Siegel [1956, p. 19], for example] are "met", but "whether the plausible violations of the assumptions have serious consequences on the validity of probability statements based on the standard ass umptions" (Glass, 1972). For these researchers, the probabilities associated with ANOVA tests being run on various nonnormal distributions (see Siegel, 1956) were close to the probabilistic results from Monte Carlo simulations. Because the numbers worked out to be very similar, there was little danger in continuing to use ANOVA statistics even when the conditions that structured the use of these statistics are absent. Glass (1972) summarizes the situation somewhat cavalierly this way: &qu ot;The assumptions of most mathematical models are always false to a greater or lesser extent." The statistical bottom line was (and is) this: ANOVA tests work and there is no need to become engaged in trying to justify their continued use in any o ther way. Formally, the ANOVA tests themselves are to be considered a kind of "model". Researchers can act as if this model is true just so long as reasonable probabilities are produced.
Although the point needs to be developed further in future work, those familiar with the history of science may recognize some striking parallels with other important moments of paradigm shift. By the time of the Copernican revolution, the mathema tical machinery used to calculate the position of various planets and the stars assuming a geocentric model was quite advanced. There was little (if anything) in the formalism that could have compelled the major revision that was the Copernican re volution. The mathematical model was quite powerful11. What became increasingly untenable was the effort to see in the world the structures that would allow the formalism to make sense.
Similarly, the criticism of traditional statistical models advanced in this chapter is not particularly informed by failures of the mathematics to "save the phenomena." Instead, it is informed by the failure of the mathematics of the par ametric model to make sense of itself and to make sense of learning. At this point in our intellectual history, it seems as if the methods of various tests have been divorced from the assumptions that grounded the use of these tests. Moreover, th e whole of the effort to do research in statistical methods has attempted to divorce itself from discourse about the nature and processes of cognitive activity. Once again, there is an attempt to separate neatly the methods from the content and meaning o f the work done with those methods.
One of our aims in this section is to remind ourselves that, historically, there were links between models of learning and methods. Additionally, we hope to advance the idea that coherent alternatives to the current pastiche of methods, ma thematics, and theories of education might are possible. This sense of alternatives emerges, we believe, in underdeveloped strands from the constructivist literature. We begin with an example from Piaget.
An Early Example of a Constructivist Statistic
Piaget's book, The Child's Conception of Movement and Speed (1946/1970a), reports his investigations of children's ideas about changes in position and speed. Methodologically, the findings are largely the product of clini cal interviews. At one point, however, Piaget summarizes his results in a way that is distinctly quantitative. He uses a simple quantification scheme -- quoted below -- to draw together important strands in his work. This quantification conveys insight s about children’s ideas of motion, aspects of his larger developmental project (with its specific references to age), and an overview of the collective performance of "some sixty subjects of 5 to 10 years of age" (Piaget, 1946/1970, p. 227 ). This rendering allows Piaget to speak "both" to "their agreement with previous results" and to "the individual light thrown on the problem of speed" (1946/1970, p. 227). Both general (i.e., developmental) and quite narro w (motion-specific) concerns are thereby addressed. While a weakness of his account might be that it does not seem to allow for the full bidirectional interaction of collective results and individual reports which the nonstandard statistical methodology developed in this chapter does allow, it is still the case that what Piaget does report instantiates an effort on his part to articulate collective results in ways consistent with his larger developmental claims.
Piaget advances a non-standard ‘model’ centered on learning issues related to the development of motion and rate structures (1946/1970, p. 227). This brief quantitative report we view as significant because it suggests new methodologica l and theoretical possibilities for the development of nonstandard statistics centered on the emergence of cognitive structure. It is precisely to this possibility that we want to draw attention and we would like to see it extended by other cognitive res earchers.
Piaget (1946/1970, p. 227) summarizes some of his motion-related results from "some sixty" learners in the following way:
From the point of view of time, first of all, confirmation is found of what has already been seen in other work: simultaneousness of finishing points (or even starting points) is acquired at the age of 5 years by only 25% of the subjects; at 6 years b y 50% and at 7 years by 75%. As for the equality of synchronous durations, this is on average slightly delayed: 33% at 5 years, 25% at 6 years, 70% at 7 years, and 75% only at 8 years (1946/1970, p. 227).
The report is nonstandard in that no (even implicit) reference to a normal distribution is advanced nor are related reports of uncertainty (plus or minus) made. Instead, specific assertions about shifts in understanding are reported as a function of a ge. In the context of the quotation, "simultaneousness refers to learners identifying that objects moving together for the same amount of time but for different displacements finish together (as opposed to a single object that went farther for more time). "Synchronous duration" concerns learners seeing the objects as having moved for the same amount of time ("duration", as opposed to stopping at the same instant, as with "simultaneousness").
If Piaget’s findings are plotted on three-dimensional axes, the respective graphs for the development (time-evolution) of simultaneousness and synchronous duration that result are shown on Figures 3 and 4.

Figure 3. Time evolution of performance for simultaneousness.
As Piaget reports, synchronous duration is "slightly delayed,"so the shift in performance comes later ("75%...at 8 years").
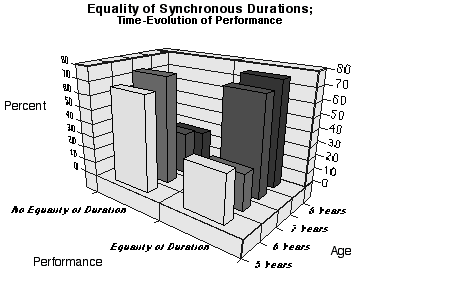
Figure 4. Time-evolution of equality of synchronous durations.
"Performance" is seen as the exhibition ("acquisition") or nonexhibition of a way of thinking about a task. Piaget’s way of analyzing the behavior of the learners is organized in terms of shifts in understanding or ways of thinking -- simultaneousness or equality of duration -- and not in terms of a continuity in the identity of the specific collections of students either exhibiting or not exhibiting a kind of behavior or performance (this identity is required un der the heuristic realism associated with the standard statistical model). It is expected that the individual students associated with particular kinds of performance would change over time.
Students restructure their thinking and their performances change. While the results that Piaget reports are not from a longitudinal study, it is clear that he does expect that his finding would typify the development of any particular grou p if it were followed over time. This means the narrative is not merely a description of fourteen separate groups of students (represented by each bar of the graphs in Figures 3 and 4). Rather, an overarching account of development is being advanced.
Attention to shifts in learners’ understanding is the salient feature of this framework. This contrasts with the standard model based on the incremental acquisition of ability, judged in relation to changes in a particular colle ction or sample. What are conserved in Piaget’s model are the modes of thinking, not the populations associated with these modes. The traditional notion of sample is largely abandoned. Piaget even goes so far as to allow that the reports at variou s ages can be of completely distinct groups of learners. He is that confident in his account, which is centered on shifts in understanding.
Not only is the organization of the analysis of performance distinctive, but so, too, is his treatment of children not exhibiting simultaneousness or equality of duration. The ways in which learners do not exhibit simultaneousness or equality of d uration are as important to Piaget’s investigations as the characterization of the thinking of the students who have operationalized these conceptions. Nonsimultaneity and inequality of durations are still seen as ways of thinking and acting. Indeed, at least as much time is spent analyzing and making sense of the properties of the students not exhibiting simultaneousness or equality of duration as is spent articulating what it means for students to have acquired these structures of thought.
This attention to earlier thought and to changes in thought reflects general theoretical commitments that Piaget advanced throughout the whole of his life’s work. These commitments are a starting place for the possible nonstandard quantificat ion system suggested in this chapter. Themes in Piaget’s universalistic developmental project can be drawn on to begin examining of the nonstandard quantification scheme presented herein. However, the particular commitments of the methods that we o utline do not require the structures to be universal in the way that Piaget pushed for. Instead of focusing only on universally emergent structures that may characterize the development of intelligence itself, the methods we propose would allow for atten tion to nonuniversal structures that can characterize understanding within particular realms of human accomplishment and creativity (Stroup, 1994, 1996). The methods we propose take seriously the role the forms of embodiment and types of symbolization we use have in actually shaping emergence of non-universal structures (Wilensky, 1993; 1997). The representations we use are shape what it is that we know. The development of these non-universal structures are recognized by at least some neo-Piagetians as what "most of the energy of most of the people in most of the world" is spent trying to "achieve" (Feldman, 1980 p. xiii-xiv; see also Gardner, 1989, p. 114).
The nonstandard quantification scheme, introduced below, is presented as an alternative to standard analyses based on the use of normalized distributions. In presenting this non-standard quantification scheme, an explicit connection is made betwee n particular theories of learning and certain methods of quantification. The positivistic presumption that there is a clean line separating method from message is rejected. The idea advanced is that while Piaget does allow for the use of standard statis tics at some points, on the whole, a non-standard statistic (of roughly the sort that he invokes above) needs to be developed to analyze the changes in thinking of learners. This nonstandard quantification system should fit better with the morphology of the cognitivist theories of learning that are centered largely on the emergence of structure.
Toward A Nonuniversal Constructivist Statistic
Outlines of an Emergent Framework
The characteristics of a nonuniversal constructivist framework for the analysis of collective performance are outlined below. This nonstandard quantitative framework will fit with and extend the cognitivist model h inted at in Piaget's example. The idea is to cross the positivistic divide of meaning and method. The quantitative features of the constructivist statistics discussed below have sufficient experimental content so that they are applicable to the interpre tation of the data sets that our fellow researchers may encounter. This framework is emergent because, unlike the behaviorist stance outlined above where the emphasis is on uncovering and measuring already existent objects of performance, it seeks to inf orm us about understandings that come into being in relation to activity. These understandings are constructed in ways that can not be reduced to the individual "responses" or "contingencies" of performance, or to the linear summation (accumulation) of these "responses" or "contingencies" (see the earlier discussion of Skinner).
1. The distribution of performance on a complex task will not belong properly under one bump. In general, the frequency distributions will be bi- or even multimodal (see Figure 5).
Although, conceivably, various parametric tests might show that there are indeed two (or more) distinct modes present, no presumption of normal distribution in any of the modes is advanced. Among other significant shortcomings, the time-evolution discussed in 6. below would be difficult to account for if one expects the identity of the populations associated with each mode to be preserved. The assertion made in this work is merely that distinct modes will appear in the data.
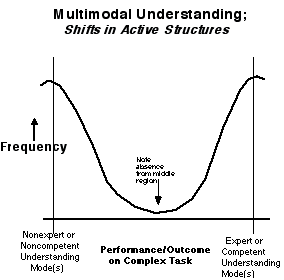
Figure 5. Shifts between modes of understanding.
In this framework, "expert" is viewed as a convenient shorthand for a well-connected (see Wilensky, 1991, 1993, 1997) form of understanding as it exists among other forms of understanding. It does not refer to a fixed or final intellectu al resting spot. Moreover, what constitutes "expert" or what is seen to constitute "expert" in this framework has significant sociocultural dimensions in ways that might not be compatible with the ways in which "expert&quo t; is used traditionally in "expert systems" or novice-expert study parlance. Under this framework, "competent" performance is associated with a less well-connected form of understanding that has some properties of expert understandin g. The labels "non-expert" and "non-competent" simply denote other ways of understanding not currently identified as "expert" or "competent."
In 1982, Strauss and Stavy also outlined a theory of U-shaped development that might appear morphologically similar to this theory. In substance, however, these theories are distinct. For Strauss and Stavy, "Such a [U-shaped] curve indica tes the appearance of a behavior, a later dropping out of that behavior, and what appears to be its subsequent reappearance (p. 1)." This work, in contrast, does not argue that a certain kind of behavior disappears and then reemerges. Instead, it a rgues that the initial behavior of members of a group is structured by one (or more) set(s) of relational ideas and that later behavior becomes structured by other ways of understanding a task. Additionally, U-shaped growth for Strauss and Stavy is a de scription of the time-evolution of performance for individuals. What is articulated herein is a quantitative theory of the distribution and time-evolution (see 6. below) of performance for groups of individuals.
2. The movement of groups of individuals along the range of values (scores on a scale of performance) will not be smooth. Instead, the movement will be characterized by more or less discontinuous jumps between the modes associated with the activity of certain structures or ways of understanding. Boundaries between the modes can be well-defined. Instances of mixed or unstable performance may occur in a data set sometimes. However, these in-between scores are seen to result from an alternation be tween ways of understanding within a performance and do not suggest a separate form of understanding or anything like an average understanding.
3. The bumps will not stand for the same thing. Because understanding is relational and because different relations (structures) draw together qualitatively different kinds of performance, the bumps along an axis of performance will not stand for one kind of thing called understanding (or ability, etc.). Understandings are plural and depend on which kinds of structures or ways of relating elements of a whole are active.
4. What some researchers and educators could see as expert or competent responses to a complex problem (including the responses of competent learners who have jumped) will form an organized whole and will be located as a group at one extreme in a performance evaluation. This placement at an extreme means that there is a good deal of coherence to the expert and competent responses. This coherence can be described quantitatively.
5. Other kinds of responses also will be clustered and potentially well removed from expert or competent performance. Unlike traditional frameworks for discussing "wrong" answers, an analysis of the novice responses reveals a coherence that can be accounted for (ideally) in terms of a relatively small set of active structures (ways of reasoning). The responses can be viewed as the projection of nonexpert ways of understanding onto an axis of expert performance. The image is of similar to that of a mountain range viewed in silhouette. The fact that the mountain peaks appear together does not mean they are linked physically. A silhouette is just a way of looking at what is a multidimensional reality. Despite the fact that they appear on the same performance axis (in the same intellectual silhouette), the modes of a distribution -- like the silhouetted peaks of a mountain range -- may be quite far removed from one another in reality. Within this framework, the most important silhouettes or the most important ways of analyzing understanding are those that best articulate the distinctive peaks in the full range of learners’ thinking. The best assessments are those that help to produce meaningful peaks or that help to articulate of wa ys of thinking present in a group of learners.
6. The time-evolution will be such that the locations of the modes will remain the same even as the size of the populations identified with the modes decreases or increases. As novice understanding shifts to expert or competent understanding, portion s of the population associated with the novice mode will move (jump) to the expert mode (see Figure 6). The relative absence of scores inbetween the modes will be preserved.
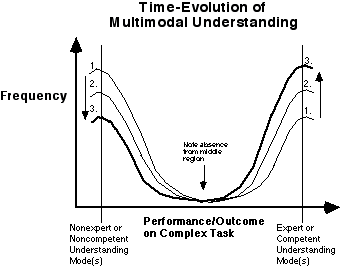
Figure 6. Shifts in population associated with
changing modes of understanding.
In sharp contrast with a normally distributed, multi-modal theory (which might presume that each mode is distributed normally and that the identity of the populations associated with the modes is preserved during a near-continuous sliding along the performance axis), the discontinuous time-evolution described here does not allow for the preservation of the identity of the population associated with any one mode. In a normally distribution, multi-modal theory, the identity of the populations would be preserved and the location of the modes would change. For the alternative theory (and for a given learning domain), the location of the modes is preserved but not the identity of the population associated with each respective mode.
7. A consequence of applying the nonstandard model is that the notion of sample is redefined. Traditionally, the notion of sample means that the researcher is drawing instances from a stable, larger (e.g., that of the population as a whole), sample s pace. For standard parametric sampling, the distribution is presumed to be normal; for nonparametric sampling, the distribution is nonnormal but stable. Formally, this stability means that the integral of the probability density function over an interva l of the domain is presumed to be constant (if unknown). This stability can be preserved under translation (see the sliding of the bump discussed below).
For the nonstandard model outlined above (which, in this respect, is like those found in some areas of quantum physics), this stability cannot be presumed. The shape of the overall distribution is not constant and is determined largely by the circ umstances or context of the experiment or learning tasks. What one is left with are statements about the time-evolution of the chances of finding individual events in certain regions of the sample space. Unlike quantum physics, however, there is no anal ytic model that determines the shape of the density function. We have only the macrophenomena of the relocating population and models of what structures are present that characterize the thinking of learners associated with certain modes.
Limitations of the Nonstandard Methodology
While we have devoted considerable space to the description of a particular nonstandard methodology for assessing group learning, we have not addressed adequately the rendering and assessment of individual learning up to now. There is an implicit relationship between the methodology advanced for groups and an analogous methodology for individuals. In this model, the individual’s location in the intellectual n-space could be characterized and tracked as relatively discrete movement between mo des of thought. In this section, we discuss individual learning and, in so doing, provoke an analysis of some of the limitations of the nonstandard methodology.
Under the proposed nonstandard framework, the space of possible performance is organized in terms of the forms of thinking that the students manifest. It is the organization of this analytic space in terms of the learners’ thoughts, ideas, an d structures, which we consider to be a significant improvement over standard statistical methodologies giving preference to a particular form of averaging (and attendant expectations about distribution). Within the new framework, individuals can relocat e from one form of thinking to others. As a form of assessment, features of performance and understanding typifying populations associated with a particular statistical mode can be seen to typify the understanding of an individual associated with the giv en mode. Expectations about future performance that are associated with a particular mode of thought can be expected to apply to any individual located in that mode (for as long as her or his thought is structured in a certain way).
These aspects of the nonstandard model make it clear that the model addresses the purposes of assessment: to render equivalence classes and address expectations about future performance. We view it as a significant improvement over the current st ate of the art in that the methodology centers on the thinking of learners. A vector in an intellectual n-space does reveal much more about what that person understands than a dimensionless average can. Moreover, this methodology is practicable, it coul d make good use of sophisticated computational capability, and it is capable of informing the activity of the larger educational enterprise.
Despite these very real advances, the methodology outlined earlier does have important limitations. Among the individuals associated with a mode, we fully expect that there would be local diversity not well rendered under the model. Second, the m odel assumes implicitly that the structures are self-contained, do not depend on the path taken to them, and do not retain traces of that path. Not only does this cause problems for the claims of equivalence that we have made for these structures, but al so we would fully expect that these path dependencies and local diversities would manifest themselves in nonequivalent future performance. Lastly, novelty may appear undervalued and even ignored because the expectation might be that learners would move b etween well-established modes in the n-space. We see the last limitation as especially problematic because we do not see novelty as a rarity. Instead, we see novelty manifesting itself regularly at multiple levels of constructive activity: at the level of the learner, all constructions are novel and will be experienced as such; at the level of the n-space, new locations will be created continually; and to the extent that path dependency is taken seriously as an attribute of constructive processes, ther e will be uniqueness with the potential for novel expression in every learner’s cognitive development. Finally, the model also may be problematic in the impression that it gives of the nature and operation of domains; an expectation could be set up that structure would manifest itself in a cross-context way that would ignore the intra-domain, cognitive, and social contextuality of the lived experience of structure.
In the next section, we suggest ways in which new computational technologies can be employed to create richer assessment methodologies that both correspond more closely with constructivist theory and provide a much more detailed and illuminating ac count of learners’ development.
The Coevolution of Technology, Method, and Epistemology
As researchers, we believe that technology, method (or technique), and epistemology coevolve. Constructivism specifically allows that epistemology (including epistemologies that are constructivist) will evolve and that this evolution can be expect ed to happen in relation with the tools and the media of symbolization and activity that we create. For assessment, we believe this means that the epistemological and methodological shifts pointed to earlier need to happen together with the advances in t he technologies that we use to think with and to render our experience. In particular, we hope that with cognitivism free of the need to reduce results to an average, the richness of possibility for rendering associated with increasingly powerful computi ng environments will allow us to look with new eyes and minds at the ways in which we depict what we know of learning. Moreover, with improved communication and networking, assessment can happen now in a way that is close to the fabric of the day-to-day learning activity and not as separate tests.
We close this chapter with a couple of examples of how increasingly sophisticated forms of representation enabled by the technology of the computer might advance this re-vision in our thinking.
The first example is relatively modest in its computing requirements and is most transparent in its links to the theoretical outline given in the previous section. Like the earlier work of Piaget (1946/1970a), it depicts results related to the dev elopment of learners’ understanding of motion. These results are from an investigation of learners’ ideas of how much (amount) and how fast (rate) as they are expressed graphically (Stroup, 1996). A taxonomy was used to encode th e learners’ graphical responses to a series of assessments given at three different times. Then, these responses were compared to the expert responses and the results plotted on an axis of expert performance (see 5. above and Figure 7).
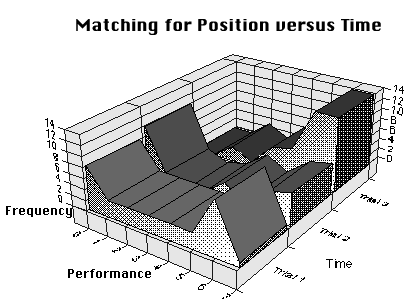
Figure 7. The time-evolution of performance on a matching task.
Figure 7 depicts shifts in understanding of the sort expected under the constructivist model outlined earlier. This general fit is important but so, too, is the fact that the ways of thinking associated with the non-expert modes of thinking can be ide ntified readily and investigated carefully (see Stroup, 1994, 1996). These other forms of understanding are as important to the work of cognitive researchers and educators as are the forms of understanding typically identified as expert or competent. In creasingly sophisticated and nuanced forms of rendering results can be drawn for the purposes of analysis that move well beyond the rather limiting capabilities associated with various parametric statistics.
While the example given above is intended to be illustrative, it does not exhaust the possibilities for the development of cognitivist statistics. A goal for this chapter is to open the door to possibilities and begin a conversation, rather than t o pretend that where this process will end up is already well-formed. Indeed, it is expected that the research community will need to construct and explore the power of new forms of rendering and symbolization of learning. To get a glimpse of where the richness of possibilities could lead, our suggestions include looking to areas of human investigation that deal with making sense of highly complex emergent phenomena. As an example, we are struck by the ways in which weather12 statistics are generated and how the results are depicted using color and dimension in increasingly novel fashion. Weather maps are rich stores of information that capture the current state of the system and enable predictions about future system sta tes (see Figure 8). A map is built up from meaningful attributes of weather systems (temperature, pressure, precipitation, etc.) which, in turn, can be read out of the map and interpreted by a range of users including individual citizens, event planners , city officials, meteorologists, and climatologists. While certain features of the map are arrived at by various forms of averaging, the meaningful attributes (e.g., an isobar or an isotherm) are not aggregated. Pressure is not averaged with temperatur e.
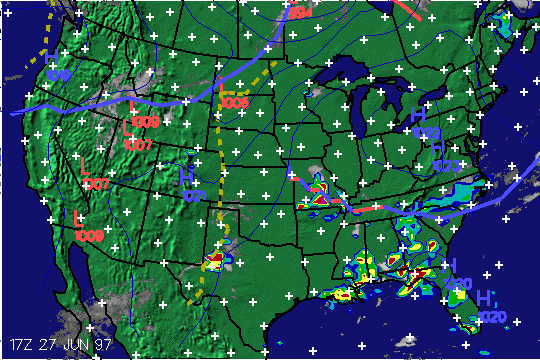
Figure 8. Weather Maps Integrate Complex, Disparate, Information in Ways Can be Interpreted Readily for Different Purposes.
Moreover, the same map can be interpreted in contextually relevant ways. What the map tells and what activities the residents might undertake in different parts of the country are expected to be quite different. Local consumers can make informed d ecisions about what matters to them. The creation and display of such maps make extensive use of sophisticated technological tools. There are rapid advances in the techniques of rendering weather maps with increasingly sophisticated dynamic capabilities t hat the changing weather can be visualized. In turn, these capabilities allow for the exploration and invention of new analytic approaches. The analogue of all of these features, we believe, can be constructed for educational assessment. Assessment should reveal the significant meaningful structures of students’ understanding in ways that could inform future expectations and learning activities. It should not aggregate cognitively meaningful and distinct features of the processes of students’ r easoning. It should serve a range of potential users from classroom educator to district superintendent and beyond. The assessments should be interpretable in different ways across different contexts. We would expect that what a map tells us about them in one context would be quite different from what it tells us about learners in another context. Such maps would enable local educators to make decisions about evaluation without having to default to the norms of a central testing authority. The renderi ng of assessment should be dynamic and interactive in ways that we have come to associate with advanced computational technologies. Maps could display processes spread out over time, highlight specific features, and allow for various degrees of zooming i n and zooming out, enabling educators to see the finely-grained detail of students’ understanding as well as the large-scale summary of the educational system.
The point of including these examples is to highlight the need to push our current sense of possible statistical renderings and symbolizations well past the present state of the art in education. These renderings should center on the ideas of lear ners in a richly situated way. Accordingly, we hope that there is room for a full range of possibilities to be explored before the urge to collapse to standards holds sway. The development of nonstandard statistics or ways of rendering equivalence class es needs to be a jointly constructed effort. As such, the process cannot be seen as one where the outcome is determined in advance.
Notes
1An example of an equivalence class is all students receiving a 5 on a given Advanced Placement examination. The expectation about the future performance of this class of students is that they could perform adequately in subsequent courses in the same domain.
2
Although there seems to be a good deal of confusion about what is meant by structure in the research community, our intended use is close to that articulated in Piaget's Structuralism (1970b) and/or what Seymour Papert calls "powerful ideas" (1980, 1991).
3
"Once the work of clearing away, of groundbreaking, has been done, which consists of discovering new things, and finding things that hadnıt been anticipated, you can begin to standardize --at least if you like that sort of thing -- and to produce accur
ate statistics." (Bringuier, 1980, p.25)
4
"The virtues involved in not knowing are the ones that really count in the long run.... Standardized tests can never, even at their best, tell us anything other than whether a given fact, notion, or ability is already within a childıs repertoire" (Duckw
orth, 1987).
5
Even in this seemingly uncontroversial case, there have been cases of false attributions.
6
Recently, there has been significant literature that questions the assumption of fixed intelligence (see, e.g., Gould, 1993; Dweck & Leggett, 1988; Perkins, 1995).
7
This distinction in the nature of the behavioral object being measured is commonplace in standardized testing. Scholastic Aptitude Tests, for instance, are represented as measuring relatively immovable aptitudes, whereas achievement tests measure relat
ively moveable achievement.
8
For a historical overview, see Statistics in Psychology: An Historical Perspective, by Michael Cowles (1989).
9
Note that structuralist accounts do not need to take a stance regarding the fine structure of learning and knowing in a domain. It is sufficient that an account of such learning and knowing can be given meaningfully through engagement with macrolevel s
tructures . Some cognitivists would trace the emergence of macro- structures to combinations of similar fine-grained structures (see, e.g., Dennett, 1991; Minsky, 1987).
10
There are aspects of Skinnerıs personal theory that many cognitivists would embrace. In particular, it is noncontroversial that some aspects of our internal processing are inaccessible to our introspection.
11
Thomas Kuhn makes this point:
12
We are indebted to Richard Lesh (1996) for suggesting the example of weather.
References Bringuier, J.-C. (1980). Conversations with Jean Piaget. Chicago:
University of Chicago Press. Cai, J., Lane, S., & Jakabcsin, M. S. (1996a) The role of open-ended tasks and ho9listic scoring rubrics: Assessing students’ mathematical reasoning and communication. In P. C. Elliott (Ed.), Communication in mathematics, K-12 and bey
ond (pp. 137-145). Reston, VA: National Council of Teachers of Mathematics. Cai, J., Magone, M. E., Wang, N., & Lane, S. (1996b). Describing student performance qualitatively. Mathematics Teaching in the Middle School, 1, 928-835. Cowles, M. (1989). Statistics in psychology: An historical perspective . Hillsdale NJ:
Lawrence Erlbaum
Associates[T]he Ptolemaic system...was admirably successful in predicting the changing positions of both stars and planets. No other ancient system had performed so well; for the stars, Ptolemaic astronomy is still widely used today as an engineering
approximation; for the planets, Ptolemyıs predictions were as good as Copernicusı. (Kuhn, 1962/1970, p. 68).
Dennett, D. (1991). Consciousness explained. Boston, MA: Little Brown & Co.
Duckworth, E. (1987). The having of wonderful ideas and other essays on teaching and learning. New York: Teachers College Press.
Dweck, C. S. & Leggett, E. L. (1988). A social-cognitive approach to motivation and personality, Psychological Review, 95(2), 256-273.
Feldman, D. (1980). Beyond universals in cognitive development . Norwood, NJ: Ablex Publishers.
Gardner, H. (1989). To open minds . New York: Basic Books, Inc.
Gardner, P. L. (1975). Scales and statistics. Review of Educational Research, 45(1), 43-57.
Glass, G., Peckham, P., & Sanders, J. R. (1972). Consequences of failure to meet assumptions underlying the fixed effects analysis of variance and covariance. Review of Educational Research, 42, 237-288.
Gould, S. J. (1993). The Mismeasure of Man. W.W. Norton & Co, New York.
Heidelberger, M. (1987). Fechner’s Indeterminism: From Freedom to Laws of Chance. In L. Kruger, L. Daston, & M. Heidelberger (Eds.), The Probabilistic Revolution, Vol. 2, Cambridge, MA: MIT Press.
Kilpatrick, J. (1978). Research on problem solving in mathematics. School, Science, and Mathematics, 78(3), 189-192.
Köhler, W. (1959). Gestalt psychology: An Introduction to new concepts in modern psychology . New York: Mentor.
Kuhn, T. S. (1957). The Copernican revolution . Cambridge, MA: Harvard University Press.
Kuhn, T. S. (1970). The Structure of Scientific Revolutions . Chicago: The University of Chicago Press. (Original work published 1962).
Lambdin, D. V., Kehle, P. E. & Preston, R. V. (Eds.). (1996) Emphasis on assessment: Readings from NCTM’s school-based journals. Reston, VA: National Council of Teachers of Mathematics.
Mathematical Sciences Education Board, National Research Council. (1993). Measuring up: Prototypes for mathematics assessment. Washington, DC: National Academy Press.
Mathematical Sciences Education Board, National Research Council. (1993). Measuring what counts: A conceptual guide for mathematics assessment. Washington, DC: National Academy Press.
Meltzer, L (1994). New directions in the assessment of students with special needs: The Shift toward a constructivist perspective. Journal of Special Education. Vol 28(3)
Micceri, T. (1989). The unicorn, the normal curve, and other improbable creatures. Psychological Bulletin, 105(1), 156-166.
Minsky, (1987). The Society of Mind. Simon & Schuster Inc., New York.
National Council of Teachers of Mathematics (1989). Curriculum and evaluation wtandards for school mathematics. Reston, Va: National Council of Teachers of Mathematics (NCTM).
National Council of Teachers of Mathematics (1992a). Alternative assessment [Theme issue]. Mathematics Teacher, 85(8).
National Council of Teachers of Mathematics (1992b). Alternative assessment [Focus issue]. Arithmetic Teacher, 85(8).
National Council of Teachers of Mathematics (1995). Assessment standards for school mathematics [K—12]. Reston, Va: NCTM.
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.
Papert, S. (1991). Situating constructionism. In I. Harel & S. Papert (Eds.), Constructionism. Norwood, NJ: Ablex.
Perkins, D. N. (1995). Outsmarting IQ: The emerging science of learnable intelligence. New York: Free Press
Piaget, J. (1970). The Child's conception of movement and speed . New York: Basic Books, Inc. (Original work published in 1946).
Piaget, J. (1970). Structuralism . New York: Basic Books.
Sawilowsky, S. (1990). Nonparametric Tests of Interaction in Experimental Design. Review of Educational Research, 60(1), 91-126.
Schoenfeld, A. H. (1987). Cognitive science and mathematics education: An overview. In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education. Hillsdale, N J: Lawrence Erlbaum.
Siegel, S. (1956). Non-parametric statistics for the behavioral sciences . New York: McGraw-Hill.
Skinner, B. F. (1968). The technology of teaching. Englewood Cliffs, NJ: Prentice-Hall, Inc.
Skinner, B. F. (1978). Reflections on behaviorism and society . Englewood Cliffs, NJ: Prentice-Hall.
Stevens, S. S. (1946). On the theory of scales of measurement. Science, 103, 677-680.
Stevens, S. S. (1951). Handbook of experimental psychology. New York: Wiley.
Strauss, S., & Stavy, R. (1982). U-shaped behavioral growth. New York: Academic Press.
Stroup, W. (1994). What the development of non-universal understanding looks like: An investigation of results from a series of qualitative calculus assessments. Technical Report No. TR94-1. Cambridge MA: Harvar d University, Educational Technology Center.
Stroup, W. (1996) Embodying a nominalist constructivism: Making graphical sense of learning the calculus of how much and how fast. Unpublished doctoral dissertation, Harvard University, Cambridge MA.
Swijtink, D. (1987). The objectification of observation: Measurement and statistical methods in the nineteenth century. In Kruger, L. Daston, L. & Heidelberger, M. (Eds.), The Probabilistic Revolution, Vol. 2, Cambridge, MA: MIT Press.
Vermont Department of Education. (1991). Looking beyond "the answer": The report of Vermont’s mathematics portfolio assessment program. Montpelier, VT.
Wilensky, U. (1991). Abstract meditations on the concrete and concrete implications for mathematics education. In I. Harel, & S. Papert (Ed.), Constructionism. Norwood NJ: Ablex. Chapter 10. pp. 193-203.
Wilensky, U. (1993). Connected mathematics: building concrete relationships with mathematical knowledge. Unpublished doctoral dissertation, Massachusetts Institute of Technology, Cambridge MA.
Wilensky, U. (1995). Paradox, Programming and Learning Probability. Journal of Mathematical Behavior. Vol. 14, No. 2. p 231-280
Wilensky, U. (1997). What is Normal Anyway? Therapy for Epistemological Anxiety. Educational Studies in Mathematics. [Special Issue on Computational Environments in Mathematics Education] Noss R. (Ed.) Volume 33, No. 2. pp. 171-202