Thinking like a Wolf, a Sheep or a Firefly: Learning Biology through Constructing and Testing Computational Theories -- an Embodied Modeling Approach

Center for Connected Learning and Computer-Based Modeling
Northwestern University
Annenberg Hall 311
2120 Campus Drive
evanston, IL 60208
847-467-3818

Abstract

Biological phenomena can be investigated at multiple levels, from the molecular, to the cellular to the organismic to the ecological level. In typical biology instruction, these levels have been segregated. Yet, it is by examining the connections between such levels that many phenomena in biology, and complex systems in general, are best explained. In this paper, we describe a computational approach that enables students to investigate the relations between different biological levels. Using object-based parallel, embodied modeling tools, students model the micro-rules that underlie the emergence of a phenomenon, and then observe the aggregate dynamics that result. This approach has been developed as part of the "Making Sense of Complex Phenomena" Project (MSCP). We describe two extended examples from MSCP in which this approach was employed: predator-prey relationships and synchronously flashing fireflies. In the first example, the topic of predator prey relations is familiar to students and can be treated by classical methods. We argue that the embodied modeling approach connects more directly to students’ experience and allows for extended investigations and deeper understanding. In the second example, the topic of firefly flash synchronization does not readily yield to classical approaches and is, thus, unfamiliar to students. As such, the embodied modeling approach allows this topic to be productively introduced into the high school curriculum. In both cases, students can frame hypotheses related to their questions, construct computer models that incorporate these hypotheses, and test their hypotheses by running their models and observing the outcomes.

1.0 Introduction

The contrast between the processes in which these two communities are engaged leads biology students to form a misleading picture of the biological research enterprise. Students form beliefs that biology is a discipline in which observation and classification dominate and reasoning about theories is rare. Furthermore, they believe that learning biology consists of absorbing the theories of experts and that constructing and testing their own theories is out of reach.¹

In this paper, we present an approach that attempts to narrow the gap between school biology and research biology. The approach centers on the use of innovative computer modeling tools that enable students to learn biology through processes of constructing and testing theories.

In recent years, several educational research projects (Jackson et al, 1996; Ogborn, in press; Roberts et al, 1983, 1988) have employed computer modeling tools in science instruction. The approach taken herein differs from these approaches in its use of object-based modeling languages that enable students to model biological elements at the level of the individual (e.g., individual wolf/sheep) as opposed to aggregate (differential-equation based) modeling languages that model at the level of the population (wolf/sheep populations) (Chen and Stroup, 1993). This technical advance in modeling languages enables students to employ their knowledge of the behavior of individual organisms (or molecules, cells, genes..) in the construction of theories about the behavior of populations of organisms. Furthermore, the ability to model individual behavior enables students to employ their personal experience with sensing and locomoting in the world as initial elements in their models of other organisms. In this way, the well known tendency of children to explain biological behavior through personification (see e.g., Carey, 1986; Hatano & Inagaki, 1987), instead of being seen as a misconception or a limitation to be overcome, becomes a building block towards the construction and refinement of plausible biological explanations.²

In previous work, the authors and other object-based modeling projects (Repenning, 1994; Resnick, 1994; Smith et al, 1994; Wilensky, 1995; in press; Wilensky & Resnick, 1999) have described the approach in a broad inter-disciplinary context. In this paper, we explore the use of this approach, specifically, in biology instruction.

1.1 Mathematical Biology and Computer-Based Modeling in the Field and in the Classroom

The gap between school biology and research biology can be partially explained by a lag in the transfer of newer biological methods to the school setting. Indeed, at all levels from the molecular to the ecological, the science of biology has undergone an important shift over the last century. As biologists have increasingly availed themselves of the language of dynamic systems to model natural phenomena, biology once an entirely qualitative discipline has become more quantitative.³ Mathematical models have added precision to biological theories, increased their predictive power, and have been important sources of explanations and hypotheses. The generation and refinement of such models has become a pervasive element of modern biological inquiry. Yet, despite this virtual revolution in biology practice, the high school and undergraduate biology curriculum have scarcely noticed. For most secondary and post-secondary biology students, the study of biology remains primarily an exercise in memorization. Due to the formidable mathematical prerequisites that quantitative models have traditionally imposed, students below the advanced undergraduate level are given little or no exposure either to dynamic models or to the modeling process. The computational approach presented here enables us to give students this exposure, while sidestepping the traditional mathematical roadblocks.

We begin, in the following section, by describing our "embodied" approach to biological modeling and the object-based parallel modeling language, StarLogoT, in which the models are constructed. In section three, we illustrate this approach and contrast it with classical modeling techniques by developing both embodied and classical models of predator-prey population fluctuations. We follow a high school student, Talia, in her efforts to create embodied models of wolf-sheep predation. In section four, we follow another student, Paul, as he develops a computational model of synchronously flashing fireflies (these species of fireflies are prevalent in the far east, especially Thailand). In contrast to the topic of predator-prey population dynamics, the firefly flash synchronization problem does not easily admit classical approaches and is, thus, unfamiliar to students. We use this example to frame a discussion of the student modeling process and the relationship of this process to modeling within science. Finally, in our concluding remarks we respond to criticism of our approach and summarize the major points of the paper.

1.2 Research Settings

The student modelers described below were participants in the "Connected Mathematics" (Wilensky, 1993; 1995) and, principally, the "Making sense of Complex Phenomena" (MSCP) (Wilensky, 1997; in press) projects in which students learn about complex systems through construction of object-based parallel models of these systems. The goal of the MSCP project is to construct computational toolkits that enable students to construct models of complex systems and to study students engaged in using these toolkits to model complex systems and to make sense of their behavioral dynamics. Research has documented the difficulties people have in making sense of emergent phenomena, global patterns that arise from distributed interactions, central to the study of complex systems. We have labeled the constellation of difficulties in understanding emergent phenomena and constructing distributed explanations of such phenomena the deterministic/centralized mindset (Resnick & Wilensky, 1993; Wilensky & Resnick, 1995, 1999; Resnick, 1996). In the MSCP project we have worked with a wide variety of students, ranging from middle school students to graduate student researchers as well as both pre-service and in-service teachers on moving beyond this mindset to a richer understanding of the dynamics of complex systems. The primary research sites are two urban Boston high schools. Students from these schools participated in the project as part of their classroom work. Undergraduates and pre-service teachers participated in the context of teacher education courses at Tufts University. Some students participated through informal contexts, pursuing modeling investigations in after-school settings or at the laboratory, housed at the project cite, the Center for Connected Learning and Computer-Based Modeling at Tufts University. In the classroom context, students, typically, were involved in an extended classroom modeling project led by the classroom teacher and assisted by project researchers. The role of the researchers was to document student work through videotaping and field notes and to support students and teachers in the use of project materials and modeling languages. Such support included the dissemination of interesting cases to be potential sources of models, bringing in books and web sites that might be useful to the modelers. Project researchers also engaged students in structured activities (including participatory simulations not involving the computer (Resnick & Wilensky, 1998)) that would foster reflection on the concept of emergence. They also provided support to students and teachers on the syntax of the modeling language. The computational models described in this paper were built in an object-based parallel modeling language called StarLogoT (Resnick, 1994, 1996; Wilensky, 1995, in press). In the next section, we describe the workings of StarLogoT and its advantages for modeling biological phenomena.

2.0 The StarLogoT Modeling Language

StarLogoT derives from, and has contributed to, recent work in the field of complex systems. This field studies the dynamics of systems that are constituted by many interacting elements. Taken as a whole, the behavior of these systems can be extremely complex and difficult to predict, though their individual elements may be quite simple. Examples can be found in many fields, from physics and chemistry to economics and political science, and biology has been a particularly fertile domain of complex systems oriented research (Langton, 1993; Kauffman, 1995). Though the brain, the immune system, and the behavior of organisms such as ants or bees are all oft-cited examples, in fact, nearly all of biology can be considered from this perspective. Genetic and cellular processes can be viewed as the complex outcomes from molecular interactions, organisms and their organs can be viewed as the complex outcomes from cellular and genetic level interactions, and ecological systems can be viewed as the complex outcomes of interactions between individual organisms. Of course, there is causality in the other direction as well; organism behavior can effect cellular and genetic level activity, and ecological circumstances can effect the behavior of individuals. Indeed, what makes complex systems so difficult to study is that aggregate level structures can have feedback effects on the behavior of the elements of which they are composed.

StarLogoT is a general-purpose (domain independent) modeling language that facilitates the modeling of complex systems. It works by providing the modeler with a framework to represent the basic elements the smallest constituents of a system, and then provides a way to simulate the interactions between these elements. With StarLogoT, students write rules for hundreds or thousands of these basic elements specifying how they should behave and interact with one another. These individual elements are referred to as ‘turtles’. (StarLogoT owes the ‘turtle’ object to the Logo computer language). Turtles are situated on a two dimensional grid on which they can move around. Each cell on the grid is called a ‘patch’, and patches may also execute instructions and interact with turtles and other patches. Some typical commands for a turtle are, to move in a given direction, to change color, to set a variable according to some value, to "hatch" new turtles, or to look at the properties (variables) of other turtles. Turtles can also generate random values, so that they can, for example, execute a sequence of commands with a fixed probability. Patches can execute similar commands, though they cannot change location. The wide range of commands executable by turtles and patches makes it possible to use them to represent many different systems. For example, turtles can be made to represent molecules, cells, or individual organisms, while patches can represent the medium (whatever it may be) in which they interact.

Dynamic modeling tools, such as StarLogoT, are used to represent changes in the states of systems over time. In StarLogoT, time is represented as a discrete sequence of ‘clock-ticks’. At each clock-tick, each turtle and patch is called upon to execute the rules that have been written for it. Students need not write separate rules for each turtle (or patch) the power of StarLogoT comes from the fact that all turtles can execute the very same set of rules at each clock-tick. If all turtles are executing the same rules, won’t their collective behavior be repetitive and uninteresting? To see why this is not the case, it is important to take note of the fact that even though two turtles might be following the same rules, their behavior could be markedly different. This is because the two turtles may have quite different internal properties and be situated in dissimilar environments. For example, the turtles may be following the rule "if you smell food ahead, move forward a distance equal to your body length. Otherwise, turn around". If one turtle is in the vicinity of food, it will move forward, the other turtle, far from the food, will turn around. Even if they are both in the vicinity of food, and even in the exact same location, if they have different body measurements, they will move to different locations. It is this diversity in internal states and in surrounding environs that enables the collective turtle behaviors to admit a surprising degree of variance.

The modeling approach we describe instantiating the individual elements of a system and simulating their interactions is not unique to StarLogoT. Such models have been used across a wide variety of domains and have been referred to by many different labels such as: object-based parallel models (Wilensky, 1995; 1997) agent-based models (Beer, 1990; Maes, 1990; Repenning, 1993; Epstein & Axtell, 1996), individual-based models (Huston, 1988; Judson, 1994), and particle simulations (Buneman et al, 1980). These "new wave" modeling approaches have transformed biology research practice enabling researchers to model increasingly complex multi-leveled biological systems (Forrest, 1989; Langton, 1994; Keen & Spain, 1990; Taylor et al, 1989). For the remainder of this paper, we will employ the term 'embodied modeling' to refer to this general approach . While the term, "object-based parallel modeling", which we have used in the past is, perhaps, a more accurate description of the technical workings of StarLogoT, the "embodied modeling" label more closely matches the experience of a biology modeler who is actively engaged in understanding and embodying the behavior of individual biological elements.

In the following two sections of the paper, we will illustrate the embodied modeling approach in biology with two extended examples of modeling biological phenomena. We intend these examples to illustrate both how such an approach can 1) facilitate the creation and verification of predictive multi-level models in biology and 2) enable biology students to create more powerful explanations of and deepen their understanding of biological phenomena.

3.0 Modeling Predator-Prey Population Dynamics⁴

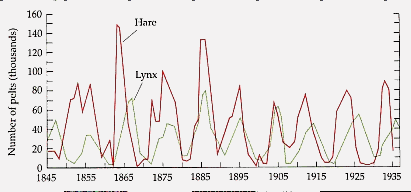
The dynamics of interacting populations of predators and their prey have long been a topic of interest in population biology. Comparisons of a number of case studies have revealed similar dynamics between such populations, regardless of the specific species under study and the details of their interactions. (Elton, 1966). Notably, when the sizes of the predator and prey populations are compared over many generations, we tend to find regular oscillations in these sizes which are out of phase; where one increases, the other tends to decline, and vice-versa (see figure 1). Numerous mathematical models have been proposed to explain these oscillations. In this section, we will examine several StarLogoT models that are at considerable variance from classical versions. Along with providing a first-hand glimpse of our approach to modeling systems, the example will also allow us to contrast the different perspectives promoted by embodied versus classical tools. We begin with a look at a well-known classical model.

Figure 1. Fluctuations of the sizes of predatory lynx and prey hare populations in Northern Canada from 1845-1935 (from Purves et al, 1992).

3.1 The classical approach

For many years, models of predation were based on the Lotka-Volterra (Lotka, 1925; Volterra, 1926) model.⁵ Alfred Lotka and Vito Volterra (working independently from each other) were among the first to carry over to biology differential equation models, previously employed principally in physics and chemistry. The Lotka-Volterra model of predation works by specifying interactions between the predator and prey populations framed as a set of coupled differential equations. Each such equation describes the rate at which a given variable (e.g., the density of the prey population) changes over time. Here we present the Lotka-Volterra predation equations, which describe changes in the densities of the prey population (N1) and the predator population (N2). Keep in mind that population size and population density are proportional to one another.

dN1/dt = b1N1 - k1N1N2 (1)

dN2/dt = k2N1N2 - d2N2 (2)

In these equations b1 is the birth rate of the prey, d2 is the death rate of the predators, and k1 and k2 are constants.

Let us briefly analyze (1). There are two terms in the equation. In the first term (b1N1), the prey birth rate is multiplied by the density of the prey population, yielding the increase in density due to new prey births. In the second term (k1N1N2), the frequency of interaction between the prey and predator populations is determined, yielding the decrease in prey density due to consumption of prey by predators. The rate of change in the density of the prey population is thus computed by subtracting the total effect of prey deaths from the total effect of prey births. (2) can be analyzed along similar lines, although in this equation predator births are dependent on the frequency of predator-prey interactions, while predator deaths are not a reversal from (1).

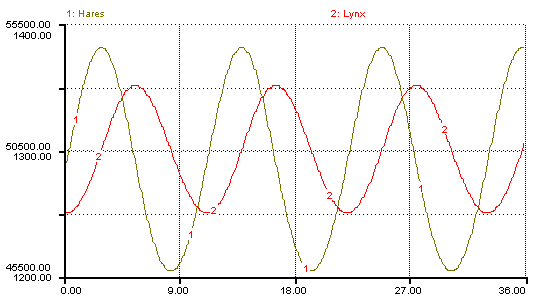
It is important to notice that (1), which describes the prey population, contains N2, the variable describing the density of the predator population, and vice-versa. The equations thus specify how the density (and so size) of each population depends on the density of the other. Specifically, increases in the prey population will cause the predator birth rate to rise, and increases in the predator population cause the prey death rate to rise. A typical plot produced from these equations is shown in figure 2. Indeed, we see here the characteristic cyclical fluctuations between the predator and prey populations.

Figure 2. Results of Lotka-Volterra predation model for Lynx and Hare with respective initial populations of 1250 and 50,000.

We need not go into further depth about these equations. The point to notice for now is that the classical approach describes the cyclical fluctuations between predator and prey populations by specifying relationships between population-level properties, such as birth rate, frequency of interaction, and overall density.

3.2 The embodied approach

Using embodied tools, such as StarLogoT, we approach this problem from a different angle. Rather than describe relationships between properties of populations, we are concerned primarily with specifying the behavior of individuals. The relevant question here is, what kinds of actions must an individual predator or individual prey follow so that populations of such individuals will exhibit the characteristic oscillations? Another way to think about the actions of individuals the method behind StarLogoT modeling is to consider the rules that each organism might follow in order for the given population-level patterns to result.

There are a number of paths that a modeler might take towards finding such a set of rules (indeed, there are often a number of equally effective solutions). It may seem to readers that one would need to be highly familiar with the phenomenon being modeled and with current theories in order to make meaningful progress, but our experience indicates otherwise. In the Making Sense of Complex Phenomena project, we have found that students are often able to develop solid explanatory models of various phenomena, with only a small amount of background knowledge. We generally encourage modelers to try and make sense of a problem on their own before seeking external resources, and often they are quite surprised at how far they are able to get. Rather than quickly reaching for the "facts", students undertake something akin to a scientific inquiry, and generally learn much more than if someone had simply given them the solution. Of course, the body of existing research is quite important to the development of a model, and StarLogoT modelers will often go back and forth between developing new hypotheses and researching existing solutions. To help convey a sense of this process, we will describe the development of a StarLogoT predation model from the standpoint of a student, Talia. In reality, Talia is a composite of several student modelers that participated in the Making Sense of Complex Phenomena project.

3.3 Finding rules for wolves - an initial model

Talia’s task was to formulate a plausible set of rules for a predator and a prey. Recall that the characteristic properties of predator-prey population dynamics have been observed to be strongly similar across many species and many different conditions. Rather then be specific, then, these rules needed to point to general behaviors that all such species perform in one way or another. In her first attempt, she described a predator (say, a wolf) as moving about in the StarLogoT world and looking for prey (say, sheep). As a real wolf needs energy to live, she decided that each step in the world should cost the model wolf energy. Running out of energy will cause the wolf to die, and the only way to gain energy is by eating sheep. In this way, Talia was, also, like the Lotka-Volterra model above, describing a dependency between predators and prey: wolves are likely to persist when sheep are abundant (because they are unlikely to run out of food/energy), and sheep are expected to die when wolves are abundant (because they will eventually be eaten). Here, then, is a simple rule-set for a wolf based on the Talia’s initial description:⁶

Talia decided on a simpler rule-set for the sheep. They only move about and reproduce, though they risk being eaten by the wolves:

Notice that the mechanism for reproduction in Talia’s model is blind probability; any wolf or sheep may reproduce at a given clock-tick if the numbers come up right. This may seem like she was cheating, for surely this is an unrealistic way to portray behavior at the individual level. Talia had firm a justification for this though. She reasoned that there are many different ways in which various organisms reproduce, and yet, similar dynamics tend to arise in populations regardless of the specific reproductive mechanisms. To keep the model as general as possible, she adopted a probabilistic rule that effectively says "reproduce every now and then". This allowed her to achieve the desired behavior without being specific about mechanisms.

Of course, mechanisms are important to embodied models, and they generally are specified. The rules governing death in this model, for example, are more specific than those for reproduction: prey die specifically when they are eaten by predators, and predators die specifically by running out of food. Wherever the particular mechanism is relevant to the model it should be included, otherwise details in the model can be minimized using probabilistic rules.

To be sure, there are many simplifications made by Talia’s model that are questionable. A quick list includes: only a single factor limiting the growth of predators (starvation), only a single factor limiting the growth of prey (they are eaten), random movement, no limit on number of organisms on a single patch, only two dimensions, etc. It is certainly possible, even likely, that these are not just simplifications, but oversimplifications. There is no quick way to determine where such abstractions are valid and where they are mistaken. This uncertainty, though, is an integral part of the process of modeling not only with embodied models, but with any scientific modeling process. The modeler must carefully consider which kinds of simplifications are plausible, and, even then, it is often only repeated testing of the model and revision of the assumptions that may ultimately lead to a working model.

Once Talia had completed the coding of her model in the StarLogoT language, she selected values for each of the parameters in the model (i.e., E1, E2, R1, R2, the initial number of wolves and sheep, and the length and width of the patch world). The values of model parameters, initially set by intuition, will often have a significant effect on the outcome of a StarLogoT simulation. The modeler may induce what kind of effects, if any, each parameter has on the outcome by repeatedly altering these parameters and observing the result. Since the relation between the various parameters of a model can be non-linear, this can be, not surprisingly, a difficult task.

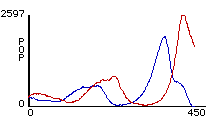
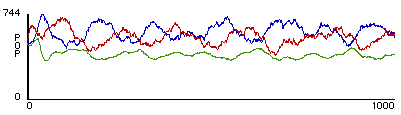
After Talia ran her model several times under various parameter configurations, she noted that one of two general outcomes would always result. Most often, there were oscillations until all the sheep were eaten, whereupon the wolves died from starvation (figure 3a). Sometimes usually under low density parameters (e.g., small population size or narrow screen width) there were oscillations until the number of sheep dipped too low and the wolves all died off, at which point the sheep population increased at an exponential rate (figure 3b). Thus, Talia's rule-set successfully produced population oscillations, but this pattern was consistently transient and unstable. These results were clearly not in line with the sustained population oscillations observed in nature and those of the Lotka-Volterra model. The next logical step in the modeling process was for her to revise her thinking.

Figures 3a.(left) and 3b (right). Two different outcomes from rule-sets W1 + S1. Red lines represent predator population size and blue lines represents prey population size.

3.4 Revising the model

Talia was initially disturbed to find that her model did not meet her expectations. Still, she was determined to create a version that exhibited a stable relationship between the wolf and sheep populations. That is, one where the two populations would continue to coexist, despite ongoing fluctuations in size. To generate such a version, she put great effort into understanding the behavior of her existing model. She asked herself: Why did the populations crash? What factors might be missing or misrepresented? From analyzing plots such as figures 3a and 3b, she was led to several observations concerning the stability of her model. (1) The peaks of the wolves follow peaks of the sheep. (2) The higher the peaks of the sheep, the higher the peaks of the wolves. (3) The higher the peak, the deeper the following crash. Instability in the model appeared to manifest itself in the ever-increasing amplitude of the population oscillations. The peaks get higher and the crashes get deeper over time, until zero is reached and the cycle ends altogether. What she decided to search for, then, were factors to help limit the amplitude. That is, factors to help contain both uncontrolled growth and uncontrolled decline in the sizes of the populations. In the course of further examining the model and its behavior, Talia devised a number of theories about the reason for the observed instability. She tested her theories through a process of successive revision, where she would repeatedly devise a corresponding variation to her rule-set, instantiate it in StarLogoT, and observe its effects.

3.4.1 Discussion: The danger of curve-fitting

This activity of successive model revision is useful in that it allows students experience in developing original hypotheses, in formalizing them, and, to some degree, in testing them out. Modelers engaged in the process of model revision need to be aware of a potential danger: In attempting to alter a model in order to achieve a certain desired result, they run the risk of ‘curve-fitting’. That is, they may end up with a model that bears superficial similarity to the system that they are trying to model, but achieves this using an unrelated mechanism. This danger occurs whenever there is a target behavior for a model, and once the target behavior is achieved, the model is not subjected to further testing in order to assure a genuine correspondence. In general, embodied models are less prone to this danger than classical models, for they model systems at two levels (underlying mechanisms, and global behavior), rather than just one (global behavior). This two-tier approach is safer, because there are more constraints that the modeler must satisfy (we will elaborate on this in section 3.4.3). However, when modelers are not critical of the plausibility of their assumptions, the problem of superficial correspondence remains an acute danger. To avoid this hazard, students should always focus on the plausibility of the model as a whole rather than only on its behavior. For example, when the results of a model are not in line with expectations, a student should ask, "what have I missed about the behavior of the components?" not simply, "how can I change my model to make it behave the way I want it to?"

3.4.2 Researching the relevant biological literature

Research into scientific literature is often a part of the debugging process. This can help amend any errors in a student’s knowledge of the phenomenon or reveal any important facts that she might be overlooking. After experiencing difficulty devising a rule-set that would lead to stable oscillations, Talia decided to do some research to determine the source of the problem. She discovered a substantial base of scientific literature addressing experimental evidence and theory of two species predator-prey systems. Notably, she read that when such systems were first created in the laboratory by G. F. Gause, the findings were just as with her StarLogoT model: either the predators ate all the prey and then starved, or, under certain conditions, the predators first died, and then the prey multiplied to the carrying capacity of the environment (Gause, 1934). Gause was surprised at this result based on the work of Lotka and Volterra, he fully expected such two-species systems to be inherently stable. Thus, Talia thus learned, to her surprise that her model wasn’t necessarily wrong at all it was the Lotka-Volterra model that was mistaken!

Talia’s model failed to reproduce the dynamics of predator-prey systems found in nature, but it succeeded in predicting the dynamics that have been observed in the laboratory. Her research uncovered two important differences between the natural and experimental settings to account for this discrepancy. First, is the lack of constraints on the growth of the prey population in the experimental settings. In nature, the size and rate of growth of the prey population are constrained by several factors, including limits on the food resources available to prey and limits on their maximum density. The laboratory experiments, however, included abundant food for the prey, and no other adversities in the system but the possibility of predation (Luckinbill, 1973). Second, is in the lack of environmental complexity the models and the experiments leave no place for the prey to seek refuge and evade the predators, thus preempting the possibility of having some sub-populations of prey surviving in different regions (Huffaker, 1958).

3.4.3 Discussion: Contrasting embodied versus classical assumptions

Talia’s model did not produce the expected results, but it turns out that this is only because her expectations were mistaken. The model omits any rules pertaining to environmental conditions or limits on food for prey, and thus it correctly predicts the outcome of the laboratory situation, which also omits these factors. The Lotka-Volterra model does not include these factors either, and given this, we would expect it to offer predictions for the experimental condition, not the natural condition. Indeed, Lotka and Volterra thought that their equations constituted a mathematical proof that such two species predator-prey systems are inherently stable. Instead, this prediction has been shown false. Why might the two models differ in this way?

One might initially think that the different predictions offered by these two models can be attributed solely to skill (or luck) on Talia’s part. In fact, neither skill nor luck can explain this alone she tried very hard to achieve Lotka-Volterra-like behavior using StarLogoT, but was unable to do so without significant changes to her assumptions. This suggests that the factor that best accounts for her success versus Lotka’s and Volterra’s failure in this particular case was her use of embodied modeling tools.

Classical tools prevail in modern scientific practice because they provide, in many cases, an extremely concise and accurate representation of a system. Nevertheless, these tools need to be applied with great care. Compared with embodied tools, classical tools make it much easier to model aggregate-level outcomes that are biologically implausible. Recall that that classical and embodied tools each incorporate assumptions at different levels the former at the aggregate level, and the latter at the individual level. This is no small point. While classical tools allow us to make any aggregate-level assumptions we want, embodied tools do not allow us to make any aggregate assumptions at all. Instead, we must code our assumptions at the individual level, and wait to see what the logical, aggregate-level consequences of these are. Depending on the outcome we have in mind, it may be that a reasonable individual level rule-set with this outcome simply does not exist.

It is still possible to make mistaken assumptions at the individual level, but there are two reasons why these may be easier to detect in embodied models than in classical ones. First, embodied models offer more feedback to the modeler; there are two levels at which to debug them, rather than only one level at which to debug classical models. We can scrutinize both the plausibility of the individual-level assumptions as well as the plausibility of the resulting aggregate-level outcomes. If either seem suspicious, then we have a hint that we may be on the wrong track. With classical tools, the only assumptions are, generally speaking, aggregate-level assumptions, so new information isn't typically gained from observing a model’s outcome.

The second reason why mistaken assumptions may be easier to detect in embodied models is that they take the form of rules for action. We have found that most students are already accustomed to thinking in terms of such rules, simply by analogy to their own experience. Hence, they come equipped with intuitive strategies for understanding and developing embodied models. For example, students will often try to make sense of a given rule-set by assuming the perspective of the individuals within the model and using their imaginations. Classical models, in contrast, require students to think in terms of abstract quantities, such as rates and population densities. While thinking in this mode may be comfortable for professional mathematicians, it is quite foreign to most students.

3.4.4 Discussion: Contrasting embodied versus classical explanations

Embodied models have another advantage over classical models that is particularly relevant in an educational setting. This is that embodied models not only represent processes, but also the mechanisms that underlie them. A classical model describes no more than a quantitative pattern: the Lotka-Volterra model describes a set of two curves. The explanation that it offers for these curves could be called a shallow one. It accounts for them by explaining that the birth rate of the predators is proportional to the number of prey, and that the death rate of the prey is proportional to the number of predators. We call this shallow, because it is never actually specified how this explanation relates to actual organisms. In fact, this explanation can be induced just from looking at the population plots themselves the very same plots we are trying to explain! Often when we ask for an explanation, though, we are looking for an underlying cause. That is, not an account of the pattern itself, but an account of the mechanism that gives rise to it. This deep kind of explanation, often more satisfying to students, is precisely what embodied models provide (Reisman, 1998; Wilensky, 1997, in press).

By bridging events with their underlying causes, deep explanations allow students to form powerful conceptual connections between their understanding of phenomena at different levels (see Wilensky & Resnick, 1999). Currently, most topics in biology (and in science, in general) are taught only at a single level. Be it the molecular, cellular, anatomic, organismic or ecological levels, these topics tend to be conveyed and understood in isolation from one another. It is unfortunate that the relations between these levels are not typically emphasized, given the possibility for topics at each level to provide deep, mechanistic explanations for topics at adjacent levels up. For example, students can apply their knowledge of molecules in order to make better sense of cellular processes, and apply their knowledge of organisms in order to make better sense of ecological processes. Not only does this provide a stronger intuitive basis for students to understand each topic, but it may unify their understanding of biology as a whole. Though computer tools are certainly not required in order to emphasize these conceptual connections between topics many teachers already stress such connections to great effect in their lectures our experience has shown StarLogoT modeling to be a particularly effective means.

3.4.5 Adding grass greater complexity can promote stability

Both the classical and embodied models presented above require emendation to account for the experimental findings. Many accurate classical models of predation have been developed since the work of Lotka and Volterra, but their mathematical complexity is beyond the scope of this paper, and surely beyond the reach of most undergraduates (let alone high-school students). We now turn to an alternative rule-set that Talia devised in order to prevent her StarLogoT ecosystem from destabilizing.

Talia learned that a major disparity between Gause's experimental setup and the natural case studies was the lack of constraints on the growth of the prey population. In natural systems, the prey population is generally constrained by the amount of resources available in the environment (e.g., food and living space) so that there is effectively a carrying capacity a maximum number of organisms that can be supported that limits the growth of the population. Gause’s experimental setup and Talia’s model both overlook this, and instead include no such limits to growth. Prey within both systems have, at all times, ample food and ample space in which to live. As it turns out, surprisingly perhaps, this makes a significant difference to the stability of the system.

In order to impose a carrying capacity on the sheep population, Talia decided to modify her model so that sheep would now be required to consume some limited resource in order to survive. The new model would now include not only wolves and sheep, but also grass, which would "grow" back once eaten. She represented the grass by means of patches that could either be green (i.e., grass available for consumption) or brown (i.e., grass has already been consumed). Once a patch would turn brown, it would begin a countdown and only revert to green after some fixed interval of time. There were then two ways the prey could die either by being eaten or by starving. These decisions resulted in an updated rule-set for sheep and a new rule-set for grass:

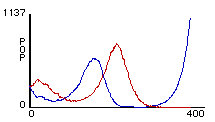
After selecting appropriate parameters and running her revised model, Talia found that her modifications had indeed brought about stable oscillations of size among the wolf and sheep populations. In addition, the level of grass in the model would oscillate as well. In examining plots of the population sizes over time, Talia noticed that changes in the sizes of the wolf population and in the level of grass would be roughly correlated, both varying as the approximate inverse of the number of sheep (figure 4).

Figure 4. A typical outcome from rule-sets W1+ S2 + P1. Red represents predator population size, blue represents prey population size, and green represents relative amount of grass.

In one sense Talia was surprised to find this model much more stable then the last, since she had given sheep more ways in which to die. Oddly enough, by limiting the resources of the sheep she had actually increased their chances of survival. On further reflection, Talia found this result known in the literature as the ‘paradox of enrichment’ (Rosenzweig, 1971) entirely reasonable. By not controlling the amount of food available to the prey, the prey population can grow without limit. This eventually causes the predator population to grow to unusually large levels, ultimately leading to a rapid and precipitous decimation of the prey. This effect is known to occur in the natural world just as it does in the StarLogoT world. Accordingly, those involved in wildlife conservation efforts now know that providing endangered species with an excess of resources may have the counterintuitive effect of decreasing their numbers.

A further surprise for Talia was that the introduction of grass an increase in the complexity of the model actually contributes to stability. This model, with its multiple fluctuating and interdependent populations, is more reminiscent of an ecosystem than the previous version. Contrary to engineering logic, this logic of this model suggests that complexity and noise in a system can result in stability, not only ‘chaos’. Modelers in biology, both amateur and professional, are sometimes quick to abstract biological phenomena from the environments in which they occur. This result, however, urges us that environmental and ecological context can play a significant role.

3.5 Spread out the Sheep

Talia’s revised model contains three species (wolves, sheep and grass), while she originally set out to build a model of predation between only two (wolves and sheep). She wondered whether she could find other rule-sets that would achieve the same effect as the grass, without including any additional species. She considered the role of grass in her revised model: it appears to assure that only a finite number of sheep can inhabit a given area. If there are too many sheep then the grass will run out and the sheep will starve, unless they move to another area that contains grass. Thus, she conjectured, the role of the grass is to limit the sheep population by placing a maximum density at which they can survive. Talia contemplated ways in which to impose such a density restriction on her model, without adding a third species. One simple way, she saw, would be eliminate the grass and instead to include a rule that explicitly restricts any patch from being occupied by more than one sheep:

Talia hypothesized that the resulting dynamics of rules W1 + S3 should look very similar to those of her three species model, only without the grass. In fact, when she actually ran the model she found its dynamics to be more similar to the first model she had built. The behavior was unstable, inevitably leading to the extinction of one or both of the two species. Something had gone wrong. Talia was now faced with various questions: Was her speculation on the role of grass in the previous model incorrect, or was there alternatively a problem in the way this speculation was tested? And if the speculation was indeed incorrect or incomplete, then what was the correct account? Talia realized that she would have to do more research.

We will not follow her inquiry, here, to its proper conclusion. Instead, we end our account while her research is still in progress. Further models will be designed, further accounts will be suggested, and, undoubtedly, further questions will arise in this process. Ultimately, we anticipate, the result of Talia's efforts will not just be a set of StarLogoT models, but, more importantly, an understanding of why they work in the ways they do.

3.5.1 Discussion: Answers versus theories

At one point in her investigation, Talia believed her third model (W1 + S3) had confirmed her hypothesis, and had actually produced dynamics qualitatively indistinguishable from those of her second model (W1 + S2 + G1). In this situation, how should she have chosen between these competing rule-sets? Which model should she have deemed correct? Talia’s answer was that one cannot choose between equally plausible rule-sets so long as they both yield equally plausible results. She came to see that her difficulty choosing was not specific to this example nor to StarLogoT modeling indeed, it is inherent in the process of scientific modeling. When multiple theories are equally compatible with existing knowledge, and neither theory is more predictive than the other (as in this scenario), then there will be no direct way to arbitrate between them (Quine, 1960).

Some teachers within the MSCP project were initially uncomfortable with this indeterminacy and sought to hide it from students. In our discussions with these teachers, we encouraged them to "dive into" the indeterminacy. Not only is such indeterminacy fundamental to scientific inquiry, but it may be valuable to students as part of their own thought processes. The modeling-oriented approach to learning biology shifts their goal from finding the correct theory, to finding a theory that is compatible with all the available evidence. The significance of this is that students need no longer search only for unique answers, which may be true or false in themselves, but spend also their time trying to compare theories against other theories. This shift of focus for the student from learning answers, to assessing theories for themselves is just the kind of high-level skill called for by educational policymakers and industry leaders at a time in which the turnover of scientific knowledge is so rapid (Chen, 199x; Murname & Levy, 1996). While content knowledge, or many of the "answers" in today’s textbooks are already out of date, the skill of assessing the validity and plausibility of answers is not so easily made obsolete.

Before we move on to the next example, it is worth noting that the methods and tools we have presented here are not only useful to students, but to professional scientists as well. The embodied approach, known to population biologists as Individual-Based Modeling, has become an accepted methodology within the field. Current individual-based models of predation are actually rather similar to the one we have developed in this section. In some cases, these models offer greater predictive accuracy than their classical counterparts (Huston 1988; Judson 1994).

4.0 Modeling Synchronized Fireflies

In the previous section, we showed how students can use StarLogoT as a tool to model and explore biological systems. In this section, we will elaborate on the ways in which students can, through the process of modeling, both learn about specific topics within biology, and use the StarLogoT modeling language as a laboratory for exploring biological mechanisms. Our example follows the inquiry of an undergraduate student, Paul, whose formal biology instruction consisted solely of high school biology courses. Through his involvement with the Making Sense of Complex Phenomena project, Paul learned of the phenomena of synchronously flashing fireflies and was intrigued. The following paragraph will provide some background.

For centuries, travelers along Thailand’s Chao Phraya River have returned with stories of the astonishing mangrove trees that line its banks. Come nightfall, these trees have been seen to flash brilliantly, on and off, intermittently illuminating the surrounding woods and the water below. A closer look at this display, though, reveals that the sources of these rhythmic flashes are not the trees at all. Rather, it the effect of thousands of individual fireflies inhabiting the trees, all pulsing their lights in unison. There are several species of firefly that are known to do this, such as the Southeast Asian Pteroptyx Malacae and Pteroptyx Cribellata. When one such firefly is isolated, it will typically emit flashes at regular intervals. When two or more such fireflies are placed together, they entrain to each other that is, they gradually converge upon the same rhythm, until the group is flashing in synchrony (Buck, 1988).

How do the fireflies achieve this coordinated behavior? When we think about how behavior is coordinated in our daily lives, we tend to think of schedules and elaborate plans. Paul was perplexed at how creatures that seem to have little capacity for such intelligent planning are nonetheless capable of such coordination. It was Paul’s suspicion that there must be a simple mechanism behind the feat of the synchronizing fireflies. His goal was to try to understand this mechanism by building a model of it in StarLogoT. Paul decided not to begin his inquiry by doing an extensive literature search. Instead, he was determined to see if, perhaps, he could find a solution on his own. He began his task with no more than the above description.

4.1 Approaching the problem initial assumptions

To begin, Paul made several working assumptions about these fireflies he was prepared to revise them later if necessary. First, he decided that the mechanism of coordination was almost certainly a distributed mechanism. That is, the fireflies were not all looking to a leader firefly for "flashing orders", but rather were achieving their coordination through passing and/or receiving messages from other fireflies. From his previous experience with StarLogoT, he had learned that not all coordinated group behavior requires a purposeful leader to direct the group (see Resnick, 1996; Wilensky & Resnick, 1999). Examples such as the food-seeking behavior of ants and the V-flocking of birds, implied that some forms of group organization could arise on their own. That is, as long as each organism follows a certain set of rules, then the whole group would be likely to organize itself. Paul’s seeking out of a distributed mechanism to explain firefly synchronization represents no small achievement.⁷ Elsewhere (Resnick & Wilensky, 1993; Wilensky & Resnick, 1995; Resnick, 1996; Wilensky & Resnick, 1999), we have described a "deterministic/centralized mindset" a tendency of most people to describe global patterns as being orchestrated by a leader giving deterministic orders to his/her followers. Paul’s experience in the MSCP project allowed him to overcome this tendency and consider leaderless non-deterministic mechanisms for firefly synchronization. Given the limited intelligence of individual fireflies, Paul surmised that just such a mechanism probably underlies firefly synchronization behavior. A second assumption, following the first, was that the system could be modeled with only one set of firefly rules; that is, with every firefly in the system following the same set of rules. Although he recognized that this assumption might have been too strong, just as ant and bee populations do divide roles among their groups, he decided to first try out the simpler hypothesis of undifferentiated fireflies. Yet a third assumption Paul made concerned the movement of the fireflies that it was not necessary to model this movement as coordinated or governed by deterministic rules, but rather it could be modeled as random flights and turns. From experience with other StarLogoT models, he had come to appreciate the role of randomness in enabling coordination (Wilensky, 1997; in press). In a wide variety of domains, ranging from the movements of particles in a gas, to the schooling of fish and the growth of plant roots, Paul had seen how stable organization could emerge from non-deterministic underlying rules. A final assumption was that the behavior of the fireflies could be modeled in two dimensions.⁸

4.2 Beginning with a simple model

These assumptions left Paul with the task of finding a plausible set of rules for a typical firefly. Rather than tackle this problem all at once, he decided it would be easier to begin with a simpler version. He started by modeling a flashing firefly that doesn’t synchronize. Paul contemplated how to represent a flash using a StarLogoT turtle. The solution came naturally: the turtle would change its color (say, to yellow) and then change it back. Now he needed a mechanism to regulate when the flash would occur. He knew that if left alone, a firefly would continue to emit flashes at a constant rate. Paul considered how to represent this simple behavior within his model firefly: this meant that every several clock-ticks, it should flash (change its color). In order for the flash to be seen, it would have to last at least one clock-tick. To accomplish this, Paul decided to give the model firefly a timer that would count down from a predefined reset-value (R) once the timer reached zero, the firefly would flash and reset the timer. In addition to the flash-timer, Paul also included a rule to cause the model firefly to "fly" around the screen. He assumed provisionally that a randomly generated flight path would be sufficient. He wrote the following rule-set:

After Paul debugged his StarLogoT code, his simple model worked. The fireflies would move around the screen and flash regularly, though of course they did not yet synchronize their patterns.

4.3 Thinking like a firefly

Paul was left to ponder what sort of additional rules might cause the fireflies to synchronize with each other. He considered the nature of coordination in general: could it ever be possible for distinct entities to coordinate their behaviors if they were unable to communicate with each other? No it seemed communication at some level would always be necessary for any coordinated behavior to occur consistently. He wondered what kind of communication mechanism might be used.

Often when building a model, students find it helpful to identify with the individuals within the model, and to view phenomenon from their perspective. At this point, Paul began to "think like a firefly". He reasoned along the following lines: If I were a firefly in that situation, what information would I have to go on? It would be dark, and I probably wouldn’t be able to see the other fireflies. I probably wouldn’t have much capacity for hearing or sensing the other fireflies either. I would, however, be able to see their flashes. Perhaps, then, I could look to see who else is flashing and then use this information to adjust my own flashing pattern.

4.4 Sorting through design options

Paul concluded that the flashes themselves could serve to communicate the necessary information, and he wanted to make this possibility more concrete within the context of the StarLogoT environment. He had already decided that in order to flash, a firefly changes its color from black to yellow, and back to black again. A firefly must, then, be searching for other yellow fireflies. There are many ways that such a search might be carried out in StarLogoT, and Paul found that he had some choices to make. The process of formalizing his model forced Paul to confront questions that he hadn’t already considered: How many other fireflies should a firefly look at? At what distance could it detect a flash? How many flashes should it be allowed to take into account?

Paul saw that there didn’t have to be any strictly correct answers to these questions, since they were, questions about simulated fireflies not actual fireflies. For example, it would make little sense to ask how many patches away actual fireflies can see! Still, Paul thought that at least the issue of whether a model firefly should survey the flashes of all or only a part of the population should have a clear answer. For it would be possible to allow a model firefly to detect all flashes in the population at a given clock-tick, but this would surely be granting the firefly too much information; model fireflies shouldn’t be much more intelligent or perceptive than real ones. Since a real firefly would only be able to perceive a subset of the flashes in the population, Paul decided that the model firefly should scan only adjacent patches in order to look for yellow fireflies. He began with a rule that allows a firefly to sense other flashes within a radius of one patch. This decision only partly simplified the question of what a firefly senses. Consider some statistics that a firefly might collect about observed flashes: overall brightness (i.e. the combined light of all observed flashes) during a given clock-tick, the number of distinct flashes observed during a clock-tick, the number of clock-ticks between observed flashes, increases in relative brightness from clock-tick to clock-tick, simply whether or not any flash had been observed at all at a given clock-tick, etc. At this time, Paul did not have any principled way of choosing amongst these data collecting options, so he decided to proceed without committing to any of them.

Given that a firefly has some mechanism for perceiving flashes, and perhaps for analyzing this information in some way, the next question that Paul faced was what to do with this information. In what way would a firefly alter its flashing behavior in response to whatever had been observed? Paul tried to think of a simple situation in order to make sense of the problem. Once again, he took the perspective of a firefly: Suppose I perceive a clear pattern among the other fireflies for example, everyone else is already synchronized. Then, as long as we all have timers of the same duration, it would be simple to match this pattern. Upon seeing everyone flash, I would reset my timer as if I had flashed as well. Then my next flash would coincide with everyone else’s.

Having understood what to do at one extreme, Paul tried to work backwards: At some point, before everyone else is synchronized, I must be confronted by a multitude of unsynchronized flashes. Then what would I look at? To what would I reset my timer? Paul thought again of all the different ways that a firefly might analyze observed flashes, and all the different timer-reset rules that must be possible. Paul had many ideas, but he felt that he needed more information to continue.

4.5 Researching the relevant biological literature

Notice how far Paul was able to get without reference to detailed information about the real-world phenomenon. From his initial goal to model ‘whatever’ was going on, he was able to reason to this point where he was seeking a very particular sort of algorithm. It might have been possible for someone to take this line further, but in order to decide among some of the options he had left open, Paul felt a need to gather information about the behavior of real fireflies. For example: does the interval between successive flashes vary from firefly to firefly, how far can an actual firefly see, how many flashes can it take into account, what is the timer-reset rule.

At this point, Paul did some research into the scientific literature. His own investigation had not answered all his questions, but it had given him a sound context from which to understand and interpret the existing research. In looking through the literature he was not reading a teacher’s assigned material, but rather engaging in his own research to answer questions of his own devising. Paul located several journal articles in order to help answer his questions. He found out the following (Buck, 1988; Buck & Buck, 1968; Buck & Buck, 1976; Carlson, 1985):

• Fireflies do indeed have internal ‘timers’ to regulate the period of flashing, and are known to entrain their timers to observed rhythms.
• The only information needed for entrainment is that of other flashes.
• There are many species of synchronizing fireflies, all with different entrainment and oscillation characteristics.
• Some species are able to adjust the period of oscillation, others are not. For the latter, the period of oscillation tends to remain highly constant across a population.
• Different methods of synchronization are seen across species. Two main mechanisms are phase delay and phase advance synchronization:
  • Phase-delay: when a firefly perceives any flash, it delays its next flash so that it will occur one period after perceived flash. This is the strategy known to be employed by the Southeast Asian fireflies of the Pteroptyx genus.
  • Phase-advance: when a firefly perceives any flash during a short window of time before flashing, it flashes immediately and starts a new period immediately thereafter. This strategy is known to be used among species that tend to synchronize only rarely and transiently, such as the American Photinus Pyralis.

Paul was pleased to discover that many of his design decisions were biologically plausible, such as his focus on a distributed synchronization mechanism, his use of timers to control flashing, and his decision to allow timers of the same duration across the population. The synchronization mechanism he had thought of earlier appeared to correspond to the phase-delay mechanism from the text, although he was surprised to learn that a firefly needs to see only one flash, any flash, in order to react. His next step was to extend his existing model in order to determine whether this would really work.

4.6 Modeling phase-delay synchronization

Paul decided to model the phase-delay mechanism first. The research did not turn up any information on the maximum distance within with a firefly can perceive other flashes, and so Paul had to decide on this matter on his own. For representational simplicity, he chose to allow fireflies to sense other fireflies within a radius of one patch. Incorporating his earlier model, this resulting in the following rule-set:

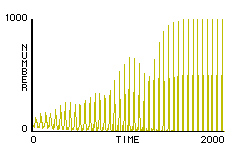
Paul ran rule-set F2 using 1000 fireflies, and was amazed to see the model fireflies converge upon a single rhythm before his eyes. He also set up a plot to display the number of fireflies flashing at a given time (figure 5).

Figure 5. Typical plot of the number of flashes in a population at a given time under rule-set F2.

4.7 Modeling phase-advance synchronization

Next, Paul wanted to try out the phase-advance strategy. This required more sophistication, since a phase-advance firefly will only adjust its timer during a short window before its flash. Paul amended F2 to account for this:

Indeed, Paul found that this strategy was not as effective as phase-delay synchronization when he ran this rule-set (figure 6), he did not observe synchronization at all! It was only after much experimenting that he discovered a variant of this rule-set (see F4 below) that did produce synchrony, although the synchrony took much longer to develop and was not as precise as with rule-set F2 (figure 7). Rather than flash in perfect unison, the fireflies would all flash within an interval of two or three clock-ticks.

While he had managed to achieve synchronization using a phase-advance mechanism, Paul was uncomfortable with this result since he had done this by means of an ad hoc change to his model. He wondered whether, perhaps, this result predicted the behavior of actual fireflies, or whether it was a just an artifact of the representational decisions he had made.

Paul tried a number of further variants to rule-set F4 to investigate other possible flash-reset mechanisms. Among them was one where he omitted the requirement for a flash-window (W). He quickly discovered why this window was necessary: without it, the fireflies would persistently reset each other’s timers, and there would be no interval between flashes.

4.8 Further questions for research

Paul was encouraged by the initial results of his research and was left with new questions to investigate. For example, he was intrigued by the ability of some fireflies to adapt not only the timing of their flash, but also the duration between flashes. The papers he had looked at gave no complete theory of how this could be done. He was also interested in customizing his model to reflect the idiosyncrasies (e.g. multiple consecutive flashes, responses to irregular stimuli) of particular species, such as Pteropox Malacae and Photinus Pyralis. Though he began his inquiry with only a single question in mind, he found that his questions multiplied as his research continued.

4.9 Discussion: the model testing process

What makes a model a scientific model is that it has been tested against whatever system it was designed to represent. At this point, Paul’s phase-delay model was successful in having the model fireflies collectively synchronize their flashing patterns, but the correspondence between this model and reality still needed to be tested. Indeed, Paul went through such a process of testing, and eventually was convinced of the soundness of his modeling decisions. In this section we will remark upon his experience in order to frame a discussion about the process of testing and evaluating StarLogoT models in general.

Why bother testing at all? In one sense we know that Paul's model works, for the model fireflies do indeed synchronize. However, we have already discussed the dangers of models that bear only a superficial correspondence to the phenomena being modeled, and here there is certainly a danger. Perhaps there are many different algorithms that will lead to synchronization. How do we know that Paul’s model corresponds in a meaningful way to the behavior of real fireflies? We have some indication, since journal articles have confirmed many of Paul’s assumptions. Still, Paul may have made errors in coding his model, he may have misinterpreted the literature, and, of course, the literature itself may have been incorrect. Ideally then, we would like more evidence that the model is sound. In order to evaluate a model, a modeler must critically analyze the content and output of the model along several dimensions. These include the soundness of the model’s underlying assumptions, the robustness of its output, and its predictive capacity. Let us consider each of these in turn with respect to Paul’s model.

Continually evaluating the plausibility of the background assumptions is a modeler’s first line of defense against specious models. Whenever design decisions are made, the modeler should be aware of the ways in which these decisions may detract from the realism of the model. He/She may then make a deliberate choice to stay with these decisions, reject them, or, perhaps, to wait until later to choose. For example, when Paul decided that all fireflies would follow the same rules or that the relevant behavior could be adequately modeled in two dimensions, he made these decisions provisionally. He was aware of the conceptual jump he had made, and was prepared to retract these assumptions if necessary. Any model will take representational liberties. The important thing is to be aware of these, and to try and discern whether and how they affect the plausibility of the model.

Another way to evaluate a model is to consider its ‘robustness’. A robust model will yield consistent results, even when we introduce noise, adjust the parameters, or even effect small changes to the background assumptions. If we do obtain consistent results under these conditions, we have evidence that our model is not overly sensitive to our assumptions or chosen parameters some of which may be arbitrary or mistaken. We may reasonably suspect a non-robust model of being implausibly contrived, or curve-fitted (see section 3.4.1). It was on these grounds that Paul had been suspicious of his phase-advance model. He wanted to further test his phase-delay model along the same line. Paul figured that a robust solution to the synchronization problem should be able to hold up under non-ideal, or ‘noisy’, conditions, where other factors might interfere with the phase-delay algorithm. One way that he tested his solution was to introduce several "blind" fireflies that would not synchronize with the rest, but would still flash. When he tried this, he found that the population took much longer to settle into a stable pattern of synchronization. In the meantime, only small clusters of synchronization would transiently form and then break up again within the population (figure 8). Paul was pleased to find that the algorithm held up under this condition, and that this local clustering had even been observed in natural Pteroptyx populations (Buck, 1988).

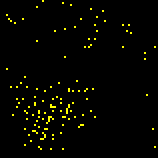
Figure 8. Clusters of synchronization within a population of 1000 fireflies.

Of course, the principal way that scientific models are evaluated is by determining how well they can be used for prediction. By this, we mean that the model anticipates some result that is approximately true of the system being modeled, and that did not itself factor into the development of the model. New data against which to compare a model might be collected in the laboratory or from nature, though research in journals and other texts will often provide enough data for the purposes of students. The predictions that student models may offer for this data are typically of a qualitative rather than quantitative nature. In Paul’s case, for example, there was the unexpected result from the "noisy" fireflies. His later discovery that this is actually in accord with real firefly behavior constitutes an item of predictive evidence in favor of his model. Ideally, a student would attempt to find and amass as much such evidence as possible.

Testing can take place after students have developed their initial models, or, often, it will be concurrent with the process of development. All along, students always have the options of either concluding the modeling process, or going back and revising their models in light of what they have discovered. In the end, even after students have critically evaluated their models, they must (once again) confront the inevitable indeterminacy that surrounds the testing of scientific theories. Theories are never conclusively proved (Popper, 1959). Accordingly, students should not walk away from the modeling process believing to have found the correct solution. Rather, they should leave with an awareness of the ways that their model both does and does not reflect the system they set out to capture.

Critical thinking about modeling does not come easily to many students. In the Making Sense of Complex Phenomena project, we have observed that for many students StarLogoT modeling is their first experience where such thinking the sort that underlies experimental science is demanded. We have found that students engaged in StarLogoT modeling, through revising, assessing and successively refining their models do, indeed, develop a propensity for critically evaluating their models. This propensity, however, is hard won. Typically, it is only after a good deal of guidance that students will become critical of the representational decisions they have made. Further research is needed on how to help students to move beyond good model building to good model critique. In our concluding remarks, we will argue that significant learning occurs even when students do relax the requirement of criticality.

4.10 Further Reflections: Learning through Building

Let us call this the engineer’s dictum: if you can’t build it then you don’t understand it. Our approach of modeling underlying mechanisms takes the engineer’s dictum seriously. In order to model a system, it is not sufficient to understand only a handful of isolated facts about it. Rather, one must understand many facts and concepts about the system and, most importantly, how these relate to each other. The process of modeling is inherently about developing such conceptual relations, and seeking out new facts and concepts when a gap in one’s knowledge is discovered.

We have seen how Paul came, through building, to understand the concept of a simple circuit capable of entrainment. In science and mathematics, such circuits are known as oscillators, and networks of such circuits are known as coupled-oscillators. As it turns out, such oscillators do not only underlie firefly synchronization, but a wide-range of phenomena throughout biology that exhibit synchronization behavior without any centralized control. Among other phenomena, oscillators are involved in acoustic synchronization between crickets, the pacemaker cells of the heart, neural networks responsible for circadian rhythms, insulin secreting cells of the pancreas, and groups of women whose menstrual periods become mutually synchronized (Mirollo & Strogatz, 1990). Though Paul’s goal was to learn about fireflies, he had come to understand a concept that has applications far beyond.

5.0 Concluding Remarks

¹ For a similar and much fuller account of the gap between school and research physics, see (Hammer, 1994).

² For a detailed discussion on misconceptions reconceived, see (Smith, diSessa & Roschelle, 1996)

³ For an illuminating discussion of this transformation of the biological field, see (Allen, 1975)

⁴ The predator-prey model and numerous other models (collectively known as "Connected Models" (Wilensky, 1998)) can be downloaded from "/cm/models".

⁵ For some recent predation models, as well as some other classical biological models see (Murray, 1998).

⁶ The rule-sets are stated in summary form here. For the actual StarLogoT code, please visit /cm/models.

⁷ It is interesting to note that some of the first theories proposed to explain synchronously flashing fireflies were, in fact, "leader" theories (Morse, 1916; Hudson, 1918).

⁸ While the first three assumptions were derived, to a great extent, from Paul's understanding of plausible biological mechanisms, this last assumption was primarily driven by the limitations of computer displays and of the StarLogoT language itself. Since building a three-dimensional model is more difficult in StarLogoT, Paul was, essentially, hoping that the three dimensionality of the firefly world was the not the key factor in enabling their coordination.

Acknowledgments

The preparation of this paper was supported by the National Science Foundation (Grants RED-9552950, REC-9632612), The ideas expressed here do not necessarily reflect the positions of the supporting agency. Rob Froemke played a significant role in the development of the StarLogoT modeling environment with the assistance of Eamon Mckenzie, Paul Deeds and Dan Cozza. Mitchel Resnick, Brian Silverman and Andy Begel were largely responsible for a previous StarLogo version, StarLogo 2.0, on which StarLogoT was based. Steve Longenecker and Josh Mitteldorf contributed greatly to our thinking about the predator-prey models. Ed Hazzard, Walter Stroup and Rob Froemke made valuable clarifying suggestions. We would like to thank Seymour Papert for his overall support and inspiration and for his constructive criticism of this research in its early stages. Mitchel Resnick has been an invaluable collaborator in thinking about issues of complexity and education in general and in exploring the predator prey models in particular. Daniel Dennett provided valuable criticism of the firefly model and inspired many of our observations about embodied modeling.

References