GasLab - an Extensible Modeling Toolkit for Exploring Statistical Mechanics

Uri Wilensky
Edmund Hazzard
Robert Froemke

Center for Connected Learning and Computer-based Modeling
Northwestern University
Annenberg Hall 311, 2120 Campus Drive
Evanston, IL 60208, USA
uriw@media.mit.edu

Proceedings of the Seventh Annual European Logo Conference EUROLOGO 99, Sofia, Bulgaria

Abstract

GasLab is a collection of connected StarLogoT models of the behavior of gas molecules in a box. The GasLab project was designed to help students to visualize the physical behavior of an ideal gas and relate the idealized microscopic molecular rules to the measurable observable quantities that emerge. GasLab is an extensible modeling toolkit — a domain-rich set of models that is embedded in the general purpose modeling language StarLogoT. By exploring the GasLab models and then using StarLogoT primitives to extend the models in the direction of student inquiry, students are able to do sustained scientific investigations. In this paper, three such investigations are described. GasLab provides school-age children with access to the powerful ideas of statistical thermal physics.

1.0 Introduction

The latest version of StarlogoT and an associated collection of "extensible" models (collectively entitled "Connected Models") are available for download at ccl.northwestern.edu/cm. The models are drawn from a wide range of disciplines including physics, biology, mathematics, computer science, chemistry, materials science, ecology and economics.

When used in the classroom, the pedagogy used in the MSCP Project has four basic stages¹. a) In the first stage, the teacher presents a "seed" model (a simple starting model) to the whole class, projected through an LCD panel so that everyone can view it. The teacher engages the class in discussion as to what is going on. Why are they observing that particular behavior? How would it be different if model parameters were changed? Is this a good model of the phenomenon it is meant to simulate? b) In the second stage, students run the model (either singly or in small groups) on individual computers and explore the parameter space of the model. c) In the third stage, each modeler (or group) proposes an extension to the model and implements that extension in the StarLogoT language. Modelers starting with GasLab, for example, might try to add to the model by building a pressure gauge, a piston, a gravity mechanism, or heating/cooling plates. The extended models are added to the project’s library of extensible models and made available for others to work with as "seed" models. d) In the final stage, students are asked to propose a phenomenon and build a model of it from "scratch" using the StarLogoT modeling primitives.

We have worked with and observed classrooms in all four of these stages. Generally, the depth of understanding of complex systems and emergent phenomena would be expected to increase as the student more actively builds, modifies, and explores with the model. The results that students can achieve with model extensions and designing their own models are often quite dramatic. Because of the great variations in available technology, learning time, and classroom organization, each stage has valuable applications.

This extensible modeling approach allows learners to dive right into the model content. Learners typically start by exploring the model at the level of domain content. When they are puzzled by an outcome of the model, they design an extension to the basic model. This extension usually requires only a few language primitives to implement. This allows learners to follow a gently sloping path towards full StarLogoT language mastery — skill with the general purpose modeling language is acquired gradually as learners seek to explain their experiments and extend the capabilities of the model.

2.0 GasLab — an extensible model

Statistical mechanics — the behavior of large numbers of molecules each following individual rules of motion — and the related discipline of thermodynamics — the study of heat — is a classic example of an effort to understand complex behavior that emerges from a relatively simple set of local rules. It plays a fundamental role in physics. It is also one of the harder subjects for students at all levels to understand. A number of reasons for this difficulty are suggested from an examination of the literatures of science & mathematics education and cognitive psychology.

• There is an abundance of cognitive science literature demonstrating the difficulty of probabilistic/statistical thinking for most people, in a wide range of subjects (e.g., Konold, 1991; Phillips, 1988; Piaget, 1951; Tversky & Kahneman, 1974, Wilensky, 1997), and statistical mechanics rests on this kind of thinking.

• A formal corpus of mathematics was developed in the nineteenth century to handle many-body problems because other means, such as high-speed reiterative calculators, were not available. This set of formalisms serves as a barrier, a filter that allows only those with advanced mathematical training to access the powerful conceptions of statistical mechanics.

• Although heat is identical with molecular motion, thermodynamics as a theoretical system is abstracted from the underlying phenomena, making it hard to grasp the physical meaning of thermodynamical principles.

Thus the rules of heat transfer, heat engines, phase changes and entropy may be easy to state, but a deeper understanding of how these rules arise and their web of meanings eludes most students.

The GasLab project was designed to help students to visualize the physical behavior of an ideal gas and relate the idealized microscopic molecular rules to the measurable observable quantities that emerge. GasLab is a suite of connected StarLogoT models of the behavior of gas molecules in a box². Particles, color-coded by speed, are modeled as billiard balls colliding elastically with the walls of the box and with each other. Feedback to the user is visual and immediate as a display of the changed states of individual particles. A graphical user interface includes command buttons, sliders for initial conditions, and monitors to keep track of numerical variables. General-purpose plotting primitives allow traditional real-time plots that show summary statistics, such as average speed, energy, and histograms of speed distribution of the molecules.

Traditional high school science instruction segregates the study of the micro-level phenomena, such as colliding molecules (in Newtonian mechanics), from macro-level phenomena, such as the gas laws (in chemistry). The connection between these two levels is passed over. But it is in the connection that the explanatory power of physics resides; the kinetic theory of gases infers the gas laws from a model of molecular behavior. By providing an environment in which these connections are easily made, school-age children are given access to the powerful ideas of statistical thermal physics, even though they are not facile in the complex mathematics that goes with it.

GasLab is both a physics simulation and an environment for visualizing and strengthening intuitions about the statistical properties of ensembles of interacting elements. Students can get a feel for both the macro-level behavior of the ensemble in the aggregate and its connections to what is happening at the level of the individual gas molecule and the rules it follows. Through programming the molecules and surroundings with whatever properties are desired, learners can design experiments in GasLab and then "run" them and view the results. Because GasLab is embedded in a general-purpose modeling language, many subtle experiments can be run by users, according to their interest, including some which are difficult or impossible to do with real gases (e.g. Maxwell’s Demon, see below).

3.0 Examples: Introduction

The GasLab environment was designed to allow students to extend the basic model in whatever direction their interest carries them. Both students and researchers working with GasLab have developed a wide range of model extensions, such as: the relationship between pressure, temperature and volume; the diffusion of two gases; the effects of gravity on an atmosphere; Brownian motion and the measurement of mean free path; how a piston does work on a gas; and thermodynamic paradoxes such as Maxwell’s Demon. Each of these models was then distributed and could in turn be modified and extended by other users to further investigate the questions that the model raised.

In this section of the paper, we describe three examples of students posing questions to the basic GasLab model and devising extensions that allow them to pursue their questions "experimentally." The examples presented here have arisen across multiple contexts. They were developed by high school students in traditional classroom instruction, by high school students in after-school settings, by college students both as part of class projects and as part of free exploratory activity, and by high school teachers, both in-service and pre-service. The GasLab suite grew as all these people explored, extended, revised and created new models. Members of our research team were in charge of consolidating these many versions and innovations and creating a robust suite for wider distribution. As such, the research team also engaged in revision and extension of GasLab models, and we too significantly enriched our understandings of this branch of physics. For clarity of exposition, we will describe each of our three examples as single stories, though in actuality these stories are composites of modeling experience by students, teachers, researchers and developers throughout the MSCP Project.

In the concluding section, we analyze some of our observations of rich learning using GasLab and discuss some of the features of GasLab that make it a powerful tool for studying thermodynamics and statistical mechanics.

3.1 Molecular Speed Distribution

One of the immediate insights afforded by this model, as previously reported (see Wilensky, in press), is what happens to the speed distribution of molecules free to collide elastically a large number of times. Several output displays provide relevant information: a) the graphics window which shows the moving molecules and a tracing of one molecule’s path (Fig.1); b) a dynamic plot of the number of slow, medium, and fast molecules (Fig.2); and c) a speed histogram (Fig.3).

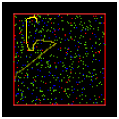Fig.1: Graphics Window

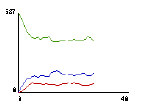Fig.2: Speed Counts

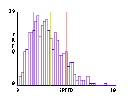Fig.3: Speed Histogram

When students first observe this model, they are usually surprised and puzzled by several features: a) the average energy of the molecules remains constant, but the average speed decreases; b) there are more slower-than-average molecules than faster-than-average ones. In the ensuing discussion, the following related ideas emerge: a) energy is proportional to the square of the speed, so the sum of the squares of speeds is constant, but the sum of speeds is not. Total energy remains constant, but total speed does not. b) Several slow molecules are needed to balance a single fast one (e.g., 4 squared is greater than 2 squared plus 2 squared). c) The emergent Maxwell-Boltzmann speed distribution looks a lot like a Gaussian bell-shaped curve, but it’s asymmetrical because there’s a minimum value speed (zero) but no maximum, and the high speeds "cost" more in terms of energy.

For most students, witnessing this emergence of the Maxwell-Bolzmann distribution from the underlying molecular interactions is an entirely satisfactory explanation. Some students raise further questions. Why this particular shape to the speed distribution? Would this shape show up in other situations, too? If the collision rules were slightly different, would this distribution still look the same?

To explore his, we can create a simple StarlogoT model in which two molecules exchange "goods" whenever they meet. Instead of following complex collision rules, each exchange keeps a simple sum constant — sum of goods, or sum of squares of goods. Thus a single aspect of the model can be isolated. The histograms of each exchange rule are as follows:

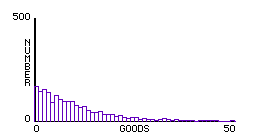Fig.4: Constant Sum of Goods

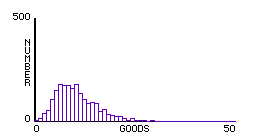Fig.5: Constant Sum of Squares of Goods

In this way, we can demonstrate experimentally that any exchange in which the sum of the squares of goods is constant — as is the case when 1/2 mv² is conserved — gives a similar distribution. Maxwell’s concluding remark in his original derivation of the distribution parallels this result:

It appears from this proposition that the velocities are distributed among the particles according to the same law as the errors are distributed among the observations in the theory of the "method of least squares." The velocities range from 0 to infinity, but the number of those having great velocities is comparatively small. (Maxwell, 1860)

At this point, a larger mathematical principle has emerged from a molecular model. Many students working in GasLab noticed this connection. In economics, this phenomenon is called Paredo’s Law, whereas a limited resource comes to be distributed unevenly in a population: many members of the population possessing very little, some possessing a moderate amount, and a very few possessing a great deal of the resource.

Many students are intrigued by yet another fundamental question: how do molecules of equal mass and speed gradually develop unequal speeds? At first glance, it might seem that since two equal masses simply exchange their speeds when they collide, what’s equal to start with ought to stay that way.

Students devise many approaches to resolve this problem. One is a simple StarLogoT model that examines a single collision in isolation. By watching many different single collisions (see below), students understand, intuitively (as well as through the formulas of mechanics), how a moving center of mass in a collision can give rise to unequal velocities.

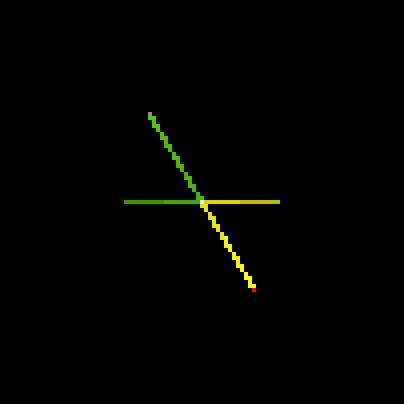Fig.6: Head-on Collision, Center of Mass Fixed

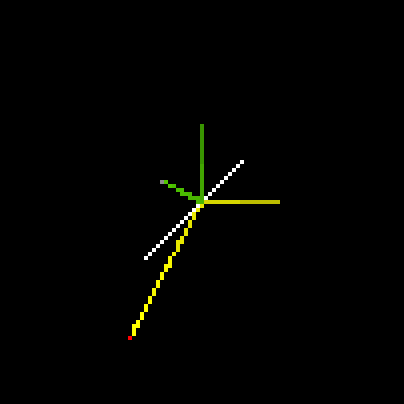Fig.7: Collision at 90deg., Center of Mass in White

Some students pursue their investigation by examining, very carefully, the "billiard-ball" collision model upon which GasLab was built, which in turn was based on Maxwell’s original derivation (Maxwell, 1860). In the process of looking more carefully at the collisions, one can track the random path that an individual molecule follows (Fig.8). This path looks very much like Brownian movement, the name given to the random motion observed in microscopic particles suspended in a fluid (Fig.9). Students then explore analytically the average time and distance between collisions and see how this is related to rates of diffusion.

Fig.8: Paths of Molecules in GasLab

Fig.9: Paths of Microscopic Rubber Particles3

3.2 Molecules with a plunger

A simple gas-filled piston is a classic conceptual tool for the study of thermodynamics. Many thought experiments use it to explore the relationships among pressure, volume, and temperature as heat and mechanical energy are added or removed. Heat engines and refrigerators are analyzed in this way by breaking the cycles down into several simpler steps — usually one of the three variables is held constant for clarity of analysis. Now that we have a functioning model of an ideal gas, a two-dimensional simulation of an insulated piston is a natural next step that was taken by many users of GasLab.

One version of this exploration is a box with a plunger that simply changes the "volume"⁴ of the box but doesn’t interact with the molecules. When the plunger descends, the molecules are moved downward without changing their speed. Pressure varies inversely with volume, and energy remains the same. The visual feedback from the GasLab model leads students to posit an account of this macro-level phenomena in terms of molecular movement: pressure is caused by the molecules bouncing off the walls and transferring momentum; and as the density of the gas goes up, more molecules hit the walls, so there’s more pressure.

Fig.10: Starting Position

Fig.11: Plunger Up

Fig.12: Plunger Down

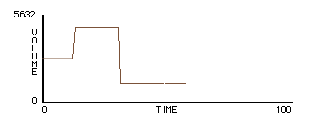Fig.13: Volume vs. Time

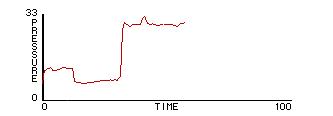Fig.14: Pressure vs. Time

This model raises a puzzle. It is "isothermal", because the energy, and hence the temperature, of the molecules doesn’t change. We know about bicycle pumps: you can heat up a gas by compressing it. How does a real plunger impart energy to the gas? "It does work" isn’t a sufficient answer. One needs to understand the actual mechanism, at a microscopic level, in order to extend the model. In the process of designing a mechanism for the plunger, students come to model a molecule bouncing off the plunger as the same type of two-body collision as between molecules, except that one mass (the plunger) is very large and slow compared to the other. The plunger imparts additional momentum to the molecules as it descends and removes momentum as it rises.

Based on this notion, some students write an "adiabatic piston" model, where no heat energy is lost — only mechanical energy to and from the plunger. The plunger is given "weight" — acceleration due to gravity — by adding to its downward speed a little bit at each clock tick⁵. It is then natural to predict that, at some given set of parameter values, the upward pressure caused by molecules striking the plunger will balance the downward acceleration of the plunger.

By experimenting with parameter values for masses and speeds, an equilibrium point for the plunger is found. The plots of plunger position, energy, and pressure reveals a gently oscillating system in which all three variables — pressure, volume, and energy — are changing simultaneously.

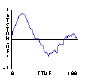Fig.15: Piston Speed

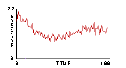Fig.16: Pressure

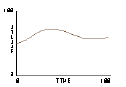Fig.17: Volume

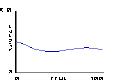Fig.18: Energy

3.3 Molecules under gravity

Once we have a working model of an ideal gas, we can ask whether it would behave like an "atmosphere" if a gravitational force were imposed on it. This is equivalent to giving each molecule a slight increase in downward velocity at each clock tick⁶. Students who performed this simple modification generated an atmospheric model (see below) which can help build an intuitive foundation for a number of phenomena:

• Each molecule follows the law of gravity and moves in a parabolic trajectory, however briefly, like a thrown ball (note traced path in yellow).

• The gas becomes denser near the earth (bottom of screen) and the net effect is a decreasing density as height increases.

• Some fast-moving molecules can escape altogether, if gravity is weak.

• The atmosphere gets "hot" as it collapses toward the earth — an example of gravitational potential being converted into heat. This is a very important phenomenon in stars.

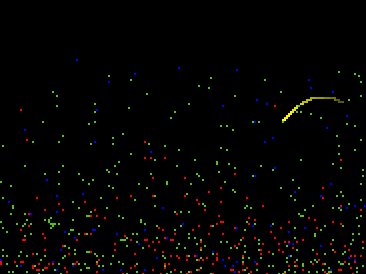Fig.19: Graphics Window (one molecule traced)

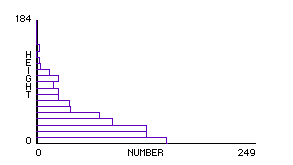Fig.20: Density vs. Height

These insights, while relatively easy to observe in the GasLab-atmosphere model, are not obvious, even to professional scientists. In a discussion of the atmosphere model with two visiting biologists, they affirmed that the atmosphere was held to the earth by gravity, but when asked why all the air wasn’t pulled right down to the ground, they were at a loss. We would like to suggest that the picture of molecular motion afforded by GasLab, where the equilibrium between gravity and pressure is visually vivid, along with the ability to test out their theories, would have given them a concrete framework for making sense of the dynamic stability of the atmosphere (see Wilensky, 1991, in press).

4.0 Discussion

4.1 Learning physics with the aid of GasLab

Certain features of StarLogoT proved especially helpful for students in overcoming some of the difficulties in understanding thermodynamics and statistical mechanics. The fact that the molecular model and the collective behavior of the gas could be visualized at the same time greatly enhanced students’ grasp of the physical situation and hence the quality of their explanatory thinking. It also enabled them to make a clear link between the mechanistic behavior of individual molecules, on one hand, and the aggregate averages which have probabilistic meaning, on the other. The ability of students to easily move across two levels of phenomena greatly aided hypothesis generation and explanatory power. (Wilensky & Resnick, 1999) In addition, the availability of simultaneous multiple active representations, in the form of moving molecules (the graphics window), individual turtle monitors, real-time plots of macroscopic values, and distribution histograms, gave students many ways to explore the phenomena without resorting to the complex derivations and mathematics of statistical mechanics. One student expressed how much more meaningful it was to watch a graph develop over time than to just see it after the fact.

4.2 Similarities to experimental science

How does experimenting with a simulation of this kind compare with experimental science in the laboratory, with respect to how students are learning to think about science? This is especially significant because real lab work is difficult to carry out in classroom settings. Teachers often rely on "cookbook" or demonstration experiments. Little time is given to exploring alternative theories with colleagues, devising and carrying out one's own ways to test a given explanation, or wrestling through all of the complexities of gathering good experimental data.

Students working with GasLab demonstrated patterns of thinking and activity surprisingly similar to those of scientists doing experimental science. The mapping between the two is by no means exact. Nonetheless, there are a significant number of common patterns of thinking, all of which were observed during the development of GasLab:

• One revisits and builds on previous experiments by others.

• There is a continuous iterative loop between theory and experiment, each refining the other.

• There are many test runs before the "final" most refined version of the experiment.

• One moves from qualitative observation to quantitative measurement, as the phenomenon becomes clearer.

• One varies parameter values to test and extend a theory — "if the volume goes up, the pressure should fall".

• Only repeatable phenomena are credible.

• Every experiment suggests many others, to answer new questions and extend one’s confidence in the theory.

• Difficulty in getting the expected results can arise from many sources. There could be faults in the measuring apparatus or how it is used, a mathematical mistake, a "bug" in the code", an inaccurate mental model, a conceptual error in the theory, or a problem in the chain of reasoning that followed from it. One may well be led back to the fundamental assumptions of the theory. Sorting out what’s "wrong" and how to be sure of it is a big part of doing experiments, and it requires great mental agility and imagination. This sort of exploration is readily possible in StarLogoT, and it led to many extensions of the GasLab models.

Results can be surprising — in StarLogoT because the emergent patterns of complex systems are often counter-intuitive, and in nature because our theories are always partial sketches of a complex reality.

GasLab modeling presents some unusual additional opportunities, such as the ability to reproduce classic experiments by simulation (e.g. the free expansion of a gas into a vacuum), or to model famous thought experiments, such as Maxwell’s demon, a tiny being who could separate hot from cold molecules, thus violating the 2^nd Law of Thermodynamics (Maxwell, 1871).

In summary, GasLab is a domain-rich modeling suite embedded in a general purpose modeling language. The combination of these two features presents opportunities for investigation and learning that are lacking in traditional laboratory instruction. Teachers can plan complex thought experiments, including some that can’t be observed in natural settings (e.g. studying the path of single molecule); and the rapidity with which new variations can be tried greatly facilitates discussion. GasLab facilitates a lively, inventive, problem-solving style by users that more nearly matches actual scientific practice than do traditional school lab activities.

4.3 Rich discussions

The preparation of this paper was supported by the National Science Foundation (Grants RED-9552950, REC-9632612), The ideas expressed here do not necessarily reflect the positions of the supporting agency. We would like to thank Seymour Papert for his overall support and inspiration. Mitchel Resnick gave extensive support in conducting the original GasLab research and has been an invaluable collaborator throughout. Wally Feurzeig, Nora Sabelli, Ron Thornton and Paul Horwitz made valuable suggestions to the project design. Paul Deeds, Ken Reisman and Daniel Cozza contributed to the design and implementation of several GasLab models. Josh Mitteldorf has been an insightful critic of the subtle points of thermodynamics. Walter Stroup has been a frequent and an invaluable collaborator throughout the GasLab project.

References

¹The word "stage" can be somewhat misleading as some classrooms start at the "final" stage and others do only the first stage. Many classrooms do, however, follow this progression of pedagogical settings.

²The GasLab Toolkit originated with a model called GPCEE, which was later called Gas-in-a-Box. GPCEE was originally developed as part of the Connected Mathematics Project (Wilensky, 1995).

³Halliday & Resnick, 1962

⁴The GasLab models are two dimensional. In most cases, two dimensional gas models behave similarly to three dimensional ones. In the cases in which they diverge, GasLab will yield inaccurate results. While it is reasonably straightforward to create three dimensional GasLab models in StarlogoT, the visual complexity of the models is not as conducive to learning.

⁵A clock tick, the model's unit of "time", is equal to one iteration.

⁶Ignoring the curvature of the earth.