
|

|

|
GasLab -- an Extensible Modeling Toolkit for Connecting Micro- and Macro- properties of Gases
Uri Wilensky
Center for Connected Learning and Computer-Based Modeling
Northwestern University

|

|

|
1.0 Introduction: Dynamic Systems Modeling
Computer-based modeling tools have largely grown out of the need to describe, analyze and display the behavior of dynamic systems. During recent decades, there has been a recognition of the importance of understanding the behavior of dynamic systems—how systems of many interacting elements change and evolve over time and how global phenomena can arise from local interactions of these elements. New research projects on chaos, self-organization, adaptive systems, nonlinear dynamics, and artificial life are all part of this growing interest in systems dynamics. The interest has spread from the scientific community to popular culture, with the publication of general-interest books about research into dynamic systems (e.g., Gleick 1987; Waldrop 1992; Gell-Mann 1994; Kelly 1994; Roetzheim 1994; Holland 1995; Kauffman 1995).
Research into dynamic systems touches on some of the deepest issues in science and philosophy—order vs. chaos, randomness vs. determinacy, analysis vs. synthesis. The study of dynamic systems is not just a new research tool or new area of study for scientists. The study of dynamic systems stands as a new form of literacy for all, a new way of describing, viewing and symbolizing phenomena in the world. The language of the present mathematics and science curriculum employs static representations. Yet, our world is, of course, constantly changing. This disjunct between the world of dynamic experience and the world of static school representations stands as one source of student alienation from the current curriculum. The theoretical and computer-based tools arising out of the study of dynamic systems can describe and display the changing phenomena of science and the everyday world.
2.0 Dynamic Systems Modeling in the Connected Probability Project
The goal of the Connected Probability project (Wilensky 1995a; 1995b; 1997) is to study learners (primarily high school students) engaged in substantial investigations of stochastic phenomena. As part of the project, learners are provided with access to a wide variety of modeling tools which they can use in pursuit of their investigations. They are particularly encouraged to use the StarLogo (Resnick 1994; Wilensky 1995a) modeling language to conduct their investigations.
StarLogo is one of a new class of object-based parallel modeling languages (OBPML). The Resnick chapter in this book includes a detailed description of StarLogo. In brief, It is an extension of the Logo language in which a user controls a graphical turtle by issuing commands, such as "forward", "back", "left" and "right". In StarLogo, the user can control thousands of graphical turtles. Each turtle is a self-contained "object" with internal local state. Besides the turtles, StarLogo automatically includes a second set of objects, "patches". A grid of patches undergirds the StarLogo graphics window. Each patch is a square or cell that is computationally active. Patches have local state and can act on the "world" much like turtles. Essentially, a patch is just a stationary turtle. For any particular StarLogo model, there can be arbitrarily many turtles (from 0 to 32000 is typical in the StarLogo versions we have used), but there are a fixed number of patches (typically, 10,000 laid out in a 100x100 grid).
The modeling projects described in this chapter have run in several different versions of the StarLogo language on several different platforms. For simplicity of the exposition, all models will be described in their reimplemented form in the version of StarLogo called StarLogoT1, which is a Macintosh computer implementation -- an extension and superset of StarLogo2.02.
This chapter will describe in detail the evolution of a set of StarLogoT models for exploring the behavior of gases. We now call this collection of models GasLab. The original GasLab model was built, in the connection machine version of StarLogo, by a high school physics teacher involved in the Connected Probability project. He called the model GPCEE (Gas Particle Collision Exploration Environment). In the reimplementation of GPCEE for newer versions of StarLogo, the GPCEE model was renamed Gas-in-a-Box and it is one of an evolving collection of models that constitute GasLab.
3.0 The Creation of the Gas-in-a-Box Model -- Harry’s Story
In the context of the Connected Probability project, students were offered the opportunity to construct StarLogoT models of phenomena of interest to them that involved probability and statistics. Harry, a high school physics teacher enrolled in an education class that I was teaching, had long been intrigued by the behavior of a gas in a sealed container. He had learned in college that the gas molecule speeds were distributed according to a well known law, the Maxwell-Boltzmann distribution law. This distribution had a characteristic right-skewed shape. He had taught this law and its associated formula to his own students, but there remained a gap in his understanding -- how/why did this particular distribution come about? What kept it stable? To answer these questions, he decided to build (with my help3) a StarLogoT model of gas molecules in a box.
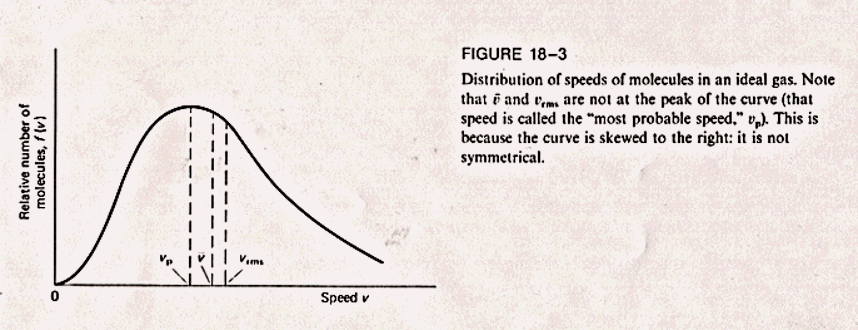
Figure 1: Maxwell-Boltzmann Distribution of Molecule Speeds (illustration from Giancoli, 1984)4
Harry built his model on certain classical physics assumptions:
• Gas molecules are modeled as spherical "billiard balls" -- in particular, as symmetric and uniform with no vibrational axes
• Collisions are "elastic" -- that is, when particles collide with the sides of the box or with other gas molecules, no energy is lost in the collision, all the energy is preserved as kinetic energy of the moving molecules.
• Points of collision between molecules are determined stochastically. It is reasonable to model the points of collision contact between particles as randomly selected from the surface of the balls.
Harry’s model displays a box with a specified number of gas particles randomly distributed inside it. The user can set various parameters for the particles: mass, speed, direction. The user can then perform "experiments" with the particles.
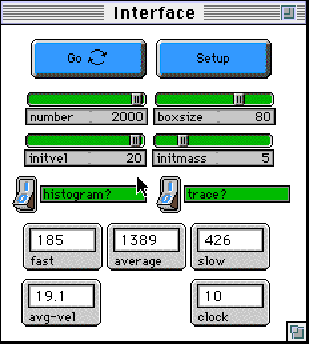
Figure 2: Gas-in-a-Box Interface Window
Harry called his program GPCEE (for Gas Particle Collision Exploration Environment), though other students have subsequently dubbed it "GasLab". Harry’s program was a relatively straightforward (though longish) StarLogoT program. At its core were three procedures which were executed (in parallel) by each of the particles in the box:
go
: the particle checks for obstacles and, if none are present, it moves forward (an amount based on its speed variable) for one clock tick.bounce
: if the particle detects a wall of the box, it bounces off the wall.collide
: if the particle detects another particle in its vicinity, the particles bounce off each other like billiard balls.Harry was excited by the expectation that the macroscopic laws of the gas should emerge, spontaneously, from the simple rules, at the microscopic level, he had written for the particles. He realized that he wouldn’t need to program the macro-level gas rules explicitly; they would come "for free" if he wrote the underlying (micro-level) particle rules correctly. He hoped to gain deeper explanatory understanding of and greater confidence in the gas laws through this approach — seeing them emerge as a consequence of the laws of individual particles and not as some mysterious orchestrated properties of the gas.
In one of his first experiments, Harry created a collection of particles of equal mass randomly distributed in the box. He initialized them to start at the same speed but moving in random directions. He kept track of several statistics of the particles on another screen. When looking at this screen, he noticed that one of his statistics, the average speed, was going down. This surprised him. He knew that the overall energy of the system should be constant: energy was conserved in each of the collisions. After all, he reasoned, the collisions are all elastic, so no energy is lost from the system. Since the number of molecules isn’t changing, the average energy or ![]() should also be a constant. But energy is just proportional to the mass and the square of the speed. Since the mass is constant for all molecules, the average speed should also be constant. Why, then, did the model output show the average speed to be decreasing? In Harry’s words:
should also be a constant. But energy is just proportional to the mass and the square of the speed. Since the mass is constant for all molecules, the average speed should also be constant. Why, then, did the model output show the average speed to be decreasing? In Harry’s words:
The IMPLICATION of what we discovered is that the average
length of each of the individual vectors does indeed go down.
PICTURE IT! I visualize little arrows that are getting smaller.
These mental vectors are just that. Little 2 (or 3)-dimensional arrows.
The move to the scalar is in the calculation of energy (with its v**2 terms.)
Doesn't it seem difficult to reconcile the arrows (vectors) collectively getting smaller with a scalar (which is a quantity that for a long time was visualized as a fluid) 'made up' from these little vectors NOT getting less!
Harry was dismayed by this new "bug" and set out to find what "had to" be an error in the code. He worked hard to analyze the decline in average speed to see if he could get insight into the nature of the calculation error he was sure was in the program.
But there was no error in the code. After some time unsuccessfully hunting for the bug, Harry decided to print out average energy as well. To his surprise, the average energy stayed constant.
At this point, Harry realized that the bug was in his thinking rather than in the code. To get a more visual understanding of the gas dynamics, he decided to color-code the particles according to their speed: particles are initially colored green; as they speed up, they get colored red; as they slow down, they get colored blue. Soon after starting the model running, Harry observed that there were many more blue particles than red particles. This was yet another way of thinking about the average-speed problem. If the average speed were indeed to drop, one would then observe more slow (blue) particles than fast (red) ones — so this was consistent with the hypothesis that the bug was in his thinking not in the code.
Harry now began to see the connection between the shape of the Maxwell-Boltzmann distribution and the visual representation he had created. The color-coding gave him a concrete way of thinking about the asymmetric Maxwell-Boltzmann distribution. He could "see" the distribution: initially, all the particles were green, a uniform symmetric distribution, but as the model developed, there were increasingly more blue particles than red ones, resulting in a skewed, asymmetric spread of the distribution.

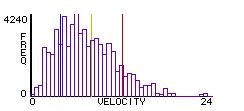
Figure 4: Dynamic histogram of molecule speeds after 30 clock ticks.
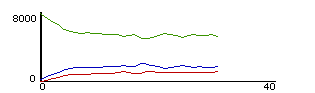
Figure 5: Dynamic plot of fast, slow and medium speed particles.
Even though Harry knew about the asymmetric Maxwell-Boltzmann distribution, he was surprised to see the distribution emerge from the simple rules he had programmed. Since he had himself programmed the rules, he was convinced that this stable distribution does indeed emerge from these rules. Harry tried several different initial conditions and all of them resulted in this distribution. He now believed that this distribution was not the result of a specific set of initial conditions, but that any gas, no matter how the particle speeds were initialized, would attain this stable distribution5. In this way, the StarLogoT model served as an experimental laboratory where the distribution could be "discovered." This type of experimental laboratory is not easily (if at all) reproducible outside of the computer-modeling environment.
But there remained several puzzles for Harry. Though he believed that the Maxwell-Boltzmann distribution emerged from his rules, he still did not see why they emerged. And he still did not understand how these observations squared with his mathematical knowledge — how could the average speed change when the average energy was constant?
Reflecting on this confusion gave Harry the insight he had originally sought from the GasLab environment. Originally, he had thought that, because gas particles collided with each other randomly, they would be just as likely to speed up as to slow down, so the average speed should stay roughly constant. But now, Harry saw things from the perspective of the whole ensemble. The law of conservation of energy guaranteed, Harry knew, that the overall pool of energy was constant. Although there were many fewer red particles than blue ones, Harry realized that each red particle "stole" a significant amount of energy from this overall pool of energy. The reason: energy is proportional to the square of speed, and the red particles were high speed. Blue particles, in contrast, took much less energy out of the pool. So each red particle need to be "balanced" by more than one blue particle to keep the overall energy constant. In Harry’s words:
There have to be more blue particles. If there were the same number of blues as reds then the overall energy would go up. Let’s say 1000 green particles have mass 1 and speed 2, then the overall energy is equal to 2000 [ED — 1/2 * m * V**2]. If half the greens become red at speed 3 and half become blue at speed 1, then the energy of the reds is 500 * 1/2 * 9 which equals 2250. (Wow, that’s already more than the total energy) and the energy of the blues is 500 * 1/2 * 1 which equals 250. Oh, yeah, I guess I don’t need the 500 there, a red is nine times as energetic as a blue so to keep the energy constant we need 9 blues for every red.
Harry was now confident that he had discovered the nugget of why the Maxwell-Boltzmann distribution arose. As particles collided they changed speeds and the energy constraint ensured that there would be more slow particles than fast ones. Yet, he was still puzzled on the "mathematical side". He saw that the greater number of blue particles than red particles ensured that the average speed of the molecules would indeed decrease from the initial average speed of a uniform gas. But, how did this square with the mathematical formulas?
Harry had worked on the classical physics equations when he felt sure there was a bug in the StarLogoT code. He had worked on them in two different ways and both methods led to the conclusion that the average speed should be constant. What was wrong with his previous reasoning?
In his first method, he had started with the assumption that momentum6 is conserved inside the box. Since mass is constant, this means the average velocity as a vector is constant. Since the average velocity is constant, he had reasoned that its magnitude, the average speed, had to be constant as well. But, now he saw that this reasoning was faulty, in his words:
[I] screwed up the mathematics – the magnitude of the average vector is not the average speed. The average speed is the average of the magnitudes of the vectors. And the average of the magnitudes is not equal to the magnitude of the average.
In his second method, he began with the assumption that the energy of the ensemble would be constant. This could be written ![]() is constant. Factoring out the constant terms, it follows that
is constant. Factoring out the constant terms, it follows that ![]() is a constant . From this he had reasoned that the average speed,
is a constant . From this he had reasoned that the average speed, ![]() , would also have to be constant. He now saw the error in that mathematics as well. It is not hard to show that if the former sum (corresponding to energy) is constant then the latter sum (corresponding to speed) is maximal under the uniform initial conditions. As the speeds diverge, the average speed decreases just as he "observed". For a fixed energy, the maximum average speed would be attained when all the speeds were the same as they were in the initial state. From then on, more particles would slow down than would speed up.
, would also have to be constant. He now saw the error in that mathematics as well. It is not hard to show that if the former sum (corresponding to energy) is constant then the latter sum (corresponding to speed) is maximal under the uniform initial conditions. As the speeds diverge, the average speed decreases just as he "observed". For a fixed energy, the maximum average speed would be attained when all the speeds were the same as they were in the initial state. From then on, more particles would slow down than would speed up.
Although both these bugs were now obvious to Harry and he felt that they were "embarrassing errors for a physics teacher to make", this confusion between the vector and scalar averages was lurking in the background of his thinking. Once brought to light, it could readily be dispensed with through standard high school algebra. However, the standard mathematical formalism did not cue Harry into seeing his errors. His confusion was brought to the surface (and led to increased understanding) through constructing and immersing himself in the Gas-in-a-Box model. In working with the model, it was natural for him to ask questions about the large ensemble and to get experimental and visual feedback. This also enabled Harry to move back and forth between different conceptual levels, the level of the whole ensemble, the gas, and the level of individual molecules.
Harry was now satisfied that the average speed of the ensemble would indeed decrease from its initial uniform average. The above reasoning relieved his concerns about how such an asymmetric ensemble could be stable. But it had answered his question only at the level of the ensemble. What was going on at the level of individual collisions? Why were collisions more likely to lead to slow particles than fast ones? This led him to conduct further investigations into the connection between the micro- and macro- views of the particle ensemble.
Harry was led inexorably to the question: why would the particle speeds spread out from their initial uniform speed? Indeed, why do the particles change speed at all? When teased out, this question could be framed as: "The collisions between particles are completely symmetric – why, then, does one particle change speed more than the other? To answer this question, Harry conducted further modeling experiments, repeating collisions of two particles in fixed trajectories. After seeing two particles collide at the same angle again and again, but emerging at different angles each time, he remembered that "randomness was going on here". The particles were choosing random points on their surface to collide, so they did not behave the same way each time. By experimentally varying the collision points, he observed that the average speed of the two particles did not usually stay constant. Indeed, it remained constant only when the particles collided head-on.
It was not long from this realization to the discovery of the broken symmetry: "when particles collide, their trajectories may not be symmetrical with respect to their collision axis. The apparent symmetry of the situation is broken when the particles do not collide head-on — that is, when their directions of motion do not have the same relative angle to the line that connects their centers.

Figure 6: Broken symmetry leads to changing speeds.
Harry went on to do the standard physics calculations that confirmed this experimental result. In a one-dimensional world, he concluded, all collisions would be head on and, thus, average speed would stay constant7; in a multi-dimensional world, particle speed distributions become non-uniform and this leads inevitably to the preponderance of slower particles and the characteristic asymmetric distribution.
Harry had now adopted many different views of the gas and used many different methods to explain the asymmetry of the particle speed distribution. Through connecting the macro-view of the particle ensemble with the micro-view of the individual particle collisions, he had come to understand both levels of description in a deeper way. Through connecting the mathematical formalism to his observations of colored particle distributions, he had caught errors he had made on the "mathematical side" and, more importantly, anchored the formalism in visual perception and intuition. Harry felt he had gained great explanatory power through this connection of the micro- and macro- views. This connection was made feasible through the support offered by the StarLogoT modeling language.
When asked what he had learned from the experience of building the Gas-in-a-box model, Harry made one more trenchant observation. He had found that the average speed of the gas molecules was not constant. Upon reflection, he realized:
Of course the average speed is not constant. If it were constant, I’d have known about it. It isn’t easy to be a constant and that’s why we have named laws when we find constants or invariants. The law of conservation of energy guarantees that the energy of the gas is a constant. We do not have a law of conservation of speed.
Harry now understood the concept of energy in a new way. He saw that energy could be seen as a statistical measure of the ensemble that was invariant. He saw that there could be many statistical measures that characterize an ensemble -- each of them could lay claim to being a kind of "average", that is, a characteristic measure of the ensemble. The idea of "average" is then seen to be another method for summarizing the behavior of an ensemble. Different averages are convenient for different purposes. Each has certain advantages and disadvantages, certain features that it summarizes well and others that it does not. Which average we choose or construct depends on which aspects of the data we see as important. Energy, he now saw, was a special such average, not, as he had sometimes wondered before, a mysteriously chosen formula, but rather a measure that characterized invariantly the collection of particles in a box.
4.0 Creation of the GasLab Toolkit -- Extensible Models
After Harry finished working with the Gas-in-a-Box model, I decided to test the model with students who had not been involved in its development. I contacted a local high school and arranged to meet three hours a week for several weeks with a few juniors and seniors taking introductory physics. The group was somewhat fluid, consisting of three regular members with 3 - 4 others sometimes dropping in. The students who chose to be involved did so out of interest. Their teacher described the 3 regular members as "average to slightly above average" physics students. I introduced the students to the Gas-in-a-Box model, showed them how to run the model and how to change elementary parameters of the model. I asked them to begin by just "playing" with the model and talking to me about what they observed. I describe below these students’ experience with GasLab. I have introduced GasLab to dozens of groups of students (high school and collegiate) since that time. While the details of their explorations are quite different in each case, the overall character of the model-based inquiry is typified by the story related below.
The students worked as a group, one of them "driving" the model from the keyboard with others suggesting experiments to try. One of the first suggested experiments was to put all of the particles in the center of the box8. This led to a pleasing result as the gas "exploded" in rings of color, a red ring on the outside, with a nested green ring and a blue ring innermost. The students soon hit upon the same initial experiment that stimulated Harry. They started with a uniform distribution of 8000 green particles and immediately wondered at the preponderance of blue particles over red particles as the simulation unfolded. Over the next week, they went through much of the same reasoning that Harry had gone though connecting the energy economy of the gas particle ensemble with the speed distribution of the particles.
But these students were not as motivated by this question as was Harry. One student, Albert, became very excited by the idea that the micro-model should reproduce the macroscopic gas laws:
What’s really cool is that this is it. If you just let this thing run then it’ll act just like a real gas. You just have to start it out right and it’ll do the right thing forever. We could run experiments on the computer and the formulas we learned would come out.
Albert went on to suggest that since this was a real gas, they could verify the ideal gas laws for the model. The group decided to verify Boyle’s law -- that changing the volume of the box would lead to a reciprocal change in the pressure of the gas.
Now the group was faced with creating an experiment that would test whether Boyle’s law obtained in the GasLab model. Tania made a suggestion:
We could make the top of the box move down like a piston. We’ll measure the pressure when the piston is all the way up. Then we’ll let it fall to half way down and measure the pressure again. The pressure should double when the piston is half way down.
The group agreed that this was a reasonable methodology, but then they were stopped short by Isaac who asked: "How do we measure the pressure"? This question was followed by a substantial pause. They were used to being given an instrument to measure pressure, a black box from which they could just read out a number. As Albert said for the group: "We have to invent a pressure-measure, a way of saying what the pressure is in terms of the particles". The group pondered this question. At their next meeting, Tania suggested the first operational measure:
We could have the sides of the box9 store how many particles hit them at each tick. The total number of particles hitting the sides of the box at each tick is our measure of pressure.
They programmed this measure of pressure into the model. Lots of discussion ensued as to what units this measure of pressure represented. At long last, they agreed that they did not really care what the units were. All they needed to know, in order to verify Boyle’s law, was that the measure would double, so a unit scale factor would not affect the result of the experiment.
They created a "monitor" that would display the pressure in the box and ran the model. To their dismay, the pressure in the box fluctuated wildly. Tania was quick to point out the problem:
We only have 8000 particles in the box. Real boxes full of gas have many more particles in them. So the box is getting hit a lot less times at each tick than it should be. I think what’s happening is that the number of particles isn’t big enough to make it come out even.
Persuaded by this seat-of-the-pants "law of large numbers" argument, they made an adjustment to the pressure measuring code. They calculated the number of collisions at each tick over a number of ticks, then averaged them. Trial and error simulations varying the averaging time interval convinced them that averaging over ten ticks led to a sufficiently stable measure of pressure.
Now that they had a stable pressure gauge, they were ready to construct the piston and run the experiment. But, here again, they ran into conceptual difficulties. How was the piston to interact with the particles? Were they to model it as a large, massive particle that collided with the particles? In that case, how massive should it be? And, if they did it that way, wouldn’t it affect the pressure in the box in a non-uniform way? As Albert said:
If we do the piston, then the North-South pressure in the box will be greater than the East-West pressure. That doesn’t seem right. Shouldn’t the pressure in the box stay even?
This issue was discussed, argued and experimented on for several hours. It was at this point that Tania suggested another approach.
I’m confused by the effect the piston is supposed to have on the particles. I have an idea. Why don’t we start the particles out in half the box, then release the "lid" and let them spread out into the whole box. If we do that, we won’t have to think about pistons and we can just see if the pressure decreases in half.
The group agreed that this was a promising approach and quickly implemented this code. They were now able to run the experiment that they hoped would confirm Boyle’s law. Their experiment worked as they hoped. When they lifted the lid so that the box had double the volume, the pressure in the box did, indeed, drop in half.

Figure 7: Box with lid down -- volume = 1200. Box with lifted lid -- volume = 2400. Lifting box lid proportionally reduces pressure.
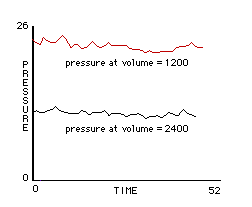
Figure 8: Plot of pressure as measured in the box at the two different volumes.
This confirming result could have led to an unfortunate acceptance of Tania’s measure of pressure as accurate. Indeed, experimental results with this isothermal version of Boyle’s law could not have disconfirmed Tania’s measure. However, in time, the students did come to reject this measure on conceptual grounds. They reasoned that heavier particles ought to make more of a difference in the pressure than lighter ones. Similarly, they reasoned that faster particles should have more effect than slower ones. This led them to revise their pressure measure to the conventional physics definition -- momentum transfer to the sides of the box per unit time.
Their escapade with Tania’s definition, however, did yield insights. As Tania later said:
I guess for Boyle’s law to work, all that matters is how dense the molecules are in the box. With more space they’re less likely to collide so the pressure drops.
There is another incident of note surrounding the Boyle’s law experiment. A week or so after completing the experiment, Isaac ran the model again with all particles initialized to be at the center of the box. While watching his favorite "explosion", Isaac noted that the gas pressure registered 0! Quickly, he realized that that was a consequence of their definition -- no particles were colliding with the sides of the box. Somehow, this didn’t seem right to Isaac and led him to ask the group if they should revise their concept of pressure yet again. Argumentation ensued as to "whether a gas had internal pressure without any box to measure it". They realized that the experiment in question was not feasible in a real experimental setting, but nonetheless, it did seem that there should be a theoretical answer to the question. Isaac suggested various ingenious solutions to the problem, but in the end, the group did not alter their pressure gauge. The ingenious solutions were difficult to implement and their current gauge seemed to be adequate to the experiments they were conducting.
One more noteworthy development was related to the emergence of the Maxwell-Boltzmann distribution discussed in the previous section. Albert came in one day excited about an insight he had had. The gas molecules, he said, can be thought of as probabilistic elements, like dice. They can randomly go faster or slower. But while there is no real limit to how fast they can go10, their speed is bounded below by zero. It’s as if particles were conducting a random walk on the plane but there was a wall on the y-axis. Albert saw that this constrained random walk would have to produce a right-skewed distribution. I challenged him to go further: a) Could he construct a StarLogoT model to prove his theory? b) Could he determine what particular probability constraints would produce a strict Maxwell-Boltzmann distribution? c) Could he find other seemingly unrelated phenomena that satisfied the same formal constraints and thus would also produce a Maxwell-Boltzmann distribution? Albert and his fellow students were up to these challenges.
These students (and subsequent groups of students) have conducted many more experiments with the Gas-in-a-Box model. Through revising and extending the model, they created a set of models that has since been expanded into the toolkit we now call GasLab. The set of extensions of the original Gas-in-a-Box model is truly impressive in its scope and depth of conceptual analysis. Among the many extensions they tried were: heating and cooling the gas, introducing gravity into the model (and a very tall box) and observing atmospheric pressure and density, modeling the diffusion of two gases, allowing the top to be porous and seeing evaporation, relaxing elasticity constraints while introducing weak attraction and looking for phase transitions, introducing vibrations into the container and measuring sound density waves, and allowing heat to escape from the box into the surrounding container. Over the course of several weeks, these high school students "covered" much of the territory of collegiate statistical mechanics and thermal physics. Their understanding of it was deeply grounded in both a) their intuitive understandings gained from their concrete experience with the models and b) the relations among the fundamental concepts.
GasLab provides learners with a set of tools for exploring the behavior of an ensemble of micro-level elements. Through running, extending and creating GasLab models, learners were able to develop strong intuitions about the behavior of the gas at the macro level (as an ensemble gas entity) and its connections to the micro level (the individual gas molecule). In a typical physics classroom, learners usually address these levels at different times. When attending to the micro level, the focus is, typically, on the exact calculation of the trajectories of two colliding particles. When attending to the macro level, the focus is on "summary statistics" such as pressure, temperature, and energy. Yet, it is in the connection between these two primary levels of description that the explanatory power resides.
Two major factors enable students using GasLab to make the connection between these levels -- the replacement of symbolic calculation with simulated experimentation and the replacement of "black-box" summary statistics with learner-constructed summary statistics. The traditional curriculum segregates the micro- and macro- levels of description because the mathematics required to meaningfully connect them is thought to be out of reach of high school students. In the GasLab modeling toolkit, the formal mathematical techniques can be replaced with concrete experimentation with simulated objects. This experimentation allows learners to get immediate feedback about their theories and conjectures. The traditional curriculum hands learners summary statistics such as pressure as "received" physics knowledge. It is a "device" built by an expert, which the learner cannot inspect nor question. Most fundamentally, the learner has no access to the design space of possibilities from which this particular design was selected. In the GasLab context, learners must construct their own summary statistics. As a result, the traditional pressure measure is seen to be one way of summarizing the effect of the gas molecules on the box, one way to build a pressure gauge. The activity of designing a pressure measure is an activity of doing physics, not absorbing an expert’s "dead" physics.
The two factors described above (the ability to act on the model and to "see" its reactions, and the ability to create interpretations of the model in the form of new computational objects which, in turn, can be acted upon) make a significant difference in the kinds of understandings students can construct of the behavior of gas molecule ensembles. Through engaging with GasLab, high-school students have access to the powerful ideas and explanations of statistical thermal physics. Yet, by engaging in such activities, the students came to understand the gas as a concrete entity, much in the same way they experience physical entities outside the computer. These constructive modeling and model-based reasoning activities can provide students a concrete understanding, and a powerful way of apprehending, the physics and chemistry of gases—one that eludes even some professional scientists who learned this content in a traditional manner.
5.0 Implications for the Pedagogy of Modeling
Despite the rapid rate of infiltration of computer-based modeling and dynamics systems theory into scientific research and into popular culture, computer-based modeling has only slowly begun to impact education communities. While computer-based models are increasingly used in the service of pedagogic ends (Buldyrev et al 1994; Chen & Stroup 1993; Doerr 1996; Feurzeig 1989; Horwitz 1989; Horwitz et al 1994; Jackson et al 1996; Mandinach & Cline 1994; Mellar et al 1994; Roberts et al 1983; Repenning 1994; Shore et al 1992; Smith et al 1994; White & Frederiksen 1998; Wilensky, 1997; Wilensky & Resnick, in press), there remains significant lack of consensus about the proper role of modeling within the curriculum.
5.1 Model Construction versus Model Use
One tension that is felt is between students using already-constructed models of phenomena versus students constructing their own models to describe phenomena. At one extreme is the use of pre-constructed models purely for demonstration of phenomena. This use of modeling employs the computer to animate and dynamically display the structures and processes that describe the phenomena. It may permit students to modify the model’s inputs and parameters, but it does not enable students to modify the model’s structures, processes, or operation. At the other extreme, learners are involved in constructing their own models of phenomena de nova. Between these extremes are other kinds of modeling activities: one of particular interest is student use of pre-constructed models as investigative tools for model-based inquiry -- activities that may involve learner modification and extension of the initial models provided to them11. Here, students are given starting models but are also involved in model design and development.
For the use of models to provide demonstrations, I employ the term "demonstration modeling". While such demonstration models can be visually striking, they are not very different from viewing a movie of the phenomenon in question. The computational medium is being used merely for delivery. From a constructivist point of view, this delivery model is unlikely to lead to deep learning, as it does not engage with the learner’s point of entry into the phenomena to-be-understood. Nor does this approach take advantage of the computer’s interactivity to give the learner a chance to probe the model and get the feedback necessary to construct mental models of the phenomena observed.
Constructivists might be happier with the "from scratch" modeling activity as it requires the learner to start where she is and interact with the modeling primitives to construct a model of the phenomenon. That special breed of constructivist called constructionists (Papert, 1991) would argue that this externalized construction process is the ideal way to engage learners in constructing robust mental models. The learner is actively engaged in formulating a question, formulating tentative answers to her question and through an iterative process of reformulation and debugging, arriving at a theory of how to answer the question instantiated in the model. This process is an act of doing and constructing mathematics and science instead of viewing the results of an expert’s having done the mathematics and science and handing it off to the learner. On the epistemological side, this lesson that mathematics and science are ongoing activities in which ordinary learners can be creative participants is an important meta-lesson of the modeling activity. These considerations can be summarized in the table given below:
Model Use (Demonstration Models) Model Construction (Model Based Inquiry)
|
passive |
active |
|
viewing a "received" mathematics and science |
constructing mathematics and science |
|
transmission of ideas |
expression of ideas |
|
dynamic medium used for viewing output of mathematical thought |
dynamic medium used as executor of mathematical thought |
|
an expert's question |
learner's own question |
|
an expert's solution |
learner's own tentative solution |
|
learning in single step |
learning through debugging |
|
experts must anticipate relevant parameters for learning |
learners can construct parameters relevant to their learning |
An argument on the side of using demonstration models is that the content to be learned is placed immediately and directly to the attention of the learner. In contrast, in the process of constructing a model, the learner is diverted into the intricacies of the modeling language itself and diverted away from the content to be learned. Since there can be quite a bit of overhead associated with learning the modeling language, the model construction approach could be seen as very inefficient. Moreover, there is skepticism as to whether students who are not already mathematically and scientifically sophisticated can acquire the knowledge and skills of model design and construction.
5.2 Selecting the Appropriate "Size" of Modeling Primitives
Like most tensions, this tension is not really dichotomous. There are many intermediate states between the two extremes. Demonstration models can be given changeable parameters which users can vary and, thereby, explore the effect on the behavior of the model. If there are large numbers of such parameters, as in the popular Maxis simulation software packages (1992a; 1992b), the parameter space can be quite vast in the possibilities for exploration. This takes demonstration models several steps in the direction of model construction. On the other hand, even the most from "scratch" modeling language must contain primitive elements. These primitive elements remain black boxes, used for their effect but not constructed by the modeler. Not too many constructionist modelers would advocate building the modeling elements from the binary digits, let alone building the hardware that supports the modeling language. The latter can serve as an absurd reductio of the "from scratch" label. So, even the die-hard constructionist modelers concede that not all pieces of the model need be constructed, some can be simply handed off.
I place myself squarely in the constructionist camp; the challenge for us is to construct toolkits that contain just the right level of primitives. In constructing a modeling language, it is critical to design primitives not so large-scale and inflexible that they can only be put together in a few possible ways. If we fail at that task, we have essentially reverted to the demonstration modeling activity. To use a physical analogy, we have not done well in designing a dinosaur modeling kit if we provide the modeler with three pieces, a T-Rex head, body and tail. On the other hand, we must design our primitives so that they are not so "small" that they are perceived by learners as far removed from the objects they want to model. If we fail at that task, learners will be focused at an inappropriate level of detail and so will learn more about the modeling pieces than the content domain to be modeled. To reuse the physical analogy, designing the dinosaur modeling kit to have pieces that are small metal bearings may make constructing many different kinds of dinosaurs possible, but it will be tedious and removed from the functional issues of dinosaur physiology that form the relevant content domain.
This places modeling language (and model) designers face to face with the characteristics of the primitive modeling elements to be given to learners. Modeling language designers that choose to make their primitive elements on the large side, we call demonstration modeling designers, whereas those who tend to keep their primitives small, we call constructionist modeling designers. Demonstration modeling designers have no choice but to make the pieces, from which the models are built, semantically interpretable from within the model content domain. Constructionist modeling designers, though, can make the underlying model elements content neutral12, thus creating a modeling language that is general-purpose, or they can choose modeling elements that have semantic interpretation in a chosen content domain, thus creating a modeling toolkit for that content domain.
5.3 General Purpose vs. Content Domain Modeling Languages
Both of these choices, content domain modeling languages and general-purpose modeling languages, can lead to powerful modeling activities for learners. The advantage of the content domain modeling language is that learners can enter more directly into substantive issues of the domain (issues that will seem more familiar to them and to their teachers). The disadvantage is that the primitive elements of the language, which describe important domain content, are opaque to the learner. Another disadvantage is that use of the language is restricted to its specific content domain. That disadvantage may be nullified by designing a sufficiently broad class of such content domain modeling languages, though maintaining such a broad class may be challenging. The advantage of the content-neutral primitives is that all content domain structures, since they are made up of the general purpose elements, are inspectable, constructible and modifiable by the learner. The disadvantage is that the learner must master a general purpose syntax before being able to make headway on the domain content. What is needed is a way for learners to be able to begin at the level of domain content, but not be limited to unmodifiable black-box primitives.
In the Connected Probability project, the solution we have found to this dilemma is to build so-called "extensible models" (Wilensky, 1997). In the spirit of Eisenberg’s programmable applications (Eisenberg, 1991), these models are content-specific models that are built using the general-purpose StarLogoT modeling language. This enables learners to begin their investigations at the level of the content. Like the group of high schoolers described in the earlier section of this chapter, they begin by inspecting a pre-built model such as Gas-in-a-Box. They can adjust parameters of the model such as mass, speed, location of the particles and conduct experiments readily at the level of the content domain of ideal gases. But, since the Gas-in-a-Box model is built in StarLogoT, the students have access to the workings of the model. They can "look under the hood" and see how the particle collisions are modeled. Furthermore, they can modify the primitives, investigating what might happen if, for example, collisions are not elastic. Lastly, students can introduce new concepts, such as pressure, as primitive elements of the model and conduct experiments on these new elements.
This extensible modeling approach allows learners to dive right into the model content, but places neither a ceiling on where they can take the model nor a floor below which they cannot see the content. Mastering the general purpose modeling language is not required at the beginning of the activity, but happens gradually as learners seek to explain their experiments and extend the capabilities of the model.
When engaged in classroom modeling, the pedagogy used in the Connected Probability project has four basic stages: In the first stage, the teacher presents a "seed" model to the whole class. Typically, the seed model is a short piece of StarLogoT code that captures a few simple rules. The model is projected through an LCD panel so the whole class can view it. The teacher engages the class in discussion as to what is going on with the model. Why are they observing that particular behavior? How would it be different if model parameters were changed? Is this a good model of the phenomenon it is meant to simulate? In the second stage, students run the model (either singly or in small groups) on individual computers. They engage in systematic search of the parameter space of the model. In the third stage, each modeler (or group) proposes an extension to the model and implements that extension in the StarLogoT language. Modelers that start with Gas-in-a-Box, for example, might try to build a pressure gauge, a piston, a gravity mechanism or heating/cooling plates. The results of this model extension stage are often quite dramatic. The extended models are added to the project’s library of extensible models and made available for others to work with as seed models. In the final stage, students are asked to propose a phenomenon, and to build a model of it from "scratch", using the StarLogoT modeling primitives.
5.4 Phenomena-based vs. Exploratory Modeling
When learners are engaged in creating their own models, two primary avenues are available. A modeler can choose a phenomenon of interest in the world and attempt to duplicate that phenomenon on the screen. Or, a modeler can start with the primitives of the language and explore the possible effects of different combinations of rules sets. The first kind of modeling, which I call phenomena-based modeling (Wilensky 1997; Resnick & Wilensky 1998) is also sometimes called backwards modeling (Wilensky 1997) because the modeler is engaged in going backwards from the known phenomenon to a set of underlying rules that might generate that phenomenon. In the GasLab example, Harry knew about the Maxwell-Boltzmann distribution and tried creating rules which he hoped would duplicate this distribution. In this specific case, Harry did not have to discover the rules himself because he also knew the fundamental rules of Newtonian mechanics which would lead to the Maxwell-Boltzmann distribution. The group of students who worked on modeling Boyle’s law came closer to pure phenomena-based modeling as they tried to figure out the "rules" for measuring pressure. Phenomena-based modeling can be quite challenging as discovering the underlying rule-sets that might generate a phenomenon is inherently difficult -- a fundamental activity of science practice. In practice, most GasLab modelers mixed some knowledge of what the rules were supposed to be with adjustments to those rules when the desired phenomenon did not appear.
The second kind of modeling, which I call exploratory modeling (Wilensky 1997; Resnick & Wilensky 1998) is sometimes called "forwards" modeling (Wilensky 1997) because modelers start with a set of rules and try to work forwards from these rules to some, as yet, unknown phenomenon.
5.5 New Forms of Symbolization
In a sense, modeling languages are always designed for phenomena-based modeling. However, once such a language exists, it also becomes a medium of expression in its own right. Just as, we might speculate, natural languages originally developed to communicate about real world objects and relations, but, once they were sufficiently mature, were also used for constructing new objects and relations. Similarly, learners can explore sets of rules and primitives of a modeling language to see what kinds of emergent effects may arise from their rules. In some cases, this exploratory modeling may lead to emergent behavior that resembles some real world phenomenon and, then, phenomena-based modeling resumes. In other cases, though the emergent behavior may not strongly connect with real world phenomena, the resulting objects or behaviors can be conceptually interesting or beautiful in themselves. In these latter cases, in effect, the modelers have created new phenomena, objects of study that can be viewed as new kinds of mathematical objects--objects expressed in the new form of symbolization afforded by the modeling language.
5.6 Aggregate vs. Object-based Modeling
In the previous section, we discussed the selection of modeling language primitives in terms of size and content-neutrality. Yet another distinction is in the conceptual description of the fundamental modeling unit. To date, modeling languages can be divided into two kinds: so-called "aggregate" modeling engines (e.g., STELLA (Richmond & Peterson 1990), Link-It (Ogborn 1994), VenSim, Model-It (Jackson et al 1996)) and "object-based" modeling languages (e.g., StarLogo (Resnick 1994; Wilensky 1995a), Agentsheets (Repenning 1993), Cocoa (Smith et al 1994), Swarm (Langton & Burkhardt 1997), and OOTLs (Neumann et al 1997)). Aggregate modeling languages use "accumulations" and "flows" as their fundamental modeling units. For example, a changing population of rabbits might be modeled as an "accumulation" (like water accumulated in a sink) with rabbit birth rates as a "flow" into the population and rabbit death rates as a flow out (like flows of water into and out of the sink). Other populations or dynamics -- e.g., the presence of "accumulations" of predators -- could affect these flows. This aggregate based approach essentially borrows the conceptual units, its parsing of the world, from the mathematics of differential equations.
The second kind of tool enables the user to model systems directly at the level of the individual elements of the system. For example, our rabbit population could be rendered as a collection of individual rabbits each of which has associated probabilities of reproducing or dying. The object-based approach has the advantage of being a natural entry point for learners. It is generally easier to generate rules for individual rabbits than to describe the flows of rabbit populations. This is because the learners can literally see the rabbits and can control the individual rabbit’s behavior. In StarLogoT, for example, students think about the actions and interactions of individual objects or creatures. StarLogoT models describe how individual creatures (not overall populations) behave. Thinking in terms of individual creatures seems far more intuitive, particularly for the mathematically uninitiated. Students can imagine themselves as individual rabbits and think about what they might do. In this way, StarLogoT enables learners to "dive into" the model (Ackermann 1996) and make use of what Papert (1980) calls "syntonic" knowledge about their bodies. By observing the dynamics at the level of the individual creatures, rather than at the aggregate level of population densities, students can more easily think about and understand the population dynamics that arise. As one teacher comparing students’ work with both STELLA and StarLogoT models remarked: When students model with STELLA, a great deal of class time is spent on explaining the model, selling it to them as a valid description. When they do StarLogoT modeling, the model is obvious; they do not have to be sold on it."
There are now some very good aggregate computer modeling languages—such as STELLA (Richmond & Peterson 1990) and Model-It (Jackson et al. 1996). These aggregate models are very useful—and superior to object-based models in some contexts, especially when the output of the model needs to be expressed algebraically and analyzed using standard mathematical methods. They eliminate one "burden" of differential equations -- the need to manipulate symbols-- focusing, instead on more qualitative and graphical descriptions of changing dynamics. But, conceptually, they still rely on the differential equation epistemology of aggregate quantities.
Some refer to object-based models as "true computational models," (Wilensky & Resnick, in press) since they use new computational media in a more fundamental way than most computer-based modeling tools. Whereas most tools simply translate traditional mathematical models to the computer (e.g., numerically solving traditional differential-equation representations), object-based languages such as StarLogoT provide new representations that are tailored explicitly for the computer. Too often, scientists and educators see traditional differential-equation models as the only approach to modeling. As a result, many students (particularly students alienated by traditional classroom mathematics) view modeling as a difficult or uninteresting activity. What is needed is a more pluralistic approach, recognizing that there are many different approaches to modeling, each with its own strengths and weaknesses. A major challenge is to develop a better understanding of when to use which approach, and why.
5.7 Concreteness vs. Formalism
Paradoxically, computer-based modeling has been critiqued both as being too formal and of being not formal enough. On the one hand, some mathematicians and scientists have criticized computer models as insufficiently rigorous. As discussed in the previous section, it is somewhat difficult, for example, to get a hold of the outputs of a StarLogoT model in a form that is readily amenable to symbolic manipulation. Moreover, there is as yet no formal methodology for verifying the results of a model run. Even in highly constrained domains, there is not a formal verification procedure for guaranteeing the results of a computer program; much less any guarantee that the underlying assumptions of the modeler are accurate. Computational models, in general, are subject to numerical inaccuracies dictated by finite precision. Object-based models, in particular, are also vulnerable to assumptions involved in transforming a continuous world into a discrete model. These difficulties lead many formalists to worry about the accuracy, utility and especially the generality of a model-based inquiry approach (Wilensky 1996). These critiques raise valid concerns, concerns that must be reflected upon as an integral part of the modeling activity. As we recall, Harry had to struggle with just such an issue when he was unsure whether the drop in the average speed of the gas particles was due to a bug in his model code or due to a "bug" in his thinking. It is an inherent part of the computer modeling activity to go back and forth between questioning the model’s faithfulness to the modeler’s intent (e.g., code bugs) and questioning the modeler’s expectations for the emergent behavior (e.g., bugs in the model rules). Though the formalist critic may not admit it, these limitations are endemic to modeling -- even using formal methods such as differential equations. Only a small set of the space of differential equations is amenable to analytic solution. Most modifications of those equations lead to equations that can only be solved through numerical techniques. The game for formal modeling, then, becomes trying to find solvable differential equations that can be said to map onto real world phenomena. Needless to say, this usually leads to significant simplifications and idealizations of the situation. The classic Lotka-Volterra equations (Lotka 1925), for example, which purport to describe the oscillations in predator/prey populations assume that birth rates and death rates are numerically constant over time. This assumption, while reasonable to a first approximation, does not hold in real world populations -- and, therefore, the solution to the differential equations is unlikely to yield accurate predictions. A stochastic model of predator/prey dynamics built in an object-based language will not produce a formal equation, but may produce better predictions of real world phenomena. Moreover, since object-based models are capable of refinement at the level of rules, adjusting them is also more clearly an activity of trying to successively refine content-based rules until they yield satisfactory results.
In contrast to the formalist critique, educator critics of computer-based modeling have expressed concern that the activity of modeling on a computer is too much of a formal activity, removing children from the concrete world of real data. While it is undoubtedly true that children need to have varied and rich experiences away from the computer, the fear that computer modeling removes the child from concrete experience with phenomena is overstated. Indeed, the presence of computer modeling environments invites us to reflect on the meaning of such terms as concrete experience (Wilensky 1991). We have come to see that those experiences we label "concrete" acquire that label through mediation by the tools and norms of our culture. As such, which experiences are perceived as concrete is subject to revision by a focused cultural and/or pedagogic effort. This is particularly so with respect to scientific content domains in which categories of experience are in rapid flux and in which tools and instruments mediate all experience. In the GasLab case, it would be quite difficult to give learners "real-world" experience with the gas molecules. A real world GasLab experience would involve apparatus for measuring energy and pressure that would be black-boxes for the students using them. The range of possibilities for experiments that students could conduct would be much more severely restricted and would most probably be limited to the "received" experiments dictated by the curriculum. Indeed, in a significant sense, the computer-based GasLab activity gives students a much more concrete understanding of the gas, seeing it as a macro- object that is emergent from the interactions of large numbers of micro- elements.
Concluding Remarks
The use of model-based inquiry has the potential for significant impact on learning in the next century. We live in an increasingly complex and interconnected society. Simple models will no longer suffice to describe that complexity. Our science, our social policy and the requirements of an engaged citizenry require an understanding of the dynamics of complex systems and the use of sophisticated modeling tools to display and analyze such systems. There is a need for the development of increasingly sophisticated tools that are designed for learning about the dynamics of such systems and a corresponding need for research on how learners, using these tools, begin to make sense of the behavior of dynamic systems. It is not enough to simply give learners modeling tools. Careful thought must be given to the conceptual issues that make it challenging for learners to adopt a systems dynamics perspective. The notion of levels of description, as in the micro- and macro- levels we have explored in this chapter, is central to a systems dynamics perspective, yet is quite foreign to the school curriculum. Behavior such as negative and positive feedback, critical thresholds, dynamic equilibria are endemic to complex dynamic systems. It is important to help learners build intuitions and qualitative understandings of such behaviors. Side by side with modeling activity, there is a need for discussion, writing, reflection activities that encourage students to reexamine some of the basic assumptions embedded in the science and mathematics curriculum: assumptions that systems can be decomposed into isolated sub-systems, that causes add up linearly and have deterministic effects. In the Connected Probability project, we have seen, for example, the ‘deterministic mindset’ (Wilensky 1997; Resnick & Wilensky 1998) prevent students from understanding how stable properties of the world, such as Harry’s Maxwell-Boltzmann distribution, can result from probabilistic underlying rules.
A pedagogy that incorporates the use of object-based modeling tools for sustained inquiry has considerable promise to address such conceptual issues. By providing a substrate in which learners can embed their rules for individual elements and visualize the global effect, it invites them to connect micro-level simulation with macro-level observation. By allowing them to control the behavior of thousands of objects in parallel, it invites them to see probabilism underlying stability and statistical properties as useful summaries of the underlying stochasm. By providing visual descriptions of phenomena that are too small or too large to visualize in the world, they invite a larger segment of society to make sense of such phenomena. By providing a medium in which dynamic simulations can live and which responds to learner conjectures with meaningful feedback, it gives many more learners the experience of doing science and mathematics. A major challenge is to develop tools and pedagogy that will bring this new form of literacy to all.
Acknowledgments
The preparation of this paper was supported by the National Science Foundation (Grants RED-9552950, REC-9632612), The ideas expressed here do not necessarily reflect the positions of the supporting agency. I would like to thank Seymour Papert for his overall support and inspiration and for his constructive criticism of this research in its early stages. Mitchel Resnick and David Chen gave extensive support in conducting the original GasLab research. I would also like to thank Ed Hazzard and Christopher Smick for extensive discussions of the GasLab models and of the ideas in this paper. Wally Feurzeig, Nora Sabelli, Ron Thornton and Paul Horwitz made valuable suggestions to the project design. Paul Deeds, Ed Hazzard, Rob Froemke, Ken Reisman and Daniel Cozza contributed to the design and implementation of the most recent GasLab models. Josh Mitteldorf has been an insightful critic of the subtle points of thermodynamics. Walter Stroup has been a frequent and invaluable collaborator throughout the GasLab project. Donna Woods gave unflagging support and valuable feedback on drafts of this chapter.
References
Buldyrev, S.V., Erickson, M.J., Garik, P., Shore, L. S., Stanley, H. E., Taylor, E. F., Trunfio, P.A.and Hickman, P. 1994. Science Research in the Classroom: The Physics Teacher 32, 411-415.
Chen, D., & Stroup, W. 1993. General Systems Theory: Toward a Conceptual Framework for Science and Technology Education for All. Journal for Science Education and Technology
Cutnell, J. & Johnson, K. 1995. Physics. New York: Wiley & Sons.
Daston, L. 1987. Rational individuals versus laws of society: from probability to statistics, Kruger, L. Daston, L. & Heidelberger, M. (Eds.), The Probabilistic Revolution, Vol. 1, MIT Press, Cambridge, MA.
Dawkins, R. 1976. The Selfish Gene. Oxford: Oxford University Press.
Dennett, D. 1995. Darwin’s Dangerous Idea: Evolution and the Meanings of Life. New York: Simon and Schuster.
diSessa, A. 1986. Artificial worlds and real experience, Instructional Science, 207-227.
Doerr, H. (1996). STELLA: Ten Years Later: A Review of the Literature. International Journal of Computers for Mathematical Learning. Vol. 1 no. 2.
Eisenberg, M. 1991. Programmable Applications: Interpreter Meets Interface. MIT AI Memo 1325. Cambridge, MA, AI Lab, MIT.
Feurzeig, W. 1989. A Visual Programming Environment for Mathematics Education'. Paper presented at the fourth international Conference for Logo and Mathematics Education. Jerusalem, Israel.
Forrester, J.W. 1968. Principles of Systems. Norwalk, CT: Productivity Press.
Gell-Mann, M. 1994. The Quark and the Jaguar. New York: W.H. Freeman
Giancoli, D. 1984. General Physics. Englewood Cliffs, NJ: Prentice Hall
Gigerenzer, G. 1987. Probabilistic Thinking and the Fight against Subjectivity, Kruger, L. Daston, L. & Heidelberger, M. (Eds.), The Probabilistic Revolution, Vol. 2, MIT Press, Cambridge, MA.
Ginsburg, H., & Opper, S. 1969. Piaget's Theory of Intellectual Development. Englewood Cliffs, NJ: Prentice-Hall.
Giodan, A. 1991. The importance of modeling in the teaching and popularization of science. Trends in Science Education, 41(4),
Gleick, J. 1987. Chaos. New York: Viking Penguin.
Hofstadter, D. (1979). Godel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books.
Holland, J. 1995. Hidden Order: How Adaptation Builds Complexity. Helix Books/Addison-Wesley.
Horwitz, P. 1989. ThinkerTools: Implications for science teaching. In J.D. Ellis (Ed.), 1988 AETS Yearbook: Information technology and Science Education (pp. 59-71).
Horwitz, P., Neumann, E., & Schwartz, J. 1994. The Genscope Project. Connections, 10-11.
Jackson, S., Stratford, S., Krajcik, J., & Soloway, E. 1996. A Learner-Centered Tool for Students Building Models. Communications of the ACM, 39 (4), 48-49.
Kauffman, S. 1995. At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford: Oxford University Press.
Kay, A. C. 1991. Computers, networks and education. Scientific American, 138-148.
Kelly, K. 1994. Out of Control. Reading, MA: Addison Wesley.
Kruger, L. Daston, L. & Heidelberger, M. (Eds.) 1987. The Probabilistic Revolution. Vol. 1, MIT Press, Cambridge, MA.
Langton, C. & Burkhardt, G. 1997. Swarm. Santa Fe Institute, Santa Fe: NM.
Lotka, A.J. 1925. Elements of Physical Biology. New York: Dover Publications.
Mandinach, E.B. & Cline, H.F. 1994. Classroom Dynamics: Implementing a Technology-Based Learning Environment. Hillsdale, NJ: Lawrence Erlbaum Associates
Mellar et al (1994). Learning With Artificial Worlds: Computer Based Modelling in the Curriculum. Falmer Press.
Minar, N., Burkhardt, G., Langton, C & Askenazi, M. 1997. The Swarm Simulation System: A Toolkit for Building Multi-agent Simulations. http://www.santafe.edu/projects/swarm/.
Minsky, M. 1987. The Society of Mind. Simon & Schuster Inc., New York
Nemirovsky, R. 1994. On ways of Symbolizing: the case of Laura and the Velocity Sign. Journal of Mathematical Behavior, 14, 4, 389-422.
Neuman, E., Feurzeig, W., Garik, P. & Horwitz, P. 1997. OOTLS. Paper presented at the European Logo Conference. Budapest: Hungary.
Noss, R. & Hoyles, C. 1996. The Visibility of Meanings: Modelling the Mathematics of Banking. International Journal of Computers for Mathematical Learning. Vol. 1 No. 1. pp. 3 - 31.
Ogborn, J. 1984. A Microcomputer Dynamic Modelling System. Physics education. Vol. 19 No. 3.
Papert, S. 1980. Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
Papert, S. 1991. Situating Constructionism. In I. Harel & S. Papert (Eds.) Constructionism (pp. 1 - 12). Norwood, NJ. Ablex Publishing Corp.
Papert, S. 1996. An Exploration in the Space of Mathematics Educations. International Journal of Computers for Mathematical Learning. Vol. 1 No. 1
Pea, R. 1985. Beyond amplification: Using the computer to reorganize mental functioning. Educational Psychologist, 20 (4), 167-182.
Prigogine, I., & Stengers, I. 1984. Order out of Chaos: Man’s New Dialogue with Nature. New York: Bantam Books.
Repenning, A. 1993. AgentSheets: A tool for building domain-oriented dynamic, visual environments. Ph.D. dissertation, Dept. of Computer Science, University of Colorado, Boulder.
Repenning, A. 1994. Programming substrates to create interactive learning environments. Interactive learning environments, 4 (1), 45-74.
Resnick, M. 1994. Turtles, Termites and Traffic Jams. Explorations in Massively Parallel Microworlds. Cambridge, MA: MIT Press.
Resnick, M., & Wilensky, U. 1998. Diving into Complexity: Developing Probabilistic Decentralized Thinking Through Role-Playing Activities. Journal of the Learning Sciences, 7 (2), 153-171.
Resnick, M. & Wilensky, U. 1995. New Thinking for New Sciences: Constructionist Approaches for Exploring Complexity. Presented at the annual conference of the American Educational Research Association, San Francisco, CA.
Richmond, B. & Peterson, S. 1990. Stella II. Hanover, NH: High Performance Systems, Inc.
Roberts, N. 1978. Teaching dynamic feedback systems thinking: an elementary view. Management Science, 24(8), 836-843.
Roberts, N. 1981. Introducing computer simulation into the high schools: an applied mathematics curriculum. Mathematics Teacher, pp. 647-652.
Roberts, N., Anderson, D., Deal, R., Garet, M., Shaffer, W. 1983. Introduction to Computer Simulations: A Systems Dynamics Modeling Approach. Reading, MA: Addison Wesley.
Roberts, N. & Barclay, T. 1988. Teaching model building to high school students: theory and reality. Journal of Computers in Mathematics and Science Teaching. Fall: 13 - 24.
Roetzheim, W. 1994. Entering the Complexity Lab. SAMS Publishing.
L. S. Shore, M. J. Erickson, P. Garik, P. Hickman, H. E. Stanley, E. F. Taylor, P. Trunfio, 1992. Learning Fractals by 'Doing Science': Applying Cognitive Apprenticeship Strategies to Curriculum Design and Instruction. Interactive Learning Environments 2, 205--226.
Smith, D. C., Cypher, A., & Spohrer, J. 1994. Kidsim: Programming agents without a programming language. Communications of the ACM, 37 (7), 55-67.
Starr, Paul. 1994. Seductions of Sim. The American Prospect, (17).
Thornton, R. & Sokoloff, D. 1990. Learning Motion concepts using real-time microcomputer-based laboratory tools. Am. J. of Physics, 58, 9
Tipler, P. 1992. Elementary Modern Physics. New York: Worth Publishers
Tversky, A. & Kahneman, D. 1974. Judgment Under Uncertainty: Heuristics and Biases. Science, 185, pp. 1124–1131.
Waldrop, M. 1992. Complexity: The emerging order at the edge of order and chaos. New York: Simon & Schuster.
White, B., & Frederiksen, J. 1998. Inquiry, Modeling, and Metacognition: Making Science Accessible to All Students. Cognition and Instruction, 16(1), 3-118.
Wilensky, U. & Resnick, M. in press. Thinking in Levels: A Dynamic Systems Approach to Making Sense of the World. Journal of Science Education and Technology. Vol. 8 No. 1.
Wilensky, U. 1997. What is Normal Anyway? Therapy for Epistemological Anxiety. Educational Studies in Mathematics. Special Edition on Computational Environments in Mathematics Education. Noss, R. (Ed.) 33 (2), 171-202
Wilensky, U. 1996. Modeling Rugby: Kick First, Generalize Later? International Journal of Computers for Mathematical Learning. Vol. 1, No. 1.
Wilensky, 1995-a. Paradox, Programming and Learning Probability: A Case Study in a Connected Mathematics Framework. Journal of Mathematical Behavior, 14 (2).
Wilensky, U. 1995-b. Learning Probability through Building Computational Models. Proceedings of the Nineteenth International Conference on the Psychology of Mathematics Education. Recife, Brazil, July 1995.
Wilensky, U. 1993. Connected Mathematics: Building Concrete Relationships with Mathematical Knowledge. Doctoral dissertation, Cambridge, MA: Media Laboratory, MIT.
Wilensky, U. 1991. Abstract Meditations on the Concrete and Concrete Implications for Mathematics Education. In I. Harel & S. Papert (Eds.) Constructionism. Norwood NJ: Ablex Publishing Corp.
Wright, W. 1992a. SimCity. Orinda, CA: Maxis.
Wright, W. 1992b. SimEarth. Orinda, CA: Maxis