levels

` levels

Thinking in Levels:
A Dynamic Systems Approach
to Making Sense of the World

Uri Wilensky
Mitchel Resnick

Journal of Science Education and Technology. Vol. 8 No. 1.

Abstract:
The concept of emergent "levels" (i.e. levels that arise from interactions of objects at lower levels) is fundamental to scientific theory. In this paper, we argue for an expanded role for this concept of "levels" in science education. We show that confusion of levels (and "slippage" between levels) as the source of many of people’s deep misunderstandings about patterns and phenomena in the world. These misunderstandings are evidenced not only in students’ difficulties in the formal study of science but also in their misconceptions about experiences in their everyday lives. The StarLogo modeling language is designed as a medium for students to build models of multi-leveled phenomena and through these constructions explore the concept of levels. We describe several case studies of students working in StarLogo. The cases illustrate students’ difficulties with the concept of levels, and how they can begin to develop richer understandings.

Introduction

Two high-school students were writing a computer program to simulate the flow of traffic on a highway. They began by writing some simple rules for each car: Each car would accelerate if it didn’t see any other cars ahead of it, and it would slow down if it saw another car close ahead. They started the program running, and observed the patterns of traffic flow. On the screen, a traffic jam formed. They continued to watch and–much to their surprise–the jam started drifting backward along the highway. "What’s going on?" said one of the students. "The cars are going forward, how can the jam be moving backward?"

This type of confusion is not unique to students modeling traffic jams. It arises in many different domains, among many different types of learners. At its core, it is a confusion of levels. By levels, we do not mean a classic hierarchy or chain of command, like the levels of officers in the army. Rather, we are talking about the levels of description that can be used to characterize a system with lots of interacting parts. This notion of levels is useful for understanding a wide range of phenomena in the world. Although we view the idea of levels as central to the study and practice of science, it is often missing in the discourse among scientists, and even less common in science classrooms or in the culture at large.

Why were the students surprised by the backward-moving jam? As we see it, the students viewed the jam as a simple collection of cars. If the cars are moving forward, the collection must do the same. But traffic jams are not simple collections of cars. For one thing, the constituent parts of the jam are constantly changing over time (cars move in and out of the jam). Moreover, the jam acts as an "object" in its own right, with its own rules of motion, different from the cars’ rules. True to the old saying, the whole is more (or, at least, different) than the sum of the parts.

In the study of science, these ideas commonly come to the surface when studying waves. In an ocean wave, it is the energy that moves, not the water molecules. Similarly, with a wave travelling along a rope: pieces of the rope move up and down, but the wave moves along the length of the rope. Traffic jams can be viewed as another type of wave, with density of cars analogous to the height of an ocean wave. In all of these waves, the motion of the wave is very different from the motion of the constituent parts.

These issues are confusing not only to high-school students. We showed the traffic program to two visiting computer scientists. They were not at all surprised that the traffic jams were moving backwards. They were well aware of that phenomenon. But then one of the researchers said: "You know, I've heard that's why there are so many accidents on the freeways in Los Angeles. The traffic jams are moving backwards and the cars are rushing forward, so there are lots of accidents." The other researcher thought for a moment, then replied: "Wait a minute. Cars crash into other cars, not into traffic jams." In short, he believed that the first researcher had confused levels, mixing cars and jams inappropriately. The two researchers then spent half an hour trying to sort out the problem. It is an indication of the underdeveloped state of notion of "levels" in our culture that two sophisticated computer scientists needed to spend half an hour trying to understand the behavior of a ten-line computer program written by high-school students.

In this paper, we argue for an expanded role for the concept of "levels" in the study of science. We view confusion of levels (and "slippage" between levels) as the source of many of people’s deep misunderstandings about patterns and phenomena in the world. These misunderstandings are evidenced not only in students’ difficulties in the formal study of science but also in their misconception about experiences in their everyday lives. Our goal is to help people develop better intuitions about levels–and a better sense of which levels are appropriate for which purposes. We believe that a better understanding of levels will enable people to construct causal explanations of a wide range of phenomena, and provide them with a framework that is useful across a wide range of disciplines. We see the concept of levels as a cornerstone to creating a more interdisciplinary approach to science–and, even more broadly, as a unifying concept to connect different domains of knowledge in the humanities and social sciences as well as the natural sciences.

An understanding of levels is becoming even more important with the increased presence of the computer in our culture. For one thing, people can use computers as tools for exploring the idea of levels–as in the case of the two high-school students simulating traffic patterns. Moreover, computers themselves are best understood by thinking in terms of levels. At one level, the operation of a computer program can be described in terms of movement of electrons; at another level, in terms of gates and transistors; at another level, in terms of assembly-language instructions; at yet another level, in terms of general algorithms and "intentions." Even more importantly, these computer-inspired ideas about levels are providing new metaphors and models for understanding many other complex systems in the world, offering a productive framework for thinking about some of the most difficult issues of science, from the evolution of species to the workings of the mind.

We live in an increasingly interconnected world. Economic actions in one country can instantly affect markets on the other side of the world. There are analogous ecological connections: smokestacks in one country can decimate rainforests on another continent. Traditionally, science has tended to study phenomena in isolation. Today, there is a greater need to develop systemic approaches for designing and understanding the world. A deep understanding of the concept of levels is crucial to developing such systemic approaches.

In the next section, we probe more deeply into the notion of levels. The rest of the paper revolves around three informal case studies of students and teachers exploring the concept of levels in the context of building computer-based models of complex systems. The studies are intended to probe how people think about levels, and to illustrate new tools and activities that can help people think about levels in new ways. Through these studies, we demonstrate the importance of "level thinking" for understanding a wide range of phenomena, and we suggest new pedagogical strategies for introducing these ideas to students.

What are Levels Anyway?: Leveling about Levels

People often talk about "levels" in everyday conversation, but they typically mean something quite different from the ideas that we are discussing in this paper. Indeed, "levels" can have many different meanings. In this section, we aim to distinguish between these different senses of levels, and we argue that these multiple interpretations contribute to people’s misunderstandings about levels.

Often, people think of levels in terms of hierarchies of control. In the army, the general is at the top level of the hierarchy, the private is at the bottom level, with sargents, lieutenants, and colonels in between. Commands flow down from higher levels to lower levels. Similarly, in most corporations, the chief executive is at the top level, then the president, then vice presidents, and so on. Modern management structures are moving away from strict hierarchies, but the traditional organization chart still dominates the way many people think about levels. So we call this approach to thinking about levels the "organization-chart view."

A very different meaning of levels, which we call the "container view," is based on the idea of parts and wholes. For example, we can view units of time in terms of levels. A day is a lower level than a week, which is a lower level than a month. The container view differs from the organization-chart view in that the lower-level elements are parts of the higher-level elements: A month is part of a year, but a sargent is not part of a general.

In this paper, we are focusing on yet another meaning of levels, which we call the "emergent view" of levels. Our focus is on levels that arise from interactions of objects at lower levels–like the traffic jam that emerged from the interactions among the cars. These levels might seem similar to the part/whole levels: just as a year is made up of months, traffic jams are made up of cars. But the jam/car relationship is different in some very important ways. For one thing, the composition of the jam keeps changing; some cars leave the jam and other cars enter it. Moreover, the jam arises from interactions among the cars; it is not just a simple accumulation of cars. Months do not interact to form a year; they simply accumulate or "add up."¹ A year can be viewed, essentially, as a long month. But a traffic jam is not just a big car. It is qualitatively different. And that is what led to the high-school students’ surprise: the jam behaved very differently from the cars, moving backwards while the cars within it moved forward.

Many systems in the world work somewhat like traffic jams. Once sensitized to these ideas, we see "jams" wherever we look. We continue to recognize our friends, even though their cells are constantly entering and leaving the "jams" of their bodies. Similarly, we continue to identify companies, countries, and other organizations even though the people within them are constantly changing over time. From this perspective, we can think of the levels within a corporate organization in a new way. Rather than focusing on CEOs, managers, and assembly-line workers within a hierarchy (as in the organization-chart view), we can think about corporate divisions and the employees within them. As any good manager can tell you, the performance of a corporate division is not a simple combination of the actions of the employees within it (nor a direct result of the person in charge); rather, it depends on the complex web of relationships and interactions among all of the employees.²

This notion of levels is central to understanding the emerging "sciences of complexity"–the investigation of how complex phenomena can arise from simple components and simple interactions. New research projects on chaos, self-organization, adaptive systems, nonlinear dynamics, and artificial life are all part of this growing interest in complex systems. The interest has spread from the scientific community to popular culture, with the publication of general-interest books about research into complex systems (e.g., Gleick, 1987; Waldrop, 1992; Gell-Mann, 1994; Kelly, 1994; Roetzheim, 1994; Holland, 1995; Kauffman, 1995).

Research into complex systems touches on some of the deepest issues in science and philosophy–order vs. chaos, randomness vs. determinacy, analysis vs. synthesis. In the minds of many, the study of complexity is not just a new science, but a new way of thinking about all science, a fundamental shift from the paradigms that have dominated scientific thinking for the past 300 years. Although complexity researchers have not focused extensively on the notion of levels, we view levels as one of the central ideas of the sciences of complexity–and especially important in helping nonexperts gain an understanding of the sciences of complexity. By foregrounding the notion of levels, we hope to enable people to transform their view of systems, using levels as a framework for seeing systems from multiple perspectives. We expect that this transformation will enable people to develop better causal accounts of the interactions and relationships among elements of the systems they encounter.

Indeed, the notion of levels is a powerful tool for understanding some of the most long-standing issues in science. Some of the greatest controversies and advances in the field of evolutionary biology hinge on a question of levels–for example, is it appropriate to think about variation and selection at the level of the gene or the organism or the species (Dawkins, 1976; Dennett, 1995; Williams, ??)? Similarly, many current investigations into the nature of mind focus on the idea of levels. Minsky (1987) argues that mind arises from the interactions among a complex society of agents that organize themselves into a variety of structures. Hofstadter (1979) compares the mind to an ant colony; just as the behavior of a colony arises from interactions of individual ants, mind arises from the interactions among "cognitive ants."

There is no doubt that people have difficulty understanding this emergent sense of levels (Resnick, 1994; Wilensky, 1995b). But there are reasons to be optimistic about the possibilities for helping people overcome their confusions about levels. There are some indications that people can become engaged with the notion of emergent levels–much more than they would with other difficult concept. In our own research in participatory simulations (Resnick & Wilensky, 1997), we have engaged people of all ages in playful explorations of multi-level thinking. On a broader scale, many people have experienced the idea of emergent levels directly by participating in "human waves" at sports stadiums. Individual people simply stand up and sit down, but the wave moves around the stadium. Why has this activity become so popular? Despite (or, perhaps, because of) the deep confusion that is associated with the notion of levels, people seem to take particular delight in "playing with" the idea of levels. There is something almost magical in the way behaviors at one level arise out of very different behaviors at another level.

Leveling Stories

In this section, we explore the notion of emergent levels through a set of case studies or "stories," illustrating how people have difficulty with this concept, and how they can begin to develop richer understandings. These stories draw largely on experiences with StarLogo ³(Resnick, 1994; Wilensky, 1995), a computer modeling environment designed explicitly for exploring systems with multiple interacting objects. StarLogo is an extension of the computer language Logo, and builds on the Logo metaphor of a "turtle." In traditional Logo, students create graphic images by giving commands to the turtle. In StarLogo, students can give commands to hundreds or thousands of turtles, telling the turtles how they should move and interact with one another. In StarLogo, turtles are not necessarily turtles any more–students can use StarLogo turtles to represent all different types of "agents," such as cars in a traffic jam or molecules in a gas.

StarLogo users can also program the behavior of the environment in which the turtles live. The environment is represented as a grid of small squares called "patches." For example, a patch might represent a piece of the road in the traffic simulation, and it would keep track of information such as the amount of oil spilled on the road. Like the turtles, the patches are "computationally active": students can write rules for the patches (for example, telling the patches what to do if a car passes by). In computer-science terms, StarLogo can be viewed as a collection of agents moving on top of (and interacting with) a two-dimensional cellular automata.

We have used StarLogo as a platform for supporting student explorations (and studying student thinking) in several settings, generally at secondary schools and universities. There are two general ways in which we engage students in using StarLogo. In some cases, students use StarLogo to build models "from scratch"–that is, they choose phenomena of interest to them (such as the formation of traffic jams) and write StarLogo programs to model (and explore the workings of) the phenomena. In other cases, we introduce a pre-built StarLogo model and engage students in discussing the workings of the model–and then invite them to modify or extend the model to deepen their understanding of it. In all cases, we work closely with individual students to gain a deeper understanding of how students think about complex phenomena–and how their thinking evolves as they build and explore models of such phenomena.

Below, we present three case studies of student experiences with StarLogo. The cases examine how students developed an understanding of emergent levels, and how this understanding helped them gain insight into the phenomena they were investigating. Each story focuses on a different scientific domain and each highlights a different theme. The first, focusing on the behavior of slime-mold cells, introduces the basic scientific and philosophical issues related to levels. The second, focusing on the behavior of gas particles in a box, discusses the pedagogical benefits of introducing the concept of levels into science education. The third, focusing on the behavior of simple predator-prey ecosystems, analyzes how different computer-based modeling tools influence the ways students think about levels.

Slime⁴

We have found that thinking about the life cycle of slime mold is an effective entry point for introducing students to the concept of levels. Slime mold is hardly the most glamorous of creatures, but it is surely one of the most strange and intriguing. As long as food is plentiful, slime-mold cells exist independently as tiny amoebas. They move around, feed on bacteria in the environment, and reproduce simply by dividing into two. But when food becomes scarce, the slime-mold behavior changes dramatically. The slime-mold cells stop reproducing and move towards one another, forming a cluster (called a "pseudoplasmodium") with tens of thousands of cells.

At this point, the slime-mold cells start acting as a unified whole. Rather than lots of unicellular creatures, they act as a single multicellular creature. It changes shape and begins crawling, seeking a more favorable environment. When it finds a spot to its liking, it differentiates into a stalk supporting a round mass of spores. These spores ultimately detach and spread throughout the new environment, starting a new cycle as a collection of slime-mold cells. (See figure 1, reproduced from Prigogine and Stengers (1984)).

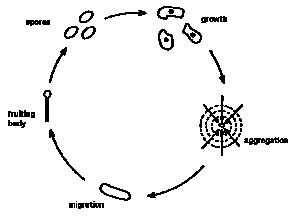
Figure 1
Slime Mold Cycle

To engage students in exploring the behavior of slime mold–and, more broadly, exploring the nature of levels–we wrote a StarLogo program that models the slime-mold aggregation process. We were not interested in simulating every detail of the actual slime-mold mechanism. Our goal was to capture the essence of the aggregation process with the simplest mechanism possible. Our StarLogo program is based on a set of simple rules. Each turtle is controlled by four rules: one makes the turtle move, a second adds a little randomness to the turtle’s movements, a third makes the turtle emit a chemical pheromone, and a fourth makes the turtle "sniff" for the pheromone and turn in the direction where the chemical is strongest (that is, follow the gradient of the pheromone). Meanwhile, each patch is controlled by two rules: one to make the pheromone in the patch evaporate, and another to diffuse the pheromone to neighboring patches. Each rule is very simple, requiring at most two lines of StarLogo code.

If we start the simulation with a small number of turtles, not much happens. We see faint green trails of pheromone behind each turtle. But these trails quickly dim as the pheromone evaporates and diffuses. Sometimes a turtle will follow another turtle for a short while, but it quickly loses the trail. Overall, the screen has a faint green aura, indicating a low level of pheromone everywhere, but no bright green areas. The turtles seem to wander aimlessly, looking somewhat like molecules in a gas.

But if we add enough turtles to the simulation, the behavior changes dramatically. With lots of turtles, there is a better chance that a few turtles will wander near one another. When that happens, the turtles collectively drop a fair amount of pheromone, creating a sort of pheromone "puddle" (shown as a bright green blob on the display). The turtles in the puddle, by following the pheromone gradient, are likely to stay within the puddle–and drop even more pheromone there, making the puddle even bigger and more "powerful." And as the puddle expands, more turtles are likely to "sense" it and seek it out–and drop even more pheromone. The result is a self-reinforcing positive feedback loop: (1) the more pheromone in the puddle, the more turtles it attracts, and (2) the more turtles attracted to the puddle, the more pheromone they drop in the puddle.

With enough turtles, this same process can play out in many locations, resulting in turtle/pheromone clusters all over the computer screen. Through the positive-feedback mechanism, the clusters tend to grow larger and larger (figure 2). What’s to stop the clusters from growing forever? The positive-feedback loop is balanced by a negative-feedback process: as the clusters become bigger, there are fewer "free" turtles wandering around the world, depriving the positive-feedback process of one of the "raw materials" that it needs to keep going. For the clusters to keep growing, the system would need a never-ending supply of new turtles.


t = 0	t = 20	t = 40	t = 60


t = 80	t = 200	t = 500

Figure 2: 500 iterations with 1000 slime-mold cells

As students have experimented with this model (adjusting parameters such as number of turtles and pheromone evaporation rate, and in some cases adding new features to the model), we have observed their engagement with several important issues related to the concept of levels:

What is an object?

The life cycle of slime mold touches on one of the most fundamental issues that arises when thinking about levels: What is an object anyway? Or, in other words, when is something a "thing"? Is the slime mold a society of thousands of separate objects that sometimes cooperate? Or is it a single object that divides into separate pieces under certain conditions? In short, should we refer to slime mold as "it" or "they"?

Languages make a fundamental distinction between the singular and the plural. Indeed, in writing the above description, we needed to decide whether to use the verb "is" or "are" when referring to slime mold. But, as the case of the slime mold shows, the distinction between singular and plural is not as sharp as might first appear. As mentioned earlier, leading cognitive-science researchers, such as Papert and Minsky (1987), have proposed models of mind (and self) as composed of societies of interacting entities. In each of our lives, one of our most fundamental realities is the experience of ourselves (and our selves) as singular entities. Our language, typified by the use of the singular pronoun "I," reflects (and, perhaps, reinforces) this view. But the new distributed models of mind require a new stance in thinking about the "self" as sometimes an "I" and sometimes a "we." Similarly, new ecological models encourage us to sometimes view ecosystems as a collection of interacting organisms, but sometimes as an integrated whole (Lovelock, 1979).

In our view, the very question of "objectness" becomes a question of "levels." Objects that are viewed as singular at one level are best viewed as plural at another level. The ability to shift levels, viewing the same object as either singular or plural, depending on the situation, is a prerequisite for building deep, scientific understandings of phenomena. There is no "right answer" to the question of whether slime mold is (are?) singular or plural. Whether it is best to think about slime mold as singular or plural depends on what question you are trying to answer–and which stance (that is, which level of description) provides a better explanatory account of the question.

Emergent objects

When students began experimenting with our StarLogo slime-mold model, many of them did think in terms of levels–but in the organization-chart sense. When we asked students how they might program the slime-mold cells to aggregate into clusters, most of the students immediately responded that they would put one of the slime-mold cells in charge, and it would "give orders" to the other cells, instructing them where to go.

It’s not surprising that students had this organization-chart perspective. In fact, the process through which slime-mold cells aggregate into a single multicellular creature has been a subject of scientific debate (Keller, 1983). For many years, scientists believed that the aggregation process was coordinated by specialized slime-mold cells, known as "founder" or "pacemaker" cells (which act somewhat like chief executives in an organization). According to this theory, each pacemaker cell sends out a chemical signal, telling other slime-mold cells to gather around it, resulting in a cluster. In 1970, Keller and Segel (1970) proposed an alternative model, showing how slime-mold cells can aggregate without any specialized cells. Nevertheless, for the following decade, other researchers continued to assume that special pacemaker cells were required to initiate the aggregation process. As Keller (1985) writes, with an air of disbelief: "The pacemaker view was embraced with a degree of enthusiasm that suggests that this question was in some sense foreclosed." It wasn’t until the early 1980’s, based on further research by Cohen and Hagan (1981), that researchers began to accept the idea of aggregation among homogeneous cells, without any pacemaker.

The decade-long resistance serves as some indication of the strength of what we call the "centralized mindset" (Resnick, 1994). When people see patterns in the world, then tend to assume centralized control, even if it doesn’t exist. And when people try to create structures in the world (such as organizations or technological artifacts), they often impose centralized control even if it is not needed. People have difficulty recognizing that objects (such as slime-mold clusters) can arise from simple, decentralized interactions, rather than centralized, top-down control. So as students worked on the StarLogo model, it seemed "natural" for them to put one of the slime-mold cells in charge, putting the rest of the cells lower down in the "organizational chart."

Mechanisms of emergence

Even when students began thinking of the StarLogo model in more decentralized ways, they tended to assume that each individual slime-mold cell should follow an explicit, deterministic set of instructions. But, in fact, the cells in our StarLogo program have a bit of randomness in their motion. This randomness serves one obvious purpose: it ensures that "free" turtles will eventually wander near some cluster. Once a free turtle wanders near a cluster, it senses the pheromone from the cluster, and begins to follow the gradient of the pheromone. At that point, the randomness might seem to play a negative role. Why would we want to cripple a turtle’s ability to follow the pheromone?

In fact, the program would be quite boring if the turtles followed the pheromone perfectly. Eventually, each turtle would join a cluster. After that, not much more would happen. Individual clusters could never grow larger or smaller, and the number of clusters would never change. Although turtles would still move around within their clusters, the composition of each cluster would be fixed. Turtles would never leave their clusters. The screen would be filled with stable, unchanging green blobs (with a little activity inside each blob).

A bit of randomness in the turtles’ movements leads to a much different dynamic. Turtles are not forever "bound" to the clusters they join. Sometimes, through its random motion, a turtle will break free of its cluster and begin wandering again. Such an escape can initiate a ripple effect. With one fewer turtle in the cluster, there is a little less pheromone in the cluster. So the cluster is a little less likely to attract new turtles, and a little more likely to lose some of its remaining turtles. If another turtle escapes, the cluster becomes even weaker, and even less likely to hold onto its remaining turtles. As a result, small clusters often break apart suddenly. One turtle escapes, and then another, and another, in rapid succession. Underlying this rapid disintegration is the same positive-feedback process that drives the formation of clusters–but operating in the reverse direction.

So as the program proceeds, small clusters are likely to break apart, freeing turtles to join (and enlarge) the remaining clusters. As a result, the number of clusters tends to decline with time, and the number of turtles in each cluster tends to increase. As the clusters grow larger and larger, they become more and more stable. Turtles are less likely to escape. And even when an errant turtle escapes, it is less likely to set off a chain reaction destroying the entire cluster.

At first, students had great difficulty understanding the value of randomness in the model. They saw randomness as something that destroys order and interferes with goals. They seemed to have a "deterministic mindset" (Wilensky, 1997)–in the spirit of Einstein’s famous, erroneous proclamation that "God doesn’t play dice." Indeed, scientists over the past three centuries have struggled to accept and understand the role and value of probabilistic processes. It is not surprising that students working on StarLogo models experience the same struggles. However, as long as students hold tightly to the deterministic mindset, they will never develop a complete understanding of "emergent levels," since they will miss the key role that randomness plays in the mechanisms of emergence.

We believe that one of the underlying causes of the deterministic mindset is a type of "level confusion." Students have a difficult time believing that randomness on one level (the cells) could lead to a desired behavior on another level (the formation of clusters). This was only one of many level confusions that we observed in student interactions with StarLogo models. Indeed, level confusions seem to be a fundamental obstacle to the understanding of a wide range of phenomena in nature and society.

An example of a level confusion arose as students experimented with different "senses of smell" for the slime-mold cells. Some students tried to change the range of directions that the turtles sniff. By default, each turtle takes three sniffs in trying to follow the gradient of a scent: one sniff straight ahead, one sniff 45 degrees to the left of its heading, one sniff 45 degrees to the right of its heading. (On each sniff, the turtle senses one unit-distance away from its current position.) What if we make the turtles take more sniffs? Say each turtle takes five sniffs: 90 degrees to the left, 45 degrees to the left, straight ahead, 45 degrees to the right, and 90 degrees to the right. Equivalently, we could think of this as increasing the number of noses on each turtle, so that each turtle has five noses instead of three noses, equally spaced at 45 degree intervals. With five noses/sniffs rather than three, the turtles clearly have a better sense of smell. How will this improved sense of smell change the dynamics of the program? Will there be more clusters or fewer? Will the clusters be larger or smaller?

We posed this scenario to about two dozen people (including high-school students and MIT researchers). Interestingly, more than three-quarters of the people predicted the result incorrectly. Most people expected fewer and bigger clusters. In fact, the turtles gather into more and smaller clusters. It isn’t too surprising that many people had difficulty predicting what would happen. After all, the slime mold program involves thousands of interacting objects. It is very difficult to make predictions about such complex systems. So it wouldn’t be too surprising if half of the people predicted the result incorrectly. But it seems strange that most people predicted incorrectly. What underlies this false intuition?

We asked people to explain their reasoning. Many people reasoned something like this: "The creatures are trying to get together, to combine into one big thing. If the creatures have a better sense of smell, they will do a better job of that. So you’ll end up with larger clusters." What’s the flaw? This reasoning confuses levels and attributes inappropriate intentionality to the creatures. Creatures are not really trying to form large clusters; they are simply following a pheromone gradient. The creatures do follow the gradient more effectively when they have more noses. But as a result, they form smaller (not larger) clusters. By following the gradient effectively, the many-nosed creatures more quickly "find" other creatures to interact with. Giving more noses to the creatures is like giving a larger cross-section to particles in a physics simulation: collisions are more likely. And once the creatures find some others to interact with, they can form stable clusters with fewer partners, since each creature in the cluster stays closer to the others. The result: clusters are smaller, there are more of them, and they form more quickly.

Gas in a Box⁵

This story focuses on how certain computational models can help students (and teachers) make connections between levels that aren’t readily apparent. It is a story about Harry, a science and mathematics teacher in the Boston public schools, who was very interested in the behavior of gases. He remembered from school that the energies of the particles in a gas form a stable distribution called a Maxwell-Boltzman distribution (see figure 3). Yet, he didn’t have any intuitive sense of why they might form this stable asymmetric distribution. Why should this pattern be common to all gases? Does it depend on initial conditions? On the types of particles? If you start with all of the particles exactly the same, would they stay that way or would they "spread apart" into this distribution? And why was the distribution asymmetric? If all of the particles are essentially the same, why should the distribution be asymmetric?

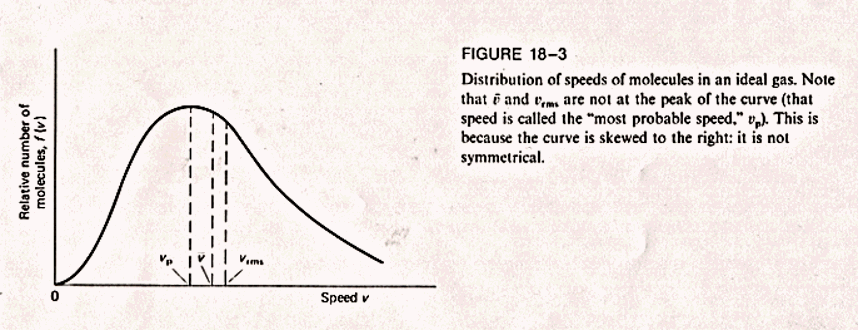
Figure 3: Maxwell-Boltzman Distribution (illustrration from Giancoli, 1984)

To explore these questions, Harry decided to use StarLogo to build a model of gas particles in a box. Harry’s model displays a box with a specified number of gas particles randomly distributed inside it. The user can set various parameters for the particles: mass, speed, direction. The user can then perform "experiments" with the particles. Harry wrote a program to model the standard Newtonian physics of particles colliding with one another and with the sides of the box. As in the classical models of an ideal gas, he modeled the collisions as "elastic"–that is, no energy is "lost" during collisions.

Harry called his program GPCEE (for Gas Particle Collision Exploration Environment), though other students have subsequently dubbed it "GasLab" (Wilensky, in press). Harry’s program was a relatively straightforward StarLogo program. At its core were three procedures which were executed (in parallel) by each of the particles in the box:

go: the particle checked for obstacles and, if none were present, moved forward (an amount based on its speed variable) for one clock tick;

bounce: if the particle detected a wall of the box, it would bounce off the wall

collide: if the particle detected another particle in its vicinity, they would bounce off of each other like billiard balls.

Harry was excited by the fact that the laws of the gas should emerge, automatically, from the simple rules he had written for the particles. He realized that he wouldn’t need to program the macro-level gas rules explicitly; they would come "for free" if he wrote the underlying (micro-level) particle rules correctly. He hoped to gain further confidence in the gas laws through this approach – seeing them as the emergent result of the laws of individual particles and not as some mysterious orchestrated properties of the gas.

In one of his experiments, Harry created a collection of particles of equal mass, then initialized them to start at the same speed but moving in random directions. He wrote a program to monitor the average speed of the particles. He was surprised to find that the average speed decreased over time. He knew that the overall energy of the system should be constant: energy was conserved in each of the collisions. But energy is proportional to the mass and to the square of the velocity. The masses were constant and the overall energy was constant. So shouldn’t the average speed be constant?

At first, he assumed there was a bug in his computer program, but he couldn’t find the bug. To try to get a better understanding of what was going on, he decided to color-code the particles according to their speed: particles are initially colored green; as they speed up, they get colored red; as they slow done, they get colored blue. Soon after starting the model running, Harry observed that there were many more blue particles than red particles. This color distribution gave him a concrete way of thinking about the asymmetric Maxwell-Boltzman distribution. He could "see" the distribution: initially all the particles were green, a unform symmetric distribution, but as the model developed, there were increasingly more blue particles than red ones, resulting in a skewed asymmetric spread of the distribution.

Figure 4
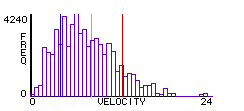
8000 gas particles after 30 ticks. Faster molecules are red, slower molecules blue and average molecules are green.

Figure 5
Dynamic histogram of molecule speeds after 30 clock ticks.

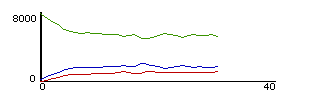
Figure 6
Dynamic plot of numbers of fast, slow and medium speed particles

As Harry played with the model, he also gained a way of thinking about the average-speed problem. If there are more slow (blue) particles than fast (red) ones, then the average speed would indeed have to drop – so this wasn’t necessarily a bug in the program.

Even though Harry knew about the asymmetric Maxwell-Boltzman distribution, he was surprised to see the distribution emerge from the simple rules he had programmed. But, since he had programmed the rules, he gained greater faith that this stable distributiion does indeed emerge. Harry tried several different initial conditions and all of them resulted in this distribution. He now believed that this distribution was not the result of a specific set of initial conditions, but that any gas, no matter how the particles speeds were initialized, would attain this stable distribution. In this way, the StarLogo model served as an experimental lab where the distribution could be "discovered." This type of experimental lab is not easily (if at all) reproducible outside of the computer-modeling envirtonment.

But there remained several puzzles for Harry. Though he believed that the Maxwell-Boltzman distribution emerged from his rules, he still did not see why they emerged. And he still did not understand how these observations squared with his mathematical knowledge – how could the average speed change when the average energy was constant? Harry found several solutions. Although there were many fewer red particles than blue ones, Harry realized that each red particle "stole" a significant amount of energy from the constant overall pool of energy. The reason: energy is proportional to the square of speed, and the red particles were high speed. So each red particle need to be "balanced" by more than one blue particle to keep the overall energy constant. From a more classical mathematical perspective, he realized the energy for the overall gas would remain constant if and only if the sum of the squares of the particle speeds remained constant. By using standard algebra, he worked out that this result was not the same as the sums of the speeds themselves remaining constant.

The above reasoning relieved Harry’s worries about how such an asymmetric ensemble could be stable. But there remained the question – why would the particle speeds spread out from their initial uniform speed? To think about this question, Harry turned to the micro-level – what happens when two particles collide? Harry experimented with various angles for collisions between particles and observed that the average speed did not usually stay constant. Indeed, it remained only constant when the particles collided head-on. The apparent symmetry of the situation was broken when the particles did not collide head-on – that is, when their velocities they did not have the same relative angle to the line that connected their centers. Harry went on to do the standard physics calculations that confirmed this experimental result. In a one-dimensional wrold, he concluded, average speed would stay constant; in a multi-dimensional world, particle distribtuions become non-uniform and this leads to an asymmetric distibution.

Harry’s story highlights the importance of "level-headed" thinking – that is, understanding phenomena through a framework of levels. In his reasoning, Harry constantly shifted between levels. His approach was not simply "reductionist" – that is, he did not merely try to explain the macro-behavior in terms of the micro-rules, but developed explanations that flowed back and forth between the levels. He began to understand the Maxwell-Boltzman distribution based on his micro-analysis of two particles colliding. But at the same time, he gained deeper understanding the drop of average speed in the collision of the two particles by appealing to energy considerations of the ensemble – namely, high-speed particles steal too much energy from the ensemble (since energy is proportional to the square of the velocity) so they must be balanced by many more low-speed particles. Harry needed to understand both of these levels (and the interactions between them) in order to develop a deeper understanding of the Maxwell-Boltzman distribution.

Indeed, it is difficult to make any good sense of the notion of distribution without thinking in terms of levels. A distribution is a macro-level description of what emerges from micro-level interactions. We see this characterization of distribution as fundamental – but one that is generally overlooked in classroom presentation, where the micro-level may be quickly mentioned, but all the attention is focused on the macro properties of distributions (e.g., mean, variance, standard deviation...).

A dsitribution can be seen as a new form of emergent object. In the slime mold example, the emergent object was spatial – that is, a spatial agglomeration of slime cells. In other words, there was a detectable pattern in the x-y position of the slime cells. In the gas particle example, the pattern is not in x-y positions of the particles, but in another parameter, the speeds of the particles. Because speeds unfold over time, this pattern is more difficult to detect, resulting in a less perceptually-obvious emergent object. Yet, fundamentally, the speed distribution and the slime-mold clusters are in the same category – emergent objects. By color-coding the particles, Harry made this speed distribution pattern more perceptible; the asymmety of the color distribution leaped out from the screen. Harry went further and used StarLogo to create a dynamic histogram of particle speeds – this enabled him to see the Maxwell-Boltzman distribution unfold over time.

Many other students and teachers have subsequently used and extended Harry’s original GasLab model. For example, several students added a piston to the box and designed a simulated pressure-meter (or barometer). They were thus able to vary the volume of the box and see the effect on the pressure of the gas. Other students split the box into two chambers and then allowed two separate gases to mix. Yet another group designed a virtual heater that heated and cooled the gas, then measured the effects on pressure, energy, and mean free path of the particles.

In all of these experiments, students needed to develop a richer conception of macro-quantities such as pressure. Typically, pressure is taught in high-school science classes as a "black box." Students learn how pressure relates to other macro-quantities (such as volume and temperature) via "gas laws." But they never learn the "mechanisms" underlying pressure. They use instruments to measure pressure, but never need to know how the instruments work. In working on their StarLogo gas models, students needed to go inside the black box – they had to understand how pressure emerged from individual particle interactions. The students made several tries at constructing a measure of pressure; they finally decided on having the sides of the box store the momentum from collisions with the particles. The momentum transferred to the box was their measure of pressure.⁶

In all of these explorations, students were best able to develop a deeper understanding of the phenomena when they made connection between the micro- and macro- levels of the phenomena – that is, when they connected properties of the gas with properties and interactions of the individual particles. Unfortunately, most school curricula deal with macro- and micro- phenomena in separate classes and subjects. In the GasLab case, the collisions of individual particles or billiard balls are typically handled in an introductory physics class, while the properties of the gas as a whole are studied in chemistry. Without good modeling tools, it is indeed difficult to treat these two domains together – the mathematical apparatus for connecting them is developed in graduate classes in statistical mechanics. Yet, when students are deprived of these connections, they are denied access to the mechanisms that truly explain the macro-level pheonemena that they observe in the world. The StarLogo modeling language enables much younger and less mathematically knowledgeable students to have access to explanations that connect the micro- and macro- levels of phenomena.

Predator-Prey⁷

The way that we see the world is greatly ingfluenced by the tools that we have at our disposal. In this story, we describe the use of StarLogo to make sense of the dynamics of predatory-prey interactions – and discuss how other tools, by focusing on different levels of the interaction, would lead to different ways of thinking about these phenomena.

Benjamin, a student at a Boston-area high school, set out to create a StarLogo program that would simulate the dynamics of an ecosystem. At the core of his simulation were turtles and food. His basic idea was simple: turtles that eat a lot of food reproduce, and turtles that don’t eat enough food die. Benjamin began by making food grow randomly throughout the StarLogo world. (During each time step, each StarLogo patch had a random chance of growing some food.) Then he created some turtles. The turtles had very meager sensory capabilities. They could not "see" or "smell" food at a distance. They could sense food only when they bumped directly into it. So the turtles followed a very simple strategy: Wander around randomly, eating whatever food you bump into.

Benjamin gave each turtle an "energy" variable. Every time a turtle took a step, its energy decreased a bit. Every time it ate some food, its energy increased. Then Benjamin added one more rule: if a turtle’s energy dipped to zero, the turtle died. With this program, the turtles do not reproduce. Life is a one-way street: turtles die, but no new turtles are born. Still, even with this simple-minded program, Benjamin found some surprising and interesting behaviors.

Benjamin ran the program with 300 turtles. But the environment could not support that many turtles. There wasn’t enough food. So some turtles began to die. The turtle population fell rapidly at first, then it levelled out at about 150 turtles. The system seemed to reach a steady state with 150 turtles: the number of turtles and the density of food both remained roughly constant.

Then Benjamin tried the same program with 1000 turtles. If there wasn’t enough food for 300 turtles, there certainly wouldn’t be enough for 1000 turtles. So Benjamin wasn’t surprised when the turtle population began to fall. But he was surprised with how far the population fell. After a while, only 28 turtles remained. Benjamin was puzzled: "We started with more, why should we end up with less?" After some discussion, he realized what had happened. With so many turtles, the food shortage was even more critical than before. The result: mass starvation. Benjamin still found the behavior a bit strange: "The turtles have less (initial energy as a group), and less usually isn’t more."

Next, Benjamin decided to add reproduction to his model. His plan: whenever a turtle’s energy increases above a certain threshold, the turtle should "clone" itself, and split its energy with its new twin. That can be accomplished by adding another parallel process to the program.

Benjamin assumed that the rule for cloning would somehow "balance" the rule for dying, leading to some sort of "equilibrium." He explained: "Hopefully, it will balance itself out somehow. I mean it will. It will have to. But I don’t know what number it will balance out at." After a little more thought, Benjamin suggested that the food supply might fall at first, but then it would rise back and become steady: "The food will go down, a lot of them will die, the food will go up, and it will balance out."

Benjamin started the program running. As Benjamin expected, the food supply initially went down and then went up. But it didn’t "balance out" as Benjamin had predicted: it went down and up again, and again, and again. Meanwhile, the turtle population also oscillated, but out of phase with the food.

On each cycle, the turtles "overgrazed" the food supply, leading to a scarcity of food, and many of the turtles died. But then, with fewer turtles left to eat the food, the food became more dense. The few surviving turtles thus found a plentiful food supply, and each of them rapidly increased its energy. When a turtle’s energy surpassed a certain threshold, it cloned, increasing the turtle population. But as the population grew too high, food again became scarce, and the cycle started again.

Visually, the oscillations were striking. Red objects (turtles) and green objects (food) were always intermixed, but the density of each continually changed. Initially, the screen was dominated by red turtles, with a sparse scattering of green food. As the density of red objects declined, the green objects proliferated, and the screen was soon overwhelmingly green. Then the process reversed: the density of red increased, with the density of green declined.

Many other students have worked on similar predator-prey models. Another student, Gabrielle, worked on a similar model using wolves and sheep rather than turtles and food. She was curious whether the nature of the predator-prey oscillations might depend on the parameters of the StarLogo program. She wondered what would happen if she started the simulation with a very large number of sheep? She guessed that the sheep would then dominate the ecosystem.

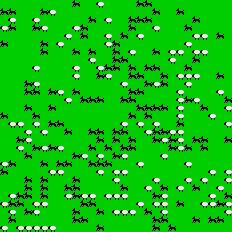
Figure 7
Wolves and Sheep

When Gabrielle ran the program, she was in for a surprise: all of the sheep died. At first she was perplexed: she had started out with more sheep and ended up with less. We have seen many students become emotionally involved with the fate of the "creatures" in their simulations – even when the creatures are represented as mere dots of light on their computer screen. Often, when they see the creatures endangered by the trough of an oscillation, they attempt to add more of the endangered creature to ensure its survival. But, in this case, Gabrielle’s attempt to help the sheep had exactly the oppposite effect. Some students devise an explanation for this seemingly paradoxical result. They realize that the "trough" of the oscillation must drop below zero. And once the population drops below zero, it can never recover. There is no peak after a negative trough. Extinction is forever: it is a "trapped state."

Gabrielle’s initial reponse is an indication of a classic level confusion: she tried to achieve a group-level result by focusing only on the individuals – without considering the intereactions among them. It is as if Gabrielle assumed that each sheep had a particular chance of survival, and then added more sheep to increase the chances of a large group surviving. In this way of thinking, the chances just add up. But in fact, there is a feedback mechanism in the system, so that increased numbers result in reduced chances (that, in fact, more than compensate for the increase in numbers).

The oscillating behavior in Benjamin’s and Gabrielle’s models is characteristic of all types of predator-prey systems. Traditionally, scientific (and educational) explorations of predator-prey systems are based on sets of differential equations, known as the Lotka-Volterra equations (Lotka 1925; Volterra 1926). For example, the changes in the population density of the prey (n1) and the population density of the predator (n2) can be described with the following differential equations:

dn1/dt = n1(b - k1n2)

dn2/dt = n2(k2n1 - d)

where b is the birth rate of the prey, d is the death rate of the predators, and k1 and k2 are constants. It is straightforward to write a computer program based on the Lotka-Volterra equations, computing how the population densities of the predator and prey vary with time (e.g., Roberts et al., 1983).

This differential-equation approach is typical of the way that scientists have traditionally modeled and studied the behaviors of a wide range of dynamic systems (physical, biological, and social). Scientists typically write down sets of differential equations then attempt to solve them either analytically or numerically. These approaches require advanced mathematical training; usually, they are studied only at the university level.

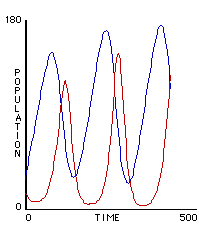
Figure 8
Oscillation in wolf (red) and sheep (blue) population

The StarLogo approach to modeling systems (exemplified by Benjamin’s and Gabrielle’s predator-prey projects) is sharply different. StarLogo makes systems-related ideas much more accessible to younger students by providing them with a stronger personal connection to the underlying models. Traditional differential-equation approaches are "impersonal" in two ways. The first is obvious: they rely on abstract symbol manipulation (accessible only to students with advanced mathematical training). The second is more subtle: differential equations deal in aggregate quantities. In the Lotka-Volterra system, for example, the differential equations describe how the overall populations (not the individual creatures) evolve over time. There are now some very good computer modeling tools–such as Stella (Roberts et al., 1983) and Model-It (Jackson et al., 1996)–based on differential equations. These tools eliminate the need to manipulate symbols, focusing on more qualitative and graphical descriptions. But they still rely on aggregate quantities.

In StarLogo, by contrast, students think about the actions and interactions of individual objects or creatures. StarLogo programs describe how individual creatures (not overall populations) behave. Thinking in terms of individual creatures seems far more intuitive, particularly for the mathematically uninitiated. Students can imagine themselves as individual turtles/creatures and think about what they might do. In this way, StarLogo enables learners to "dive into" the model (Ackermann, 1996) and make use of what Papert (1980) calls "syntonic" knowledge about their bodies. By observing the dynamics at the level of the individual creatures, rather than at the aggregate level of population densities, students can more easily think about and understand the population oscillations that arise. In future versions of StarLogo, we hope to add features to enable students to shift perspective from a global to an individual point-of-view.

We refer to StarLogo models as "true computational models," since StarLogo uses new computational media in a more fundamental way than most computer-based modeling tools. Whereas most tools simply implement traditional mathematical models on a computer (e.g., numerically solving traditional differential-equation representations), StarLogo provides new representations that are tailored explicitly for the computer. Of course, differential-equation models are still very useful–and superior to StarLogo-style models in some contexts. But too often, scientists and educators see traditional differential-equation models as the only approach to modeling. As a result, many students (particularly students aliented by traditional classroom mathematics) view modeling as a difficult or uninteresting activity. What is needed is a more pluralistic approach, recognizing that there are many different approaches to modeling, each with its own strengths and weaknesses. A major challenge is to develop a better understanding of when to use which approach, and why.

Conclusion: Reaching for Another Level

In the educational community, there is growing excitement about the introduction of computers into the classroom. But too often, today’s computers are used simply to teach the same old content in a slightly new package. Overall, school curricula have been hardly affected by the rush of computers into classrooms. Although some educators are using the introduction of computers as an opportunity to rethink how students should learn, very few are rethinking what students should learn.

This paper illustrates how computers can be used to introduce the concept of levels into science education. We have chosen to focus on the concept of levels since it is simultaneously:

• critically important to the understanding of many scientific phenomena and many foundational philosophical questions;

• greatly under-represented in today’s science-education curricula

• much more easily explored and understood through the use of computational media than through any previous media.

Although ideas related to levels have traditionally been taught only in advanced university courses, if at all, they touch on some of the most basic and fundmental issues in science and philosophy. Many scientific phenomena, from the pressure of a gas to the population fluctuations in an ecosystem, can best be understood through a perspective of levels. It is only through fluidly shifting between levels that learners can develop an understanding of the mechanisms underlying the patterns they see in the world – everything from the formation of traffic jams to the formation of slime-mold clusters. At the same time, the concept of levels is fundamental to developing a deep understanding of mind, of self, and of society.

Since the concept of levels is so fundamental to scientific and mathematical understanding, it is curious that it has been so absent from science and mathematics curricula. The three cases described in this paper demonstrate how the concept of levels can be effectively introduced to students (and teachers) from middle school through college. Previous studies have found that most students see science and mathematics as a collection of disconnected facts and ideas. In our research, we have found that the concept of levels provides students with a more unified framework for thinking about scientific phenomena. This unified framework helps students make connections between concepts in the curriculum that typically are taught in isolation and are often seen as unrelated.

In all three of our cases, computational tools play an important role in helping students develop an understanding of levels. By building models with StarLogo, students can explore how changes of rules on one level lead to different behaviors and patterns at another level. This shifting between levels enables students to examine the mechanisms that underlie the phenomena they see in the world. Instead of accepting phenomena as black boxes, students can look inside the boxes and even try "rewiring" them.

What is needed to bring the concept of levels into the mainstream of science and mathematics education? First, we need more fine-grained research studies that probe the conceptions that underlie the ways students understand (and misunderstand) emergent levels. Second, we need new computational tools that make it easier for students to build their own models of complex systems – and then to help them shift between levels as they experiment with those models.

But perhaps most important, we need to radically rethink the mathematics and science curriculum. We see levels as providing a new "dissection" of math and science education, offering a new way to slice up the traditional disciplines along new axes. The concept of levels is, perhaps, the most important ingredient to a more systemic approach to science learning – in which learners see mathematics and science as unified, coherent, explanatory frameworks for making sense of phenomena at multiples levels of organization. The point is not just to make connections among existing disciplines (as is advocated in most interdisciplinary approaches) or to merely shift the boundaries between existing disciplines, but to rethink the content of the disciplines that are being connected.

The approach we have outlined here can be used not only to look at math/science content but also to look at the processes of implementing educational reform policies. To bring about real change in science and mathematics education, we need think about "levels" on yet another level. It is not enough to merely introduce the concept of levels into the curriculum. We need to introduce "level thinking" into the process of educational reform. Too many educational reform efforts see reform as the accumulation of many incremental changes. To bring about real change, we need to think of educational reform itself as an emergent process.

Endnotes

^{1 Of course, the way we experience a year is not just the accumulation of our experiences of the months. But the year as a unit of time is a simple accumulation of months.}^{2 This view of corporate organization parallels recent thinking in management science, where the emphasis has shifted away from top-down control toward more network-based or participatory models in which information and decision-making flows in many different directions (Senge, 1990).}^{3 The StarLogo/T modeling language can be downloaded from /cm/ or from http://www.media.mit.edu/~starlogo}^{4 The slime model can be downloaded from http://starlogo.www.media.mit.edu/people/starlogo/projects/slime.html}^{5 The Gas-in-a-box model and the entire GasLab collection of models can be downloaded from /cm/models/}^{6 The students’ efforts to construct a measure of pressure led some of them to wonder: Does a gas in which none of the particles collide with the box have pressure? In their gas-in-a-box model, it was easy to try this "impossible" experiment (requiring a Maxwell-like demon). They placed all the particles in the center of the box and let the model "go". The resultant screen image of a supernova-like blue mass surrounded by green and then red outer layers, did not register any pressure using their pressure measure. Arguments ensued about whether their notion of pressure was thus proved inadequate. Regardless of the consistency of this notion with the classical notion of pressure, we would argue that the kind of thinking these students were doing was evidence of powerful and sophisticated physics reasoning.}^{7 Several versions of predator prey models can be downloaded from http://starlogo.www.media.mit.edu/people/starlogo/projects/rabbits.html or from /cm/models/

Acknowledgements
The preparation of this paper was supported by the National Science Foundation (Grants RED-9552950, RED-9358519, REC-9632612), The ideas expressed here do not necessarily reflect the positions of the supporting agency. Brian Silverman, Andy Begel and Rob Froemke played significant roles in the development of the StarLogo modeling environment. Walter Stroup was an invaluable contributor to the GasLab project., Ken Reisman, Ed Hazzard and Rob Froemke contributed greatly to many of the models described herein. We would like to thank Seymour Papert for his overall support and inspiration and for his constructive criticism of this research in its early stages.}

References

Ackermann, E. (1996). Perspective-taking and object construction: Two keys to learning. In Y. Kafai & M. Resnick (Eds.), Constructionism in Practice (pp. 25-35). Mahwah, NJ: Lawrence Erlbaum.

Cohen, M., & Hagan, P. (1981). Diffusion-Induced Morphogenesis in Dictyostelium. Journal of Theoretical Biology, 93, 881-908.

Dawkins, R. (1976). The Selfish Gene. Oxford: Oxford University Press.

Dennett, D. (1995). Darwin’s Dangerous Idea: Evolution and the Meanings of Life. New York: Simon and Schuster.

Forrester, J.W. (1968). Principles of Systems. Norwalk, CT: Productivity Press.

Gell-Mann, M. (1994). The Quark and the Jaguar. New York: W.H. Freeman.

Giancoli, D. (1984). General Physics. Englewood Cliffs, NJ: Prentice Hall

Gleick, J. (1987). Chaos. New York: Viking Penguin.

Jackson, S., Stratford, S., Krajcik, J., & Soloway, E. (1996). A Learner-Centered Tool for Students Building Models. Communications of the ACM, 39 (4), 48-49.

Kauffman, S. (1995). At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford: Oxford University Press.

Hofstadter, D. (1979). Godel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books.

Holland, J. (1995). Hidden Order: How Adaptation Builds Complexity. Reading, MA: Helix Books/Addison-Wesley.

Keller, E.F. (1983). A Feeling for the Organism: The Life and Work of Barbara McClintock. San Francisco, CA: W.H. Freeman.

Keller, E.F., & Segel, L. (1970). Initiation of Slime Mold Aggregation Viewed as an Instability. Journal of Theoretical Biology, 26, 399-415.

Kelly, K. (1994). Out of Control. Reading, MA: Addison Wesley.

Lotka, A.J. (1925). Elements of Physical Biology. New York: Dover Publications.

Lovelock, J. (1979). Gaia: A New Look at Life on Earth. New York: Oxford Univ. Press.

Minsky, M. (1987), The Society of Mind. Simon & Schuster Inc., New York.

Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.

Prigogine, I., & Stengers, I. (1984). Order out of Chaos: Man’s New Dialogue with Nature. New York: Bantam Books.

Resnick, M. (1994). Turtles, Termites and Traffic Jams: Explorations in Massively Parallel Microworlds. Cambridge, MA: MIT Press.

Resnick, M. (1996). Beyond the Centralized Mindset. Journal of the Learning Sciences, 5 (1), 1-22.

Resnick, M., & Wilensky, U. (1998). Diving into Complexity: Developing Probabilistic Decentralized Thinking Through Role-Playing Activities. Journal of the Learning Sciences, 7 (2), 153-171.

Roberts, N., Anderson, D., Deal, R., Garet, M., Shaffer, W. (1983). Introduction to Computer Simulations: A Systems Dynamics Modeling Approach. Reading, MA: Addison Wesley.

Roetzheim, W. (1994). Entering the Complexity Lab. Indianapolis: SAMS/Prentice Hall.

Senge, P. (1990). The Fifth Discipline. New York: Doubleday/Currency.

Tipler, P. (1992). Elementary Modern Physics. New York: Worth Publishers

Volterra, V. (1926). Fluctuations in the Abundance of a Species Considered Mathematically. Nature, 188, 558-560.

Waldrop, M. (1992). Complexity: The emerging order at the edge of order and chaos. New York: Simon & Schuster.

Wilensky, U. (1997). What is Normal Anyway? Therapy for Epistemological Anxiety. Educational Studies in Mathematics. Special Edition on Computational Environments in Mathematics Education. Noss R. (Ed.) 33 (2), 171-202.

Wilensky, U. (in press). GasLab–an Extensible Modeling Toolkit for Exploring Micro- and Macro- Views of Gases. In Roberts, N. , Feurzeig, W. & Hunter, B. (Eds.) Computer Modeling and Simulation in Science Education. Berlin: Springer Verlag

Wilensky, U. (1996). Modeling Rugby: Kick First, Generalize Later? International Journal of Computers for Mathematical Learning. 1 (1), 125-131.

Wilensky, U. (1995a). Learning Probability through Building Computational Models. Proceedings of the Nineteenth International Conference on the Psychology of Mathematics Education. Recife, Brazil, July 1995.

Wilensky, (1995b). Paradox, Programming and Learning Probability: A Case Study in a Connected Mathematics Framework. Journal of Mathematical Behavior, 14 (2).

Wilensky, U. (1993). Connected Mathematics: Building Concrete Relationships with Mathematical Knowledge. Doctoral dissertation, Cambridge, MA: Media Laboratory, MIT.

Wilensky, U. (1991). Abstract Meditations on the Concrete and Concrete Implications for Mathematics Education. In I. Harel & S. Papert (Eds.) Constructionism. Norwood NJ.: Ablex Publishing Corp.