Uri Wilensky
Center for Connected Learning and Computer-Based Modeling
Northwestern University
Annenberg Hall, 2120 Campus Drive
Evanston, IL 60208 USA
uri@northwestern.edu
To appear in @CONCORD.org, Winter 2000.
Uri Wilensky
Center for Connected Learning and Computer-Based Modeling
Northwestern University
Annenberg Hall, 2120 Campus Drive
Evanston, IL 60208 USA
Everywhere we look, we see regularities, patterns, order. Many of these patterns have a kind of haunting beauty: the growth of a snowflake crystal, the perimeter pattern of a maple leaf, the advent of a summer squall. Other patterns, such as the dynamics of the Dow Jones or of a fourth grade classroom, seem messier, inchoate, yet still exhibit a familiar and recognizable general "shape". The characteristic shape can unfold in space or in time, sometimes striking and unmistakable and sometimes more hidden, needing probing observation or ingenious experiment to uncover it.
Why is there so much pattern in the world? While grappling with this question in full would take us far afield, we can start with a simple observation: large scale patterns in the world are usually the result of the interactions of large numbers of smaller pieces that somehow combine in surprising ways to create the large-scale pattern. Such large-scale (macro-) patterns that arise out of the interactions of numerous interacting (micro-) "agents" are called "emergent phenomena" — that is, phenomena that emerge from interactions at a lower level or scale.
Visualize, a flock of birds winging in the autumn sky or the amazing synchronized fireflies that blink in unison lighting up whole trees in the far east. How do these patterns come about? All of these patterns are emergent, there is no leader bird which other birds follow, no conductor firefly leading the band -- these patterns emerge out of the behavior of individuals and the adjustment of that behavior in interaction with other individuals.
The study of emergent phenomena is the principal occupation of a developing field of science, the study of complex dynamic systems. This broad new field seeks to understand how systems of interacting components evolve over time. In the minds of many, however, complex systems theory is not a new branch of science, but rather a new framework, a new perspective that allows us to see old scientific content in new ways. This new perspective and the methods it brings to bear have been adopted across a wide array of natural and social sciences. An understanding of complex systems is becoming an essential part of every scientist’s knowledge and skills. The time has come for these ideas and methods to become a central part of every student’s learning.
Despite its adoption by practicing scientists, the complex systems perspective is largely absent from the K-16 curriculum. One reason for the slow transfer to schools is the heavy reliance of complex systems methodologies on the use of powerful computational technologies. By enabling the rendering, simulation and visualization of the evolution of complex systems over time, the computer has proved an indispensable tool for making sense of complex systems and emergent phenomena. Most of the tools used by experts to explore complexity in their domain of interest are highly domain specific — designed for use by experts to study a particular class of phenomena. Until very recently, no general purpose tools existed for students to render and explore systems of many interacting parts that can exhibit emergent behavior.
At the Center for Connected Learning and Computer-Based Modeling at Tufts University, our goal is to create computer-based tools and curricula to enable students to make sense of complexity and emergent phenomena. I will now describe a set of tools developed with the support of the National Science Foundation that enable typical secondary students to engage and make sense of complexity and emergent phenomena.
A major project accomplishment was the development of a computer modeling language (and associated materials) that would enable learners, teachers and students to create dynamic models of complex phenomena. The language we developed, called StarLogoT, is now in use by thousands of students, teachers and researchers worldwide. It is freely available on the web at /cm/. StarLogoT is one of a class of new so-called multi-agent modeling languages (AKA object-based parallel modeling languages or agent-based modeling languages) that have emerged from the complex systems community.
StarLogoT (and its mother language StarLogo) is an extension of the computer language Logo in which a user "drives" a graphical turtle on a computer screen by issuing commands such as "forward", "back", "right" and "left". In Logo, typically, the turtle is thought to carry a "pen" and, thus, draws a line when it moves. In this way, children can create geometric shapes by giving motion instructions to the turtle. In StarLogoT, however, instead of driving a single turtle, the use can drive (or, perhaps better to say, orchestrate) thousands of turtles. Instead of drawing with pens, turtles "draw" with their bodies. By that, I mean that the emergent shape of all the turtles’ positions constitutes a drawing in StarLogoT. Allow me to illustrate with a simple example in which turtles take the shape of little squares or points:
If we initiate a StarLogoT session with the command:
Create-turtles 1000
1000 little squares will appear in the graphics screen. However, because they are initialized to start in the middle of the screen, they are all piled on top of each other and appear as a single point.

Figure 1: Create-turtles 1000
If we then type the command;
Forward 40
All of the turtles move forward 40 screen units

Figure 2: Forward 40
Note that because the turtles were initialized with different "headings" (that is they faced in different directions), they made the shape of a circle. This is already a simple example of emergent behavior. The fact that there were enough turtles so that, by random chance, they were likely to fill the holes ensured that a coherent circle emerged from the motions of independent turtles.
At first glance, the reader might wonder how the turtles can do anything different and interesting if they all follow the same commands. The power of StarLogoT comes from the fact that each turtle is an independent agent. Because each turtle had an independent heading, they all moved in different directions when we typed "fd 40". Since it is possible for turtles to have as many states as the user likes, the response of turtles to the same commands can vary markedly.
In addition to this difference amongst turtles, each turtle does its own separate computation. To see how this makes a difference, we can type the command "back 40" to get all of the turtles back to the middle of the screen, then invoke the command, "forward random 40". The function "random" computes a random value between 0 and 40.Because each turtle does its own computation, each one gets a different value for "random 40" and thus will move forward a different amount.
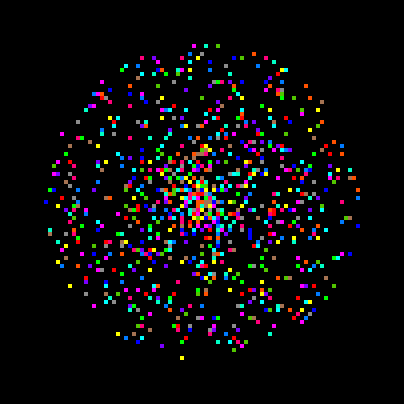
Figure 3: forward random 40
(Beginning students often want to reverse this operation and therefore try the command "back random 40". However, this has unexpected results. Try it.)
In addition to turtles, StarLogoT has a second kind of agent that we call a "patch". Patches are very much like turtles except that they are always around and do not move. The screen is initialized to a (user resizable) grid of patches. In other words, even though the graphics screen looks like empty black where there are no turtles, in reality the patches are invisibly lurking there waiting for commands.
If we type the command, "set pcolor red", all the patches will change their color to red (see figure 4).
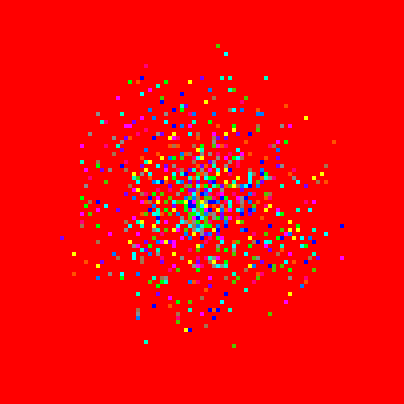
Figure 4: set pcolor red
Finally, if we type the command:
if xcor < 0 [set pcolor green]
Then all the turtles to the left of the origin turn green (see figure 5). The key point to keep in mind is that they do not do this because they are "told" to do it by a leader. They each examine their own position on the screen, determine of they are to the left of the origin and, if so, they turn themselves green.
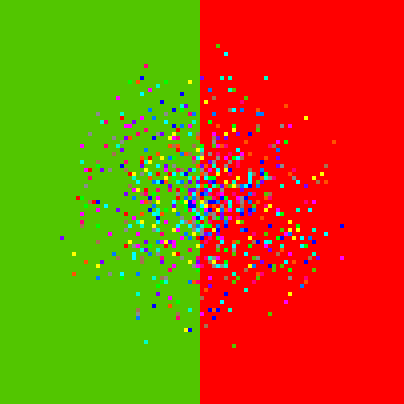
Figure 5: If xcor < 0 [set pcolor green]
With these basic tools, we can now create models and dynamic simulations of many different kinds of complex systems. There is a saying that goes: "If all you have is a hammer, the whole world looks like a nail". With the powerful hammer of the StarLogoT language, it becomes easier to see emergent phenomena everywhere . Not only the classic emergent phenomena described in the complex systems literature, but many every day and scientific phenomena can be viewed through the lens of emergent phenomena. While, at first glance, emergent phenomena seems like an exotic add-on to the curriculum, we see it as a powerful amplifier of understanding for virtually all scientific topics. By enabling us to make cogent and testable connections between the micro- and macro-, the individual and the collective, the element and the system, the new lens makes them easier to understand for novice and for expert learners alike.
I will now present two examples of the kinds of models students can build with StarLogoT. The first example is a model of a simple predator-prey ecosystem — a popular model with high school students using StarLogoT.
In a typical such model, students model a predator (say a wolf) and a prey (say a sheep). They need to give rules to individual wolves and sheep so that they can move and interact. Many sets of rules are possible. A typical set of rules might assign an energy level to each wolf and sheep and decrease their energy when they move, increase their energy when they eat (wolves eating sheep). If their energy falls below 0 they would die. At every turn, they get a random number (roll an imaginary ‘die") and if they are lucky they reproduce. Such a model is illustrated below.
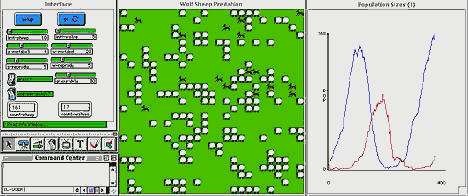
Figure 6: The StarLogoT window setup for the wolf-sheep predation model. In the upper left is the interface window that allows users to set model parameters and run simulations. In the middle is the StarLogoT graphics window which displays each individual wolf and sheep and on the right is a population plot window.
A dynamic graph of the population levels of sheep and wolves can be viewed alongside the screen. If the rule sets are chosen appropriately, a typical result is that the population graphs look like out-of-phase sine waves -- sheep populations increase till the wolves have so much to eat that they increase which reduces the population of sheep which, eventually, in turn decreases the population of wolves which results in an increase in the sheep population. (see figure 7).
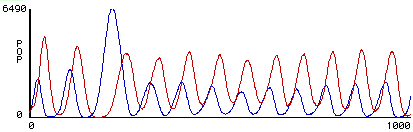
Figure 7. A typical population graph from a student rule-set. Red represents size of predator population, while blue represents size of prey population.
This is a classical result, but seen here through the lens of emergent phenomena. The students control the behavior at the micro- level of the individuals and then observe the results at the macro- level of the populations. It is through experimenting with the dynamics of this connection that a powerful understanding of the predator prey dynamics can be achieved.
A second example is a model called Gas-in-a-Box, one of a suite of StarLogoT models in a package called GasLab. Gas-in-a-Box was originally created by a physics teacher but the original model has been refined by dozens of students who have also created many variants and extensions of the original model.
The basic idea is a box containing thousands of gas molecules. Gas molecules are modeled as turtles that collide like elastic billiard balls, that is they collide with the box and with other molecules without loss of energy. The user can set the mass and speed of any molecule. The display color codes the molecules, blue for slow, green for average speed and red for fast.
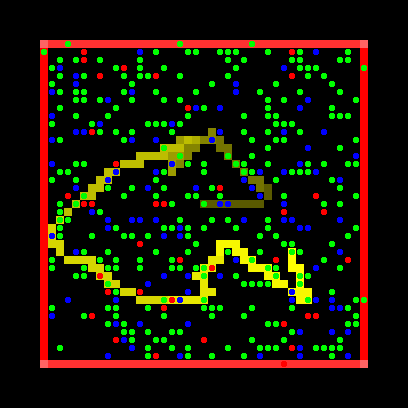
Figure 8: Gas molecules in a box. Fast particles in red, mid-speed in green and slow particles in blue. The yellow zig-zag line traces the movement of a single particle.
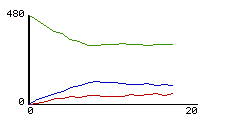 9a: plot of number of, medium, |
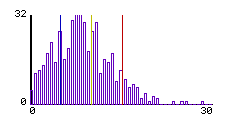
9b: histogram of particle |
Figure 9: StarLogoT displays "live" plots and histograms of the molecules in the graphics window
In a typical first use, students initialize the molecules with equal masses and equal speeds but with random positions and headings. Thus all molecules start out green. They run the model and are usually surprised to see that the molecules turn color quite quickly and that many more of them turn blue than turn green. In other words, more of the particles slow down than speed up. Although this result is a direct consequence of a known law of gases, the Maxwell-Boltzmann distribution of molecular speeds, taught in high school physics, it is not recognized by students in this form. (In our experience, not just students, but even physicists are often surprised by this result.) Again, the key insight here is that the Gas-in- a-Box model allows students to see the gas from an emergent perspective. They come to see the connection between the micro- level of billiard ball collisions and the macro- level of the general characteristics of the gas as an ensemble. These two levels of description are typically taught separately in the high school curriculum. However, it is in understanding the connection between these two levels, how one emerges from the other, that leads to a powerful understanding of statistical thermal physics. The connection has been thought to be too hard for high school students, as it usually involves advanced mathematical machinery. But, through the use of multi-agent modeling languages such as StarLogoT, these ideas can be accessible to high school learners.
StarLogoT is in use by many students, teachers and classrooms. In its years of use, we have assembled a large collection of "extensible" models (collectively entitled "Connected Models") which are available for download at ccl.northwestern.edu/cm. The sample models are drawn from a wide range of disciplines including physics, biology, mathematics, computer science, chemistry, materials science, ecology and economics. These sample models are created by students, teachers and researchers and go through a process of checkout and refinement before becoming a part of the distribution archive.
In the classroom, StarLogoT is typically used in roughly five phases:
a) In the first phase, the teacher typically leads the students in off-computer activities (known as participatory simulations or emergent activities) that provoke thinking about emergent phenomena. In these activities, students typically enact the role of individual elements of a system and then discuss amongst themselves what global patterns they detect and how those patterns could arise from their individual behaviors.
b) In the second phase, the teacher presents a "seed" model (a simple starting model) to the whole class, projected through an LCD panel so that everyone can view it. The teacher engages the class in discussion as to what is going on. Why are they observing that particular behavior? How would it be different if model parameters were changed? Is this a good model of the phenomenon it is meant to simulate?
c) In the third phase, students run the model (either singly or in small groups) on individual computers and explore the parameter space of the model.
d) In the fourth phase, each modeler (or group) proposes an extension to the model and implements that extension in the StarLogoT language. Modelers starting with GasLab, for example, might try to add to the model by building a pressure gauge, a piston, a gravity mechanism, or heating/cooling plates. The extended models are added to the project’s library of extensible models and made available for others to work with as "seed" models.
e) In the final phase, students are asked to propose a phenomenon and build a model of it from "scratch" using the StarLogoT modeling primitives.
There are other simulation software packages that enable students to engage in phases b & c. However, because the students can't inspect or modify what happens inside these simulations, they can't engage in phases d) and e) and thus go more deeply into understanding the models. This is the problem with "black-box" tools: easier to use at first, but less opportunities for learning. Yet other simulation packages, notably STELLA, are "glass-box" like StarLogoT, but they ask students to model only at the level of populations. By enabling students to model at the level of individuals, StarLogoT makes it easier for beginning students to build models because they start at the level of individual behavior. Hence they can base their models on their own experience -- experience both as individuals in the world, and of individual objects in the world..
We have worked with classrooms in all five of these phases. Generally, the depth of understanding of complex systems and emergent phenomena would be expected to increase as students start to more actively build, modify, and explore the models. The results that students can achieve with model extensions and designing their own models are often quite dramatic. Because of the great variations in available technology, learning time, and classroom organization, each phase has valuable applications.
Working in phase d), what we call the "extensible modeling" approach, allows learners to dive right into the model content. Learners typically start by exploring the model at the level of domain content. When they are puzzled by an outcome of the model, they design an extension to the basic model. This extension usually requires only a few language primitives to implement. This allows learners to follow a gently sloping path towards full StarLogoT language mastery – skill with the general purpose modeling language is acquired gradually as they seek to explain their experiments and extend the capabilities of the model.
The inclusion of a complex systems perspective in school curriculum would have many benefits for learners:
• We live in an increasingly interconnected world. Smokestacks in the Midwest cause acid rain in the Eastern US. Rainforest destruction in South America leads to Greenhouse effects and weather pattern changes in Africa. Market collapses in the Far East can wreak great consequences on economies in the West. Traditional science which studies phenomena in isolation is not equipped to analyze and understand such systemic effects. Informed citizens in such a highly interacting world need tools that can help them cope with these complexities.
• Though there is increased desire for interdisciplinary learning, students studying in a traditional curricular framework find it difficult to see the connections between different domains of knowledge. One strength of the complex systems theory perspective is that it enables us to see common patterns across traditionally separate fields: physical matter is the emergent result of molecular interactions; ecologies and biological niches are emergent results of interacting organisms; economies and markets are emergent results of the interactions of buyers and sellers.
• Many everyday phenomena and experiences arise from the interactions of many different factors. Because these have been hard to study using traditional methods, they are excluded from the curriculum. Introducing complex systems allows students’ personal experiences to be included in the curriculum — thus students see science as more personally relevant.
• An understanding of patterns as emergent phenomena, rather than as results of equations, is both a more accurate picture of nature AND easier for most people to understand. Science becomes more accessible, not less, as a result of this change in viewpoint.
By introducing a perspective of complexity and emergent phenomena, we make science more accurate, more inclusive and more accessible to the great majority of students.