


|
URI WILENSKY Center for Connected Learning Northwestern University Annenberg Hall 311 2120 Campus Drive evanston, IL 60208 uriw@media.mit.edu 847-467-3818 |
Epistemology &
Learning Group Learning & Common Sense Section The Media Laboratory Massachussets Institute of Technology 20 Ames Street Room E15-315 Cambridge, MA 02139 uriw@media.mit.edu |

|

|

|
Yet, despite the rapid infiltration of probability and statistics into our science and media, there is substantial documentation of the wide spread lack of understanding of the meaning of the statistics we encounter (Gould, 1991; Konold, 1991; Phillips, 1988; Piaget, 1975; Tversky & Kahneman, 1971). Even highly educated professionals who use probability and statistics in their daily work have great difficulty interpreting the statistics they produce (Kahneman & Tversky, 1982).
Besides a lack of competence and understanding, students express a great deal of dislike towards courses in probability and statistics„an antipathy well captured by the oft-quoted line, attributed to both Mark Twain and Benjamin Disraeli: "There are three kinds of lies: lies, damn lies and statistics."
Most students first encounter the subject of probability in the form of school exercises in calculating ratios of frequencies and binomial coefficients. As a result, the subject matter of probability and statistics is seen as an assemblage of formulae to be committed to memory. When students fail to master the techniques taught to them, better methods are sought to improve their ability to calculate and apply the formulae. But very little is done in school to explore basic ideas of probability or respond to questions such as: "what is a normal distribution and what makes it useful?" or "how can something be both random and structured?" Partially because the meanings of core probabilistic notions are still being debated by philosophers of mathematics and science (e.g., Chaitin, 1987; Kolmogorov, 1950; Savage, 1954; Suppes, 1984; von Mises, 1957), it is assumed that these meanings are too hard for students to access. "Safe probability" is best practiced through formal exercises without too much attention to the meanings of underlying concepts.
There is a substantial literature concerning the topic of decision-making under uncertainty (e.g., Cohen, 1979; Edwards & von Winterfeldt, 1986; Evans, 1993; Kahneman & Tversky, 1973; 1982; Nisbett, 1980; Nisbett, Krantz, Jepson & Kunda, 1983; Tversky & Kahneman, 1974; 1980; 1984). Much of this literature documents the systematic errors and biases people display when attempting to make judgments under uncertainty. A common conclusion drawn by educators and researchers from this research is that "people just aren't built for doing probability," our intuitions are faulty and are not to be trusted. So, again, the safe practice for educators wishing their students to master the material is to instill in them a mistrust of their intuitive responses and a healthy respect for the formulae[1].
The cost of this highly formal instruction in probability and statistics is high. While the best and brightest do manage to learn to use the right statistical tests in the appropriate contexts, even they do not really understand what they are doing. They experience a kind of "epistemological anxiety" (Wilensky, 1993; in preparation, 1994) - anxiety about the nature of the knowledge they are producing and what justifies it. This anxiety leads to skepticism about the validity of statistical knowledge. Add to this mix the unscrupulous use of statistical arguments to mislead voters and consumers and we begin to understand why the subject stimulates so much distaste. The cost of this educational approach is to deprive learners from accessing core probabilistic and statistical notions which are powerful means of making sense of the world.
In this paper, I present a case study of a learner engaged in a classical probability paradox. The learner was one of seventeen interviewees studied in depth as part of the Connected Probability project. I start by briefly describing the Connected Probability project and its theoretical framework„the Connected Mathematics research program. Part of the learning environment provided in the Connected Probability project is a computer modeling language suitable for probability investigations - a version of the language Starlogo (Resnick, 1992; Wilensky, 1993). I, then, present the probability paradox with which the subject is engaged and an account of her investigation. The paradox was selected because of its potential for engaging learners in a deeper investigation into the meaning of the concept of "random" - a fundamental concept of probability theory. I conclude by arguing three points illustrated in the case study: 1) that providing support for seriously engaging such paradoxes is an important avenue to relieving epistemological anxiety about the nature of probabilistic concepts; 2) that programming can be an effective tool for resolving mathematical paradoxes (by making their hidden assumptions[2] explicit and concrete) and 3) that through programming their own computational models (and thus making their own mathematics), learners gain a much deeper understanding of probabilistic concepts than through the use of simulations or pre-built computational models.
The Connected Mathematics approach is rooted in the constructionist (Papert, 1991; 1993) learning paradigm. As such, it holds that the character of mathematical knowledge, is inextricably interwoven with its genesis Ü both its historical genesis and its development in the mathematical learner. A conception of mathematics as disconnected from its development leads to the misguided pedagogy of the traditional mathematics curriculum - a "litany" of defintion-theorem-proof and its attendant concepts stipulated by formal definition[4]. In contrast to approaches that attempt to explain failures of mathematical understanding in technical or information processing terms, Connected Mathematics seeks to explain these obstacles in epistemological terms. Obstacles to understanding are failures of meaning making and since meaning is made through building connections, Connected Mathematics sees these as fundamentally failures of connection.
Paradox can be an important tool of a Connected Mathematics learning environment. The recognition of paradox, is the recognition that (at least) two conceptual structures have not been integrated. This explicit recognition is the first step in making the connections between the two structures that will resolve the paradox and, most often, thereby, generate new mathematics.
The vision of mathematics as being made and not simply received leads naturally to a role for technology. Technology is not there simply to animate received truth, it is an expressive medium Ü a medium for the making of new mathematics. It follows that we can make better use of computational technologies than simply running black-box simulations Ü we can make mathematics by constructing computational embodiments of mathematical models. The true power of the computer will be seen not in assisting the teaching of the old topics but in transforming ideas about what can be learned.
Technology here is to be construed in a broad sense Ü the notations in which we express mathematics and the mathematical concepts themselves are artifacts of the technology of the period of their creation. The emergence of new powerful computational technologies, therefore implies a radical change in both the concepts and semiotic activities of a newly contextualized mathematics.
In contrast to the NCTM Standards, which portrays an "image" of mathematics (see Brandes, 1994) as essentially a problem solving activity, the vision of Connected Mathematics is more generative„the central activity being making new mathematics. In so doing, it fosters a culture of design and exploration„designing new representations of mathematics and encouraging critique of those designs.
Connected Mathematics acknowledges and attends to the affective side of learning mathematics and looks critically at the role of shame in the mathematical community. Listening to learners and fostering an environment in which it becomes safe for mathematical learners to express their partial understandings[5] results in a dismantling of the culture of shame which paralyzes learners - preventing them from proposing the tentative conjectures and representations necessary to make mathematical progress. In doing so, it parts company with the literature on misconceptions which highlights the gulf between expert and novice. Instead, Connected Mathematics stresses the continuity between expert and novice understanding[6], noticing that even expert mathematicians have had to laboriously carve out small areas of well connected clarity from the generally messy terrain (see also Smith, diSessa, & Roschelle, 1994).
These topics were valuable for gaining insight into people's ideas about probability, and encouraging them to think through probabilistic issues. In one sense probability is ubiquitous in our everyday lives. Yet, since probability is fundamentally about large numbers of instances, these singular everyday experiences may not be useful for building our probabilistic intuition[8]. Rarely, in our everyday lives, do we have direct and controlled access to large numbers of experimental trials, measurements of large populations, or repeated assessments of likelihood with feedback. We do regularly assess the probability of specific events occurring. However, when the event either occurs or not, we don't know how to feed this result back into our original assessment. After all, if we assess the probability of some event occurring as, say, 30%, and the event occurs, we have not gotten much information about the adequacy of our original judgment. Only by repeated trials can we get the feedback we need to evaluate our judgments. Without the necessary feedback, it is difficult to develop our probabilistic intuitions and make probabilistic concepts concrete.
A powerful way to bridge this gap between singular experiences and probabilistic reasoning is through the use of exploratory computational environments. The processing power of the computer can give learners immediate access to large amounts of data usually distributed widely over space or time. This can provide the necessary feedback needed to develop concrete understandings of probabilistic concepts. In creating an environment for learning probability, it is therefore natural to consider computational tools.
One of the investigatory tools made available to the learners in this study was a programming language, Starlogo (Resnick, 1992; Wilensky, 1993) specially adapted for modeling probabilistic phenomena. Starlogo is a massively parallel version of the computer language Logo. It allows the user to control thousands of "turtles" on a computer screen. Each of the turtles (or agents) has its own local state and can be given its own local procedures and rules of interaction[9]. Thus, the user can model the emergent effects of the behavior of many distributed agents each following its own local rules. In particular, the key probabilistic notion of distribution can be seen to arise from the actions of many independent agents (see Wilensky, in preparation, 1994). Starlogo facilitates the design of probability experiments which allow learners to test their conjectures. They can use the feedback to modify them and clarify their underlying structures via successive refinement (Leron, 1983). The use of Starlogo to design probability experiments is in keeping with the constructionist (Papert, 1991) model of learning„that a particularly felicitous way to build strong mental models is to produce physical or computational constructs which can be manipulated and debugged. As we shall see in the case that follows, being able to articulate a model of a probabilistic concept (through programming) can lead to rich insights into the nature of probabilistic concepts such as randomness and distribution. In contrast to consumers of ready made models, learners who construct computational models are afforded the opportunity to refine their models through debugging. Through debugging their programs they can debug their probabilistic concepts and make them concrete (Wilensky, 1991).
In the case reported on below, the paradoxical element was introduced by the interviewer. Once that intervention occurred, no further support was needed for the interviewee to recognize it as a paradox[11]. The resolution of the paradox, however, was greatly facilitated by use of the programming language.
Some researchers and educators have recently argued that students cannot make practical use of general purpose programming languages in their subject domain learning (e.g., Soloway, 1993; Steinberger, 1994)[12]. It is my hope that the case study below will help dispel this claim and show the interesting and productive interactions that can occur between programming and learning mathematics. Indeed, it is through programming that the interviewee first "thickens" (Geertz, 1973) her understanding of "random" - by seeing the need for a process, be it computational or physical, to generate randomness. Thus, a computational idea leads to a mathematical idea, resulting in the recognition of the intimate tie between a random process and a probability distribution[13]. This thickening of the notion of random and embedding it in a web of related concepts and activities leads to a Connected Mathematics understanding of randomness[14].
Each of the answers listed above is in fact the correct answer for a particular probability experiment. Depending on the physical experiment conducted, or, in the corresponding mathematical language, the initial distribution that is assigned to the chord lengths, different answers will be obtained. By exploring the paradox, learners came to see there was no unique way to specify a "random chord" (or in one interviewee's language "there's no such thing as a random chord"). Different ways of choosing chords are appropriate for different occasions. Different physical experiments lead to different probabilities and correspond to different ways of choosing chords. Depending on which method is used to select chords, different distributions of chord lengths will ensue. This leads to seeing the deep and powerful connections between randomness, distributions and physical experiments. It lays the intuitive substrate needed to create probabilistic models and to make sense of more advanced probability concepts such as probability measures.
Many interviewees answered this question fairly quickly using the following argument. Chords range in size from 0 to 2r. Since we're picking chords at random, they're just as likely to be shorter than "r" as they are to be longer than "r". Hence the probability is equal to 1/2.
Ellie engaged herself with this question but approached it differently. She began thinking about the problem by drawing a circle and a chord on it which she knew had length equal to the circle's radius, as shown below. (See figure 1).
After contemplating this drawing for a while, she then drew the following figure: (See Figure 2).
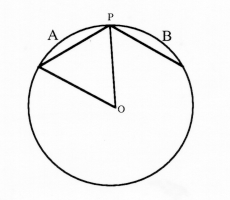
Ellie: It has to be equilateral because all the sides are equal to a radius. So that means six of them fit around a circle. That's right, 6 * 60 = 360 degrees. So, that means if you pick a point on a circle and label it P, then to get a chord that's smaller than a radius you have to pick the second point on either this section of the circle [labeled A in the figure above] or this one [labeled B in the figure above]. So since each of those are a sixth of the circle, you get a one third chance of getting a chord smaller than a radius and a two thirds chance of a chord larger than a radius.[15]
Ellie was quite satisfied with this answer and I believe would not have pursued the question any more if not for my prodding.
E: Really? I don't see how that could be.
U: Can I show you?
E: Sure. But I bet it's got a mistake in it and you're trying to trick me.
U: OK. Let me show you and you tell me.
I, then, drew the figure below: (See Figure 3)
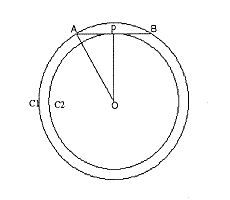
This explanation had a disquieting effect on Ellie. She went over it many times but was not able to find a "bug" in the argument. After repeatedly struggling to resolve the conflict, she let out her frustration:
E: I don't get it. One of these arguments must be wrong! The probability of choosing a random chord bigger than a radius is either 2/3 or 3/4. It can't be both. I'm still pretty sure that it's really 2/3 but I can't find a hole in the other argument.
U: Can both of the arguments be right?
E: No. Of course not.
U: Why not?
E: It's obvious! Call the probability of choosing a chord larger than a radius p. Then argument #1 says p = 2/3 and argument #2 says p = 3/4. If both argument #1 and #2 are correct then 2/3 = 3/4 which is absurd.[16]
Here Ellie is quite sure that there is a definite and unique meaning to the concept "probability of choosing a random chord larger than a radius" even though she admits that she is not completely certain what that meaning is.
E: Good idea. I can program up a simulation of this experiment and compute which value for the probability is correct! I should have thought of that earlier.
Ellie then spent some time writing a Starlogo program. As she worked to code this up, she soon began to feel uneasy with her formulation. A few times she protested: "But I have to generate the chords somehow. Which of the two methods shall I use to generate them?" Nevertheless, she continued writing her program, using an approach based on argument #1. Basically, she made each turtle turn randomly and move forward a distance equal to the circle's radius to pick a point on the circle. Then, she made the turtle return to the center, turn randomly again, and move forward to pick a second point on the circle, thus defining a chord. At various points, she was unsure how to model the situation. She experimented with using the same radius for each turtle as well as giving each turtle its own radius. She experimented with calculating the statistics over all trials of each turtle as opposed to calculating it over all the trials of all the turtles. Finally, she decided both were interesting and printed out the "probability" over all trials as well as the minimum and maximum probability of any turtle.
Below are the main procedures of Ellie's program. Comments (preceded by semi-colons) have been added by the author for clarity of the exposition.
TURTLE PROCEDURES[17]
;;; this turtle procedure sets up the turtles[18] to setup
setxy 0 0 ;;; place myself at the origin
make "radius 10 ;;;; make my radius 10 units
make "p1x 0 ;;;; initialize temporary variables
make "p1y 0
make "p2x 0
make "p2y 0
make "chord-length 0
make "trials 0
make "big 0
make "prob 0
end
;;; This is a turtle procedure which generates a random chord.
to gen-random-chord
fd :radius ;;;; go to the circumference of
the circle
make "p1x xpos ;;;; remember where I am
make "p1y ypos bk :radius ;;;; go back to the center of the
circle
(the origin)
rt random 360 ;;;; turn randomly
fd :radius ;;;; go to a new point on the
circumference of the circle
make "chord-length distance :p1x :p1y ;;;; the chord length is the
distance from where I was
before to where I am now
bk :radius ;;;; go back to the center of
the circle (the origin)
end
;;;; this turtle-procedure gets executed by each turtle at each tick of
the clock
to turtle-demon
gen-random-chord ;;;; choose a new chord by the
procedure above
make "trials :trials + 1 ;;;; increment the number of
chords chosen
if bigger? [make "big :big + 1] ;;;; if the new chord is bigger than
the radius,increment the number
of chords chosen so far which are
bigger than the radius
make "prob :big / :trials ;;;; the probability (so far) of
choosing a chord bigger than the
radius is the proportion of
chords chosen so far which are
bigger than the radius
end
;;;; is the turtle's chord bigger than a radius? to bigger?
:chord-length > :radius ;;;; return "true" if chord
chosen is bigger than the radius
end
OBSERVER PROCEDURES
;;;; observer-demon summarizes the results of all the turtles
;;;; it gets executed at every clock tick.
to observer-demon
make "total-trials turtle-sum [:trials] ;;;; get the total number of
chords chosen by all
the turtles
make "total-big turtle-sum [:big] ;;;; get the total number of
chords chosen by all the
turtles bigger than a radius
make "total-prob :total-big / :total-trials ;;;; the final probability of
choosing a chord bigger than
a radius is the ratio
of the above two totals
every 10 [type :total-big type :total-trials
print :total-prob type turtle-min [prob] ;;;; print some
statistics
including the
probabilities of
the turtles with
the smallest and
largest probabilities
print turtle-max [prob]]
end
Ellie ran her program and it indeed confirmed her original analysis. On
2/3 of the total trials the chord was larger than a radius. For a while
she worried about the fact that her extreme turtles had probabilities
quite far away from 2/3, but eventually convinced herself that this was OK
and that it was the average turtle "that mattered".But Ellie was still bothered by the way the chords were generated.
E: OK, so we got 2/3 as we should have. But what's bothering me is that if I generate the chords using the idea you had then I'll probably get 3/4[19]. Which is the real way to generate random chords? (emphasis added)
The need to explicitly program the generation of the chords precipitated an epistemological shift. The focus was no longer on determining the probability. It now moved to finding the "true" way to generate random chords. This takes Ellie immediately into an investigation of what "random" means. At this stage she is still convinced, as she was before about the probability, that there can be only one set of random chords. She assumes that the problem is to discover this unique set.
U: That's an interesting question.
E: Oh, I see. We have two methods for generating random chords-what we have to do is figure out which produces really random chords and which produces non-random chords. Only one of these would produce really random chords and that's the one that would work in the real world.
U: The real world? Do you mean you could perform a physical experiment?
E: Yes. I suppose I could. ...Say we have a circle drawn on the floor and I throw a stick on it and it lands on the circle. Then the stick makes a chord on the circle. We can throw sticks and see how many times we get a chord larger than a radius.
U: And what do you expect the answer to be in the physical experiment?
E: Egads. (very excitedly) We have the same problem in the real world!!! We could instead do the experiment by letting a pin drop on the circle and wherever the pin dropped we could draw a chord with the pin as midpoint. Depending on which experiment we try we will get either answer #1[20] or #2. Whoa, this is crazy. So which is a random chord? Both correspond to reality?..... This was a breakthrough moment for Ellie, but she was not done yet. Though her insight above suggests that both answers are physically realizable, Ellie was still worried on the "mathematics side" that one of the methods for generating chords might be "missing some chords" or "counting chords twice". Ellie needed to connect her insight about the physical experiment to her knowledge about randomness and distribution. She spent quite a bit of time looking over the two methods for generating chords to see if they were counting "all the chords once and only once". She determined that in her method, once she fixed a point P, there was a one-to-one correspondence between the points on the circle and the chords having P as an end-point. She concluded therefore that there "are as many chords passing through P as there are points in the circle". However, there will be more chords of a large size than chords of a small size. As could be seen from her original argument, there will be twice as many chords of length between r and 2r as there are of chords of length between 0 and r. Now, for the first time, Ellie advanced the argument that many interviewees had given first.
E: I never thought of the obvious. I've been sort of assuming all along that every chord of a given size is equally likely. But if that were true then I could have solved this problem simply. Each chord would have an equal chance of being of length between 0 and the diameter. So half the chords would be bigger than a radius and half smaller.
Ellie went on to see that, in argument #2, large chords are more probable than small chords. She reasoned that for every chord of a given size (or more accurately a small size interval) there was a thin annulus of points that would generate chords of that size by method #2. Annuli closer to the center of the circle would correspond to large chords and annuli near the circumference would correspond to small chords. She went on to demonstrate that annuli close to the center would have larger areas than annuli close to the circumference. Thus large chords become increasingly more probable[21].
Another interesting feature: The program that Ellie wrote placed all the turtles at the origin and since Ellie, as a professional programmer, wrote state transparent code[22] they stayed at the origin. Initially, she had placed the turtles at the origin of the screen's coordinate system because she recognized a potential bug in her program. If she created the turtles in random positions as is typical in Starlogo the turtles might "wrap"[23] around the screen when drawing their circles and thus incorrectly calculate their chord lengths. But, because the turtles remained centered at the origin, the program was not very visually appealing. While we were engaged in the interview, a student came by and watched. He asked us why nothing was happening on the screen. Ellie explained what she was investigating and then had an idea of how to make the program more interesting. She decided to spread the turtles out a bit so each could be seen tracing its circle, turning yellow if its chord was longer than a radius and green if it was shorter. To spread the turtles out without getting too close to the screen edge, Ellie told each turtle to execute the command fd random (60 - radius) telling each turtle to move a random amount out from the origin. In doing this, the result wasn't quite what Ellie had hoped for. Near the origin there was a splotch of color [mostly yellow] as all the turtles were squeezed together very tightly, while near the edges the turtles were spaced out more sparsely (as in the following figure). (See figure 4)
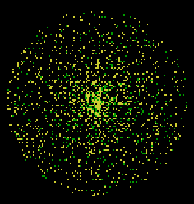
So Ellie's function which successfully spread turtles out evenly (and what she then called randomly) along a line did not spread them out evenly on the planar screen. This experience was an important component of her subsequent "aha" moment-exposing her as it did to a crack in her solid and fixed notion of "random".
By the time Ellie had gotten to the circle chords question, she had already spent five and a half hours during three separate days over a three-week period in a Connected Mathematics interview. During this time, she had encountered and constructed many paradoxes and, along the way, gained confidence in her ability to resolve them to her satisfaction. She, therefore, did not need much support on this occasion in accepting the paradox as an opportunity for learning. She took both arguments (her own and the interviewer's) seriously. Even though she suspected that the interviewer's argument was a clever trick, she felt a need to find a flaw in that argument. This need to find a flaw in one side of the paradox (as opposed to just embracing the argument that seems good to her) is a powerful avenue for learning. Less sophisticated learners are content to find an argument they can believe and do not feel a need to refute any counterarguments. Seizing on the plausible argument without refuting the counterargument was a common phenomenon in the interviews and was particularly salient in discussions of the Monty Hall family of problems (Gilman, 1992; Wilensky, 1993).
One such package, ConStats (Cohen, Smith, Chechile & Cock, in press), was designed with the objective of helping students gain "a deep conceptual understanding of introductory probability and statistics" through an "active experimental style of learning" (Cohen, Chechile, Smith, Tsai & Burns, 1994). As such, it is based in constructivist principles. However, the experiments students can conduct with ConStats consist of manipulating the parameters of a preconceived model. Students cannot program in ConStats or build models to pursue questions that arise.
The software is impressive, with well implemented graphics, an easy-to-learn user interface, extensive contextual help facilities, and a large selection of features. A principal emphasis of the software package is on distributions. The package contains many different distributions, both continuous and discrete, each with its own name and associated text describing its characteristics. In addition, for each kind of distribution, users have a host of parameters which they can manipulate and view the resultant change in the graph of the "random variable".
ConStats has both the strengths and weaknesses of the broader class of what can be called "black-box" simulations (i.e., simulations in which the user does not have explicit access to the modeling algorithm). These strengths include the ability of users to engage quickly with high level models, the availability of specialized domain specific tools, engaging user interfaces and broad coverage of the subject domain. The chief weakness is the lack of "read/write" access to the model. As a result, learners cannot explore what processes govern the way the parameters change the model. More importantly, they cannot explore the consequences of changing the structure of these processes themselves. As a result, they do not develop a solid understanding of these underlying processes.
The ConStats software was used extensively by students in a number of university-level courses. After each course was completed, the students were given a post-test designed to measure their comprehension of concepts "covered" by the software. The researchers conducting the evaluation (Cohen et al., 1994) report that conceptual comprehension was significantly greater for those students using the software than for the control group. One of the questions on the post-test was: "What is it about a variable that makes it a random variable?" The first author of the evaluation study reported (Cohen, 1993) that in all the exams he has seen, not a single student had "given the correct answer", nor had a single one mentioned the concept of distribution in his/her answer[31]. Most students just left it blank. The most frequent non-blank answer was: "a variable that has equal probability of taking on any of its possible values". Despite the fact that they had spent hours manipulating distributions and had plotted and histogrammed their "random variables," they missed the connection between these activities and the concept of random variable. The connection between distribution and randomness was perhaps too obvious to the software designers. They did not recognize the necessity of the learners constructing that connection for themselves if they are to explore it further through the software.
The ConStats software encourages exploration through changing parameters which may explain its success in improving conceptual understanding in courseware subject matter. But ConStats users' understanding of randomness is seemingly impoverished. They have not made connections between the distributions they manipulated and observed and the concept of random variable. It is unlikely that they have developed a widely-connected and intuitive sense of the concept of randomness. In contrast, most of the interviewees in the Connected Probability project developed a deeper understanding of randomness. By explicitly confronting the question of the meaning of randomness and by explicitly representing it in a program, the interviewees developed strong intuitions that were not developed by the users of the courseware.
Leaving aside the differences in conceptual understanding promoted by the two approaches, there is also an important issue of educational goals. Particularly in the area of statistics, the educational goal should emphasize interpreting and designing statistics from science and life rather than mastery of curricular materials. In order to make sense of scientific studies, it is not sufficient to be able to verify the stated model; one needs to see why those models are superior to alternative models. In order to understand a newspaper statistic, one must be able to reason about the underlying model used to create that statistic[32] and evaluate its plausibility. For these purposes, building probabilistic and statistical models is essential.
Computer-based exploratory environments for learning probability can facilitate greater conceptual understanding. The computer's capacity to repeat and vary large numbers of trials, ability to show the results of these trials in compressed time (and often in visual form), makes it possible to encapsulate events that are usually distributed over time and space. This can provide learners with the kinds of concrete experiences they need to build solid probabilistic intuitions.
A central issue, then, is between learners using pre-built models and learners making their own models. The ability to run pre-built models interactively is an improvement over static textbook based approaches. By manipulating parameters of the model, users can make useful distinctions and test out some conjectures. The results of the Connected Probability project suggest that for learners to make use of these pre-built models, they must first build their own models and design their own investigations.
It is possible to combine the two approaches (e.g. Eisenberg, 1991; Wilensky, forthcoming-b, 1994) by providing pre-built models that are embedded in programming environments, creating so-called "extensible applications" (Eisenberg, 1991). This combined approach has the advantages of both pre-built and buildable models. The challenge of such an approach is to design the right middle level of primitives so that they are neither (a) too low-level, so that the application becomes identical to its programming language, nor (b) too high-level, so that the application turns into an exercise of running pre-conceived experiments. The metric by which the optimal level can be judged is in the usefulness to learners. This requires an extensive research program. The findings from this research must inform the development enterprise.

|

|

|
In the Connected Probability project, learners such as Ellie succeeded in making deep probabilistic arguments that probed at the foundations of the discipline. Having understood the foundational concepts in this deep way, they developed a strong intuitive understanding of such concepts as randomness, distribution and expectation. Solid intuitions about probability and statistics were clearly developed by learners in this study. This shows that we are not, by our natures, as some have argued, unable to reason intuitively about probability.
The Connected Probability project is an instantiation of the Connected Mathematics approach. The key elements of the Connected Mathematics approach that enabled these changes are:
Like Ellie, they saw the connections between representations of randomness in different domains including physical experiments, probability distributions and computational processes.
Ellie focused on what it means for something (a process) to be random? Is there only one way of choosing chords randomly or can there be multiple ways?
The paradox reinforced the focus on epistemological issues - it placed her epistemology of mathematics in doubt. Ellie wondered: What kind of discipline is mathematics if a "unique" probability can be equal to both 2/3 and 3/4?
Even though the random chord problem started out as a classic formal problem, Ellie engaged herself with it to see it as her own.
Ellie would not have engaged herself with the paradox had she not been encouraged to believe in the pursuit enough to overcome the epistemological anxiety that usually prevents learners from getting so engaged. Crucial to this self-confidence is a "cognitive-emotive" therapy for the sense of shame produced by a mathematical culture that prevents learners from expressing the epistemological anxiety and tentative understandings that are at its root.
Ellie is encouraged to create alternate representations of the problem and work out definitions of randomness that make sense to her. This enables her to see mathematics as a personal odyssey of meaning making, not an externally given corpus to be assimilated but not affected by her.
Ellie was able to design her own experiment to explore the different sides of the paradox. This ability to express her partial understandings of "random chord" in a computational model was key to the refinement of her mental model and provided a powerful semiotic context for her articulation of her mathematical thought.
For many learners in the Connected Probability project, this experience of doing Connected Mathematics was so different from their experience in regular mathematics classrooms, that they did not recognize their activity as being mathematics. Learners who had "always hated mathematics" and had been told that they were not "good at mathematics" were excitedly engaged in doing mathematics that could be easily recognized by mathematicians as "good mathematics". Having created a strong intuitive foundation for the conceptual domain, learners could also go on to engage the formal approaches and techniques with an appreciation for how they connect to core idea of probability and statistics. Even more importantly, they now understood that mathematics is a living growing entity which they could literally make their own.

|

|

|
Abelson, Hal & Goldenberg, Paul. (1977). Teacher's Guide for Computational Model of Animal Behavior. LOGO Memo NO. 46. Cambridge, MA.
Ball, Deborah. (1990). With an eye on the Mathematical Horizon: Dilemmas of Teaching. Paper presented at the annual meeting of the American Educational Research Association, Boston, MA.
Belenky, Mary, Clinchy, B., Goldberger, N., & Tarule, J. (1986). Women's Ways of Knowing. New York: Basic Books.
Bertrand, Joseph. (1889). Calcul des Probabilits. Paris: Gauthier-Villars.
Borel, Emil. (1909). Elments de la Thorie des Probabilitis. Paris: Hermann et Fils.
Brandes, Aaron. (1994). Elementary School Children's Images of Science. in Yasmin Kafai and Mitchel Resnick (Eds.), Constructionism in Practice: Rethinking Learning and Its Contexts. Presented at the National Educational Computing Conference, Boston, MA, June 1994. The MIT Media Laboratory, Cambridge, MA.
Chaitin, Gregory (1987). Information, Randomness and Incompleteness: Papers on Algorithmic Information Theory. Singapore; Teaneck, NJ: World Scientific.
Cohen, B. (1990). Scientific Revolutions, Revolutions in Science, and a Probabilistic Revolution 1800-1930. In Kruger, Lorenz, Daston, Lorraine, & Heidelberger, Michael. (Eds.) The Probabilistic Revolution Vol. 1. Cambridge, MA: MIT Press.
Cohen, J. (1979). On the Psychology of Prediction Whose is the Fallacy? Cognition, 7, pp. 385-407.
Cohen, Steven. (1993). Personal Communication. Tufts University, Medford, MA.
Cohen, Steven, Smith, George, Chechile, Richard & Cock, R. (in press). Designing Curricular Software for Conceptualizing Statistics. Proceedings of the 1st Conference of the International Association for Statistics Education.
Cohen, Steven, Chechile, Smith, Richard, George, Tsai, F. & Burns, G. (1994). A method for evaluating the effectiveness of educational software. Behavior Research Methods, Instruments & Computers, 26 (2), pp. 236-241.
Cohen, Steven. (1995). Personal Communication. Tufts University, Medford, MA.
Collins, Allan & Brown, John Seeley. (1988). The Computer as a Tool for Learning Through Reflection. In Heinz Mandl & Alan Lesgold (Eds). Learning Issues for Intelligent Tutoring Systems (pp. 1-18). New York: Springer Verlag.
Confrey, Jere. (1993a). A Constructivist Research Programme Towards the Reform of Mathematics Education. An introduction to a symposium for the Annual Meeting of the American Educational Research Association, April 12-17, 1993 in Atlanta, Georgia.
Confrey, Jere. (1993b). Learning to See Children's Mathematics: Crucial Challenges in Constructivist Reform, In Kenneth Tobin (Ed.) The Practice of Constructivism in Science Education. Washington, D.C.: American Association for the Advancement of Science. pp. 299-321.
Cuoco, Alfred. & Goldenberg, Paul. (1992). Reconnecting Geometry: A Role for Technology. Proceedings of Computers in the Geometry Classroom conference. St. Olaf College, Northfield, MN, June 24-27, 1992.
Edwards, Laurie. (in press). Microworlds as Representations. in Noss, Richard., Hoyles, Celia, diSessa Andi and Edwards, Laurie. (Eds.) Proceedings of the NATO Advanced Technology Workshop on Computer Based Exploratory Learning Environments. Asilomar, Ca.
Edwards, W. & von Winterfeldt, Detlof. (1986). On Cognitive Illusions and their Implications. Southern California Law Review, 59(2), 401-451.
Evans, J. (1993). Bias and Rationality. In Mantkelow & Over (Eds.) Rationality (in press) London: Routledge.
Eisenberg, Michael. (1991). Programmable Applications: Interpreter Meets Interface. MIT AI Memo 1325. Cambridge, Ma., AI Lab, MIT.
Feurzeig, Wally. (1989). A Visual Programming Environment for Mathematics Education. Paper presented at the fourth international conference for Logo and Mathematics Education. Jerusalem, Israel.
Geertz, Clifford. (1973). The Interpretation of Cultures. New York: Basic Books.
Gigerenzer, G. (1990). The Probabilistic Revolution in Psychology „ an Overview. In Kruger, Lorenz, Daston, Lorraine, & Heidelberger, Michael. (Eds.) The Probabilistic Revolution. Vol. 1. Cambridge, Ma: MIT Press.
Gilligan, Carol. (1977). In a Different Voice: Psychological Theory and Women's Development. Cambridge, MA: Harvard University Press.
Gillman, Larry. (1992). The Car and the Goats. American Mathematical Monthly, Volume 99, number 1, January, 1992.
Gould, Stephen Jay. (1991). The Streak of Streaks. In Gould, Stephen Jay Bully for Brontosaurus. Cambridge, MA., W.W. Norton. (Chapter 31).
Hacking, Ian. (1990). Was there a Probabilistic Revolution 1800-1930? In Kruger, Lorenz, Daston, Lorraine, & Heidelberger, Michael. (Eds.) The Probabilistic Revolution. Vol. 1. Cambridge, Ma: MIT Press.
Harel, Idit. (1992). Children Designers. Norwood, NJ: Ablex. Harel, Idit & Papert, Seymour. (1990). Software Design as a Learning Environment. Interactive Learning Environments Journal. Vol.1 (1). Norwood, NJ: Ablex.
Kafai, Yasmin & Harel, Idit. (1991). Learning through Design and Teaching: Exploring Social and Collaborative Aspects of Constructionism. In Idit Harel & Seymour Papert (Eds.) Constructionism. Norwood, N.J. Ablex Publishing Corp. Chapter 5.
Kahneman, Daniel, & Tversky, Amos. (1982). On the study of Statistical Intuitions. In Daniel Kahneman, Amos Tversky, & Paul Slovic (Eds.) Judgment under Uncertainty: Heuristics and Biases. Cambridge, England: Cambridge University Press.
Kahneman, Daniel, & Tversky, Amos. (1973). On the Psychology of Prediction. Psychological Review, 80 (4), pp. 237-251.
Kaput, Jim. (1989). Notations and Representations. In Von Glaserfeld, Ernst. (Ed.) Radical Constructivism in Mathematics Education. Netherlands: Kluwer Academic Press.
Keller, Evelyn Fox. (1983). A Feeling for the Organism: The Life and Work of Barbara McClintock. San Francisco, CA: W.H. Freeman.
Keynes, John Milton. (1921). A Treatise on Probability. London: MacMillan.
Kolmogorov, Andrei (1950). Foundations of the Theory of Probability. New York: Chelsea Pub. Co.
Konold, Cliff. (1991). Understanding Students' Beliefs about Probability. In Von Glaserfeld, Ernst. (Ed.) Radical Constructivism in Mathematics Education. Netherlands: Kluwer Academic Press.
Lakatos, Imre. (1976). Proofs and Refutations. Cambridge: Cambridge University Press.
Lampert, Magdalene. (1990.). When the Problem is not the Question and the Solution is not the Answer: Mathematical Knowing and Teaching. In American Education Research Journal, spring, Vol. 27, no. 1, pp. 29- 63.
Leron, Uri & Zazkis, Rina. (1992). Of Geometry, Turtles, and Groups. In Hoyles, Celia. & Noss, Richard. (Eds.) Learning Mathematics and LOGO. London: MIT Press.
Leron, Uri. (1983). Structuring Mathematical Proofs. American Mathematical Monthly, Vol. 90, 3, 174-185.
Marinoff, L. (1994).
Mason, John. (1987). What do symbols represent? In Claude Janvier (Ed.) Problems of Representation in the Teaching and Learning of Mathematics. Hillsdale, NJ: Lawrence Erlbaum Associates.
Minsky, Marvin. (1987). The Society of Mind. New York: Simon & Schuster Inc.
National Council of Teachers of Mathematics (1991a). Curriculum and Evaluation Standards for School Mathematics. Reston, Va: NCTM.
National Council of Teachers of Mathematics (1991b). Professional Standards for Teaching Mathematics. Reston, Va: NCTM.
Nisbett, Richard. (1980). Human Inference: Strategies and Shortcoming of Social Judgment. Englewood Cliffs, NJ: Prentice-Hall.
Nisbett, Richard, Krantz, David, Jepson, C., & Kunda, Z. (1983). The Use of Statistical Heuristics in Everyday Inductive Reasoning. Psychological Review, 90 (4), pp. 339-363.
Noss, Richard & Hoyles, Celia. (1991). Logo and the Learning of Mathematics: Looking Back and Looking Forward. In Hoyles, Celia & Noss, Richard. (Eds.) Learning Mathematics and Logo. London: MIT Press.
Papert, Seymour. (1972). Teaching Children to be Mathematicians vs. Teaching About Mathematics. International Journal of Mathematics Education. Vol. 3.
Papert, Seymour. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
Papert, Seymour. (1991). Situating Constructionism. In Idit Harel & Seymour Papert (Eds.) Constructionism. Norwood, N.J. Ablex Publishing Corp. (Chapter 1).
Papert, Seymour. (1993). The Children's Machine. New York: Basic Books.
Phillips, J. (1988) How to Think About Statistics. New York: W.H. Freeman.
Piaget, Jean. (1952). The Origins of Intelligence in Children. New York: International University Press.
Piaget, Jean. (1975). The Origin of the Idea of Chance in Children. New York: Norton.
Poincar, Henri. (1912). Calcul des Probabilits.Paris: Gauthier-Villars.
Resnick, Mitchel. (1992). Beyond the Centralized Mindset: Explorations in Massively Parallel Microworlds. Doctoral dissertation, Cambridge, MA: Media Laboratory, MIT.
Resnick, Mitchel. (1991). Animal Simulations with *Logo: Massive Parallelism for the Masses. In J. Meyer & S. Wilson (Eds.), From animals to animats. Cambridge, MA: MIT Press.
Richmond, B. & Peterson, S. (1990). STELLA II. Hanover, NH: High Performance Systems, Inc.
Savage, Leonard. (1954). The Foundations of Statistics. New York: Wiley.
Scheffler, Israel. (1991). In Praise of the Cognitive Emotions. London: Routledge, Chapman and Hall.
Schoenfeld, Alan. (1991). On Mathematics as Sense-Making: An Informal Attack on the Unfortunate Divorce of Formal and Informal Mathematics. In Perkins, Segal, & Voss (Eds.) Informal Reasoning and Education.
Schwartz, Judah & Yerushalmy, Michal. (1987). The Geometric Supposer: an Intellectual Prosthesis for Making Conjectures. The College Mathematics Journal, 18 (1): 58-65.
Smith, John, diSessa, Andi, & Roschelle, Jeremy. (1994). Reconceiving Misconceptions: A Constructivist Analysis of Knowledge in Transition. Journal of the Learning Science, 3, pp. 115-163.
Soloway, Elliot. (1993). Should We Teach Students to Program? CACM, October 1993, 36(1).
Steinberger, M. (1994). Where does Programming fit in? Logo Update. Vol. 2 (3).
Suppes, Patrick. (1984). Probabilistic Metaphysics. Oxford, UK: Blackwell.
Surrey, Janet. (1991). Relationship and Empowerment. in Jordan, Judith, Kaplan, A., Miller, J.B., Stiver, I. & Surrey, Janet. Women's Growth in Connection: Writing from the Stone Center. New York: The Guilford Press.
Tierney, John. (1991). Behind Monty Hall's Doors: Puzzle, Debate and Answer? The New York Times National, July 21, 1991, page 1.
Thurston, William. (1994). On Proof and Progress in Mathematics. Bulletin of the American Mathematical Society. Volume 30, Number 2, April, 1994.
Turkle Sherry, & Papert, Seymour. (1991). Epistemological Pluralism and Revaluation of the Concrete. In Idit Harel & Seymour Papert (Eds.) Constructionism. Norwood N.J. Ablex Publishing Corp.
Tversky, Amos & Kahneman, Daniel. (1974). Judgment Under Uncertainty: Heuristics and Biases. Science, 185, pp. 1124Ü1131.
Tversky, Amos & Kahneman, Daniel. (1980). Causal Schemas in Judgments Under Uncertainty. In M. Fischbein (Ed.), Progress in Social Psychology. Hillsdale, NJ: Erlbaum.
Tversky, Amos & Kahneman, Daniel. (1983). Extensional vs. Intuitive Reasoning: The Conjunction Fallacy in Probability Judgment. Psychological Review, 90 (4), pp. 293-315.
Uspensky, James. (1937). Introduction to Mathematical Probability. New York: Prentice Hall.
von Glaserfeld, Ernst. (1987). Preliminaries to any Theory of Representation. In Claude Janvier (Eds.) Problems of Representation in Mathematics Learning and Problem Solving, Hillsdale, NJ: Erlbaum.
von Mises, Richard. (1964). Mathematical Theory of Probability and Statistics. New York: Academic Press.
von Mises, Richard. (1957). Probability, Statistics and Truth. New York: Dover Publications.
Wilensky, Uri. (1991). Abstract Meditations on the Concrete and Concrete Implications for Mathematics Education. In Idit Harel & Seymour Papert (Eds.) Constructionism. Norwood N.J.: Ablex Publishing Corp. Wilensky, Uri. (1993). Connected Mathematics: Building Concrete Relationships with Mathematical Knowledge.Doctoral dissertation, Cambridge, MA: Media Laboratory, MIT.
Wilensky, Uri. (forthcoming-a). GPCEE„an Extensible Microworld for Exploring Micro- and Macro- Views of Gases. Interactive Learning Environments Journal. Norwood, NJ: Ablex.
Wilensky, Uri. (forthcoming-b). Learning Probability through Building Computational Models. Proceedings of the Nineteenth International Conference on the Psychology of Mathematics Education. Recife, Brazil, July, 1995.
Wilensky, Uri. (in preparation). What is Normal Anyway? Therapy for Epistemological Anxiety.
[2] Assumptions implicit in the formulation of the paradox or in the preconceptions of the learner.
[3] A nice example of the many meanings of "derivative" can be found in a recent paper by Thurston (1994).
[4] Formal proof and definition is an after-the-fact reconstruction of the processes of coming to know in mathematics. The justification of such reconstruction for the purposes of communication within expert culture is certainly allowed. What is unfortunate and damaging pedagogoically is that this re-presentation becomes an active conception of what mathematics is and what it is to know mathematics.
[5] The taboo against expressing partial understandings is endemic to school discourse. To break it, teachers must explictly model expressing their own confusions and groping for clarity. One reason this is hard to do is that it is very difficult to remember what it was like not to grasp a mathematical concept that is now self evident. There are many striking parallels between the development of conservation in children (Piaget, 1952) and the acquistion of new mathematical concepts. One feature they share is the inconceivability of one's previous understanding-what is it like to think that there is more water in a tall glass than there was in the shorter glass which you emptied into the taller container? [for further discussion, see Wilensky, 1993].
[6] Because it suggests that making is endemic to mathematical activity, the Connected Mathematics view is that: learners make connections, they don't cross intellectual ravines. Thus the process of becoming expert in mathematics is one of adding connections and not removing or replacing novice knowledge.
[7] The shortest interview was two hours long, the longest eighteen hours and the median seven hours. These figures refer to the face-to-face interview time. Some interviews continued over electronic mail for up to two months following face-to-face interactions.
[8] Part of what makes an event singular is that we do not interpret it as a member of a class of events. It is only when we can stand at a distance from the event and see it in the context of many other events, that we can begin to make the reference classes needed to make probabilistic judgments.
[9] These "object-oriented" features of the language make StarLogo a more accessible environment for modeling. In contrast to other modeling environments, such as STELLA (Richmond & Peterson, 1990), which model with aggregate quantities and flows, StarLogo is "object" based - thus facilitating concrete interactions with the basic units of the model.
[10] The name "Bertrand's paradox" was given by Poincare.
[11] This was true in roughly half of the interviews in this study. The later in the interview the paradox occurred, the more likely that it was recognized and owned.
[12] A weaker form of this claim is that programming requires too much "overhead" that distracts learners from the mathematics at hand. This paper does not respond directly to this weaker claim. Let me note briefly that: 1) Logo and Starlogo are conceived here as lifelong tools and powerful expressive media across many domains, not just probability. 2) In contrast to languages such as Fortran or Basic, meaningful Starlogo programs are usually quite short and StarLogo has "low threshold" (i.e., easy for novices to write meaningful programs) as a primary language design criterion (Papert, 1980; Resnick, 1991).
[13] Or as some interviewees saw it, each process leads to a different "meaning" of random.
[14] A positivist or strict formalist critic might object that in fact the notion of randomness has been replaced by a more precise and technical notion. In practice, however, the new ideas coexist with the old and take much of their sustenance from their connections to prior conceptions and other contexts for recognizing randomness.
[15] The transcripts have been "cleaned up" some (removing pauses, umms and many interjections) for clarity of the exposition. Bracketed comments are the author's clarifying remarks.
[16] At this point, Ellie actually wrote down a formal mathematical proof by contradiction. The last line of the proof was: Therefore 2/3 = 3/4. Contradiction.
[17] The Starlogo procedures are divided into turtle procedures and observer procedures. Turtle procedures are executed by each turtle in parallel. Observer procedures set up the general environment and summarize the behavior of turtles.
[18] In this case, each turtle sets itself up at the origin on the circumference of a circle of radius 10.
[19] Ellie did go on and write the code to do this experiment just as a check of her insight. Her new code is the same as the old code except for a rewrite of the procedure "gen-random-chord".
[20] I chose not to intervene at this juncture and point out that the first experiment Ellie proposed did not correspond exactly to her first analysis and method of generating chords.