
|

|

|
Learning through
Participatory Simulations:
Network-based Design for Systems Learning in Classrooms
Uri Wilensky1
Walter Stroup
Proceedings of CSCL '99, Computer-Supported Collaborative Learning, Stanford University
A modified version of this paper was presented at the Annual meeting of the American Education Research Association, April, 1999, Montreal, Canada| Uri Wilensky | Walter Stroup |
| Center for Connected Learning | Department of Curriculum and Instruction |
| Northwestern University | The University of Texas at Austin |
| Annenberg Hall 311 | Austin TX 78712-1294 |
| 2120 Campus Drive | wstroup@mail.utexas.edu |
| Evanston, IL 60208 | 512-232-3958 |
| uriw@media.mit.edu | |
| 847-467-3818 |

|

|

|
Abstract:
This project brings together two lines of research—the study of complex dynamic systems and the use of participatory simulations as a powerful way into systems modeling—both of which can be enabled and advanced through emerging network technologies. The study of dynamic systems stands as a new form of literacy for all.. Participatory Simulations Activities can support new forms of classroom interaction and can serve to catalyze the engagement with dynamic systems modeling as a core feature of the education of all students. To accomplish these goals, we introduce a new architecture, HubNet. HubNet is an open client-server architecture, which enables many users at the "Nodes" (currently TI graphing calculators) to control the behavior of individual objects or agents and to view the aggregated results on a central computer known as the Hub. This network of nodes is integrated with a powerful suite of modeling, analysis and display tools that together give both the capacity to "fly’ the system in intuitive mode, to reflect on the emergent result of their simulation and, also, to encode their strategies as rules which the system can then run independently. The HubNet system is being used in several middle and secondary classrooms. An illustrative example of classroom use is presented.
Keywords: modeling, simulation, math education, science education, collaboration, graphing calculators, systems thinking, complex systems, computer-supported collaboration, emergent phenomena
1.0 Introduction
In this paper, we introduce and describe a new network-based architecture, HubNet, designed for enabling students to engage in participatory simulations of complex dynamic systems. Working together with a commercial partner, we are engaged in an iterative design and test cycle to refine the HubNet system and its associated activities. Early versions of HubNet are in use in classrooms in Boston, Ma and Austin Texas. This work is being undertaken under the auspices of the Participatory Simulations Project (PSP) – an NSF-funded collaboration between Tufts University’s Center for Connected Learning and The University of Texas at Austin.
In the following sections of this paper, introduce our project and give an example of its use in school settings. We begin with a brief history of the use of participatory simulations in math/science education, move on to describing the HubNet architecture and an illustrative classroom activity, then outline future directions of the Participatory Simulations Project.
2.0 What’s a Participatory Simulation?
Students engaged in participatory simulations act out the roles of individual system elements and then see how the behavior of the system as a whole can emerge from these individual behaviors.
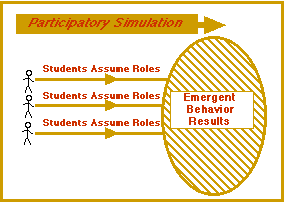
Figure 1: In a Participatory Simulation Students Assume Roles in a Simulation and an Emergent Behavior Results.
The emergent behavior (see Figure 1) of the system and its relation to individual participant actions and strategies can then become the object of collective discussion and analysis.
While such participatory role-playing activities have been commonly used in social studies classrooms, they have been infrequently used in science and mathematics classrooms. Our use of the term participatory simulations is intended to refer to such role-playing activities aimed at exploring how complex dynamic systems evolve over time. Our focus is primarily on learning in science and mathematics classrooms . For example, each class member could play the role of a predator or prey in an ecology and engage in a classwide discussion of the resultant global population dynamics. A wide ranging set of sample content areas for participatory simulations include the spread of a disease, the flow of traffic in a grid, the distribution of goods in an inventory system, the diffusion of molecules through a membrane, or the emergence of an algebraic function from a set of points
For us, a participatory simulation or emergent activity must draw attention to systems dynamics and systems learning. This attention to dynamic structure, evolving state, feedback, and the like is not so much a feature of the activity itself as it is in the focusing of one’s sense-making on the systems aspects the experience. Drawing attention to systems dynamics and systems learning describes the quality of our relationship to a participatory experience. Using this constraint on what we mean by a participatory simulation – that attention must be drawn to systems dynamics and systems thinking – we can now track a history of the development of participatory simulations.
3.0 Why do Participatory Simulations and Emergent Activities Matter?
A core commitment of this Project is to research the use of participatory simulations as a way into systems dynamics and complexity learning for ALL students. During recent decades, there has been a recognition of the importance of understanding the behavior of dynamic systems—how systems of many interacting elements change and evolve over time and how global phenomena can arise from local interactions of these elements. New research projects on chaos, self-organization, adaptive systems, nonlinear dynamics, and artificial life are all part of this growing interest in systems dynamics. The interest has spread from the scientific community to popular culture, with the publication of general-interest books about research into dynamic systems (e.g., Gleick, 1987; Waldrop, 1992; Gell-Mann, 1994; Kelly, 1994; Roetzheim, 1994; Holland, 1995; Kauffman, 1995).
Research into dynamic systems touches on some of the deepest issues in science and philosophy—order vs. chaos, randomness vs. determinacy, analysis vs. synthesis. At the same time, this new field has introduced new objects of study—objects that were barely conceivable before the development of systems analysis tools and barely renderable without computational media. These new media allow us to analyze not just laboratory-based phenomena but also connect strongly to many patterns and phenomena found in the everyday world. The problems our society faces are increasingly systemic in character. The perspective of complex systems is rapidly infiltrating all areas of natural and social sciences and is increasingly needed to make progress with these problems.
It is the stance of the PSP that the study of dynamic systems is not just a new research tool or new area of study for scientists. Our stance is that the study of dynamic systems stands as a new form of literacy for all, a new way of describing, viewing, and symbolizing phenomena in the world. The language of the present mathematics and science curriculum employs static representations. Yet, our world is, of course, constantly changing. This disjunct between the world of dynamic experience and the world of static school representations stands as one source of student alienation from the current curriculum (Chen & Stroup 1994; Stroup, 1994; Wilensky, 1993; Wilensky & Reisman, 1998).
Research in mathematics/science education and cognitive science (Mandianch & Thorpe, 1987; Mandinach & Cline, 1994; Tversky & Kahneman, 1974) has documented that students have considerable difficulties in making sense of complex systems. In particular, Resnick and Wilensky have documented the considerable difficulties people have in making sense of emergent phenomena, global patterns that arise from distributed interactions, central to the study of complex systems. This constellation of difficulties in understanding emergent phenomena and constructing distributed explanations of such phenomena has been labeled the "deterministic/centralized mindset" (Resnick & Wilensky, 1993; Wilensky & Resnick, 1995, 1999; Resnick, 1996). Our aim in the PSP and in developing the HubNet system is to be catalytic in helping secondary and post-secondary students move beyond the deterministic/dentralized mindset and advance their understanding of complex dynamic systems. We view the facility with systems thinking, modeling and emergence as a new and necessary form of literacy for our citizenry.
The theoretical and computer-based tools arising out of the study of dynamic systems can describe and display the changing phenomena of science and the everyday world. A core conjecture of the PSP is that the affordances of participatory simulations, as supported by networked modeling and analyses tools discussed below, provide a powerful way into systems related sense-making that can help realize the vision of systems learning for all students.
4.0 What’s New in the Participatory Simulations Project?
The list of what is new about the PSP includes the development and use of innovative networked classroom-based technologies to connect learners’ evolving intuitions with powerful tools for modeling and analysis; and the pursuit of fundamental research into emergent learning through the use of network-based interactivity. Comparing Figure 2 below with Figure 1 shown earlier, these innovations are represented by the double-headed arrow connecting learner intuitions with tools of analysis and modeling. These advances are to be supported by new fundamental research into emergent learning and by developing an innovative, networked technological substrate in close collaboration with a commercial partner, Texas Instruments.
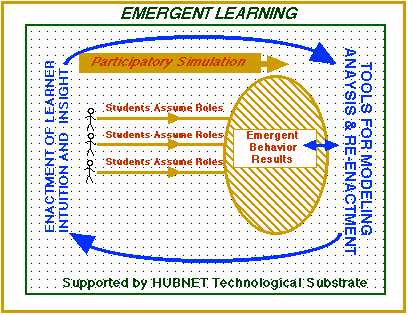
Figure 2. What’s new in this project is the use of an innovative technological substrate (HubNet) to support emergent learning based on the iterative interaction of student insights and tools for modeling analysis and re-enactment.
As Figure 2 suggests, by interconnecting the analyzable artifacts created from learner activity with powerful tools of analysis and modeling the enactive aspects of participatory simulations stand to be deepened and extended. Additionally, learners working in the networked environment make overt and visible their strategies in relation to generating different kinds of emergent behavior. In so doing, these strategies become increasingly well-articulated and refined in ways that scaffold both learner understanding of dynamic systems and the actual use by learners of the tools themselves. Through the participation in and analysis of emergent activities, we expect learners to come to see the tools as increasingly useful in helping them to further articulate their insights into the emergent behavior of dynamic systems. These tools enable them to analytically understand these systems, in effect working with the mathematics of change without needing to master the formalisms of differential equations. From the research side of the PSP, the network-based activity will help to make visible learners’ ideas and ways of organizing their experiences, which should significantly advance our understanding of these forms of emergent learning.
5.0 A Brief History of Participatory Simulations
The first major instance of which we are aware where a participatory simulation was used in the context of systems dynamics and systems learning was The Beer Game as developed by Jay Forrester and his systems dynamics group at MIT in the early 1960’s. There is a significant literature related to The Beer Game and interest in this participatory simulation has been recently revitalized as a result of its appearance in Senge’s widely read The Fifth Discipline (1990). The game does much to highlight the ways in which costly unintended behaviors of a system (in this case beer inventory in a distribution system) can emerge from participants attempting to act rationally in their localized role (e.g., as beer retailer, wholesaler, distributor, or producer). A number of other such PSA were developed at this time. One popular PSA, FishBanks (Meadows, 1986) was developed by Meadows as an "interactive, role-playing simulation in which groups are asked to manage a fishing company." Students try to maximize their assets in a world with renewable natural resources and economic competition.
More recently, new classes of so-called "object-based" simulation activities have been developed (Resnick & Wilensky, 1993; 1998; Wilensky & Resnick, 1995). In these so-called "StarPeople" activities, participants typically play the role of "ants" in an anthill simulation, moving around the room and exchanging "messages." After participating in these StarPeople activities students observe the emergence of global patterns from their local interactions. These pattern become the objects of reflection and discussion.
6.0 Participatory Simulations Activities and Computational Tools
Throughout much of the fifty-year history of participatory simulations computational technologies have played a central role. The systems dynamics group at MIT developed a class of computational "flight simulators" to be used by individuals and groups of managers to gain experience flying a complex dynamic system like a modern business. More recently, multi-player networked versions of the beer game have been implemented (Coakley et al, 1995) and it is now even possible to immerse oneself in a multi-player versions of the game on the internet (Powersim Corporation, 1998). Management trainers have argued that there is a need for a tighter coupling between computer simulations and user experience. In possibly the first known use of the term participatory simulations, Diehl (1990) constructed systems that gave users more control over and participation within the simulations by allowing users to input more real word decisions and view output of familiar reports. These simulations were modelled using finite-difference tools like STELLA
In contrast to the "aggregate" finite-difference computer modeling tools used to analyze simulations like The Beer Game, these simulation activities have been designed to be further explored using object-based parallel computer modeling languages (OBPML) such as StarLogo and StarLogoT (Resnick, 1994; Wilensky, 1995; 1997b). Borovoy, Colella and fellow researchers at MIT (Colella et al, 1998; Borovoy et al , 1996; 1998) have developed wearable computational badges (or "thinking tags") that allow users to move freely while communicating information between badges. Colella (1998) developed, implemented and researched student learning with one of the first instances of a participatory simulation supported by a thin layer of computing technology. Disease propagation models are natural candidates for this kind of participatory simulation and have been implemented by a number of researchers and curriculum developers (Colella et al, 1998; Stor & Briggs, 1998).
A significant innovation in this project is a commitment to exploring the complementarity of these two fundamental kinds of dynamical systems modeling – aggregate and object-based approaches. This compels a careful attention to a) the relationships between macro- and micro-levels of understanding a system (Chen & Stroup, 1994; Wilensky, 1993; in press); b) thinking in levels (Wilensky and Resnick, 1999); c) systems thinking (Chen & Stroup, 1994); and d) the analysis of systems like gases (Wilensky, 1994; Wilensky, 1999; Wilensky, Hazzard, and Froemke, 1999). Through the use of participatory simulations and attention to the kinds of constructs learners articulate and extend in relation to both the aggregate and object-based modeling environment, we expect to gain deeper insights into how these kinds of distinct but inter-related forms of analyses interact and complete one another.
6.1 The Gap between PSA and Computational Technologies
Despite this rich history of participatory simulation activities and the existence of powerful modeling and analysis tools, by and large, PS activities have not made their way into the science and mathematics curriculum. While there are several reasons for this neglect, a major factor is the lack of close integration of the PS activities with modeling/analysis technologies. Once the PS activity has been enacted in the classroom, the major vehicle for benefiting from this activity is classroom discussion. The simulation cannot be replayed, subjected to alternative scenarios and assumptions, presented through different graphing lenses or analyzed with statistical tools. This limits the powerful learning about systems that is potentially available.
A goal of the PSP project and the HubNet architecture is to fully address this gap and connect PSA with powerful computational tools. Furthermore we want to ensure that access to these tools and experiences to the widest possible student population. For this reason in developing the HubNet architecture we partnered with Texas Instruments to enable HubNet to run on standard graphing calculators such as the TI-83 and its successors. There is a very large installed base of graphing calculators in secondary schools and the HubNet architecture allows these to be leveraged (with a relatively small incremental cost) for substantial explorations of PSA in the majority of classrooms.
A potential barrier to wide-spread adoption of networked activities is the difficulties in authoring new PSA. Our Java-based development effort of N-Logo extends the object-based modeling capabilities of StarLogoT by having the N-Logo language also serve as a scripting language for the creation of HubNet-based participatory simulations. Just as object-based models are extensible (Wilensky, 1997a, 1999), the network-based emergent activities created in N-Logo will be extensible.
Absent the support provided by the network, the processes associated with implementing a given participatory simulation can prove sufficiently cumbersome so as to present a real barrier to its successful implementation in classrooms. For example, the beer game simulation, like most of the simulations developed by systems dynamics groups, relies on participants relaying their decisions through paper and pencil messages that propagate through the gaming "system." This laborious, repetitive and error-prone process "begs" for a computer-based implementation to free the participants to focus on the consequences of their decisions and strategies. Similarly, for object-based participatory simulations, the role-playing and computer-based modeling can shed light on each other but they cannot share data or interact dynamically. The role-play cannot be saved, re-analyzed, or compared with other role-plays except through a laborious hand-coded process.
7.0 What is HubNet?
HubNet is the name we have given to a new architecture we have designed to give students the experience of participating as elements in a simulation of a complex dynamic system. HubNet is an open client-server architecture, which enables many users at the "Nodes" to control the behavior of individual objects or agents and to view the aggregated results on a central computer known as the "Hub". This network of nodes is integrated with a powerful suite of modeling, analysis and display tools that, together, give the capacity to "fly" the system in intuitive mode, to reflect on the emergent result of the simulation and to encode student strategies as rules which the system can then run independently.


Figure 3.Students engaged in participatory simulation supported by HubNet calculator network. On the left each student sees her/his own calculator view. On the right is the projected classroom display of the emergent result.
The HubNet architecture is being developed in stages. At present, a workable minimal subset of functionality is implemented. This subset consists of 1) a suite of networked graphing calculators called Classnet (or HubCalc) developed in concert with our commercial partner, Texas Instruments. 2) a server, which talks to the Classnet network and 3) an object-based parallel modeling language, N-Logo, which is an enhanced port of the StarLogoT language that enables users to build object-based models of systems consisting of thousands of distributed elements. We call this three-component HubNet sub-system ClassLogo. Future versions of HubNet will integrate aggregate modeling languages, such as STELLA, facilitating a dialogue between object-based and aggregate approaches. Many more analysis and display tools will also be integrated (through the ESCOT Project (Kaput & Roschelle, 1998) and through internal development) as well as hooks allowing a much wider array of node hardware including arbitrary Internet hosts.
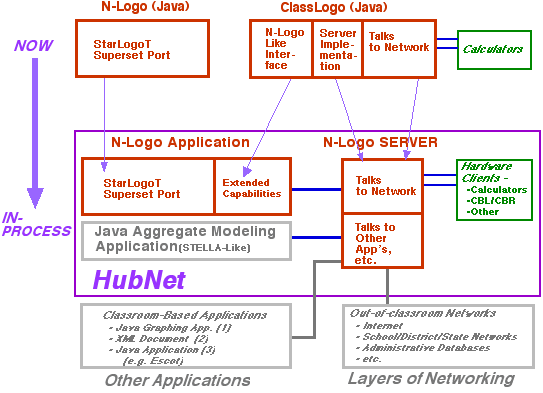
Figure 4: The HubNet Architecture: Now and in the Future
HubNet is designed with the assumption that the nodes have significant resident functionality (at least that of a programmable graphing calculator). The network layer implements flexible communication protocols that include the ability to upload and download data sets, upload and download program (e.g., applets), monitor key-presses at the hand-held level, support real-time interaction as in network computer games, and form collaborative groups of various sizes (e.g., peer to peer, small groups, and whole class modes). The HubNet hardware includes an up-front computer (the "hub") capable of addressing the network of nodes and a display capability (e.g., a projection system) that enables an entire class to view the simulation.
As described earlier, the current working subset of HubNet, ClassLogo, uses the prototype TI Classnet system (2) consisting of a suite of networked graphing calculators. The resident functionality of the calculator, including capabilities of interacting with real world devices such as sensors and motors, CBLs and CBRs, allows for a wide range of PSA to be implemented in the classroom.
ClassNet supports fully networked modes of interaction with and among learners. While synchronization between the data on the hand-helds and the Hub is supported in this model, the model can also support on-going, real-time interactivity and exchange. This fully-networked HubNet system in intended to support a range of different topologies for collaboration among learners including point-to-point, small group and whole class interaction. This more inclusive range of interactivity and collaboration cannot be supported in models based exclusively on the synchronization model.
8.0 HubNet in the Classroom – An introductory example
Participatory simulations stand to introduce fundamentally new and significant forms of reasoning and insight to school-based curricula. They also have the potential to be transformative of students’ experience and understanding of the topics at the core of the traditional curriculum. We present here an elementary example of an activity well connected to the current curriculum that illustrates this potential — the Function Activity. The Function Activity has already been used in a number of different settings including both an urban middle school and an urban high school. The Function Activity sequence begins with a seemingly random collection of points visible on the up-front projection system (see Figure 5a). The teacher begins the conversation by asking students if there is any pattern in this collection of points. Although students will occasionally qualify their comments with the observation that there "might" be a pattern, the general consensus is that there is not an obvious pattern. The teacher then "hands out" one of these points to each of the students using the network. A single point is then visible on each student’s screen (5b). The student finds the location of the point by moving the calculator cursor, the "+" shown in Figure 5b, to the point and reading off its x and y-coordinate. The teacher now gives the class a rule by which to move their individual points.
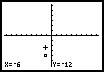
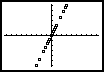
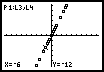
5a 5b 5c 5d
Figure 5: The Function Activity sequence for the rule, "move until
your y-value is two times your x-value."
The rule illustrated in Figure 5c is, "move until your y-value is two-times your x-value." When the students have found this location for their particular point, they press ENTER on the calculator and the network software collects the points. Either before or after the students move their individual points, the question can be asked, "What do you think will happen if we now display all the points together?" Students will give a range of answers, such as "a ‘V’ will form", or "some kind of line." Teachers can ask the students to explain why they made these predictions. Initially students will usually say something like "I just guessed" or "it is a hunch". The teacher can then display the results. Figure 5c illustrates what appears if every student follows this rule.
Every time this activity has been run in a classroom, we have observed that students are quite invested in locating their individual points. Initially, there have been a significant number of points "off the line". If a particular student realizes that his or her point is "off" the emergent pattern, s/he will sometimes offer an explanation for what happened. What is encouraging to hear and observe in the video-tapes of the classroom interactions is that consistently students are willing to try and make sense of other students’ reasoning. Even for points off the line, students will say something like "oh, that person must have just switched his y and his x," or "she didn’t multiply by the negative." Rather than simply ridicule "wrong" answers, students will assume their colleagues had a reason for what they did and that they can identify with these other forms of reasoning. One hears comments like, "I almost did that but.…" The classroom discussion for both students and teachers centers more on the reasoning the learners brought to the task, and less on "right" or "wrong". Both the teacher and the students have a "snapshot" of how the entire class’s reasoning is working. The teacher can help shape the spontaneously generated conversations that occur.
Figure 5d illustrates the power of carrying out these kinds of activities on top of devices – in this case, graphing calculators – that have significant resident functionality. Using the network, the collection of points can be handed out to all of the students. The TRACE feature of the calculator allows the teacher or students to jump from point to point and read off the values. Students can use this feature to locate "their point" in collection. Some of the points start off with the same x value and different y values, so some of the points that were separately visible at the beginning are on top of one another after following a rule like "move until your y value is two times your x value." The students will notice this by observing that there appear to be fewer points after the activity than there were beforehand. Later they realize that all the points are still "there" but that some of them are now on top of each other. Students will ask, "What happened to the other points?" Using the TRACE feature students can find themselves but will still ask what happened to some of the others. "They’re on top of each other," answered one boy in a high school class, but he wasn’t sure why this would happen. A subtle aspect of the idea of function is raised. A well-defined function must be one-to-one (injective) but is not necessarily on-to (surjective).
The functionality of the calculators can also be used to explore the notation that is used for these kind of function-rule situations. Each student can have the emergent collection of points sent to his or her own calculator. The teacher can then ask the students to plot five (traditionally notated, continuous) functions that go through these points. Not only might students generate the function Y=2X, but in generating other functions that go through these points they can also immediately start to make sense of equivalence in a way that is all but lacking in traditional approaches to "simplifying functions". (3)
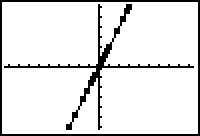
Figure 6: Using the "burned-in" capability of the graphing calculator to explore what analytic function(s) might go through the points created by following the given rule.
Other function rules have been explored using this sequence (e.g. move until your y value is five more than your x value or move until your y value is the absolute value of your x value). In each case students are asked to predict before hand what pattern might emerge. The link from the rule they used to move their own embodied point to the analytic function can be explored. By using this participatory approach, cognitive scaffolding is provided for moving from "my point" to big ideas related to the concept of a function and to various analytic forms of expressing the functional dependency.
9.0 Future Directions
As indicated above, the HubNet architecture is in a preliminary stage. Significant project resources are allocated to developing HubNet and completing the fully networked architecture. Alongside this iterative design research, we will continue to conduct both implementation and curricular research with successive versions of HubNet. We have begun to design and test a set of PSA using ClassLogo that make use of sophisticated new content domains. This fundamental research is being carried out in economically challenged inner-city schools. Significant resources from the PSP Project are going toward site-based support and innovation. We are working alongside the teachers in targeting and implementing network-based participatory simulations that can transform students’ understanding of core concepts of the current curriculum (e.g. the concept of function) even as fundamentally new systems-understandings and content areas are introduced.
In this context, we seek to gain a better understanding of how a PSA can significantly advance student understanding of the unfolding dynamics of systems. We hope to shed light on how learners' intuitive understandings and ways of responding interact with rule-based, embodied (e.g., StarLogoT, N-Logo) and aggregate (e.g., STELLA) modeling environments. Through this design, implementation and curricular research, we hope to further the goal of advancing systems related understanding for all students.
Acknowledgements
The preparation of this paper was supported by the National Science Foundation (Grants REC-9814682, REC-9632612), The ideas expressed here do not necessarily reflect the positions of the supporting agency. A longer version of this paper was presented at the Annual Meeting of the American Education Research Association, in April 1999. Chuck Shubert, Eamon Mckenzie and Geoff Hulette of Tufts CCL have been major contributors to N-Logo, ClassLogo and the HubNet software. The Classnet team at Texas Instruments are largely responsible for the HubNet hardware. Sarah Davis and Ed Hazzard have developed many HubNet activities and flown them in their classrooms. James Early and Yolanda Martinez have used some of the activities in their classrooms. Andy Begel, Rob Froemke, Eamon McKenzie, Mitch Resnick and Brian Silverman played significant roles in the development of the StarLogoT modeling language. We are grateful to Ed Hazzard for constructive feedback on drafts of this paper.
Footnotes
References
Borovoy, R., McDonald, M., Martin, F., & Resnick, M. (1996). Things that Blink: Computationally Augmented Name Tags. IBM Systems Journal, 35(3).
Borovoy, R. Martin, F. Vemuri, S. Resnick, M. Silverman, B & Hancock, C. (1998). Meme Tags and Community Mirrors: Moving from Conferences to Collaboration. Proceedings of the 1998 ACM Conference on Computer Supported Collaborative Work.
Chen, D., & Stroup, W. (1993). General Systems Theory: Toward a conceptual framework for science and technology education for all. Journal for Science Education and Technology.
Coakley, James. R., John A. Drexler, Anna E. Kircher, and Erik W. Larson. "Using Simulation Methods to Implement Multi-Person Role-Playing Board Games". submitted to Journal of Management Education , Jun 95. Return in Aug 95 for revision. http://www.bus.orst.edu/faculty/coakley/beergame.htm
(no longer available)Colella, V., Borovoy, R., and Resnick, M. (1998) Participatory Simulations: Using Computational Objects to Learn about Dynamic Systems. Proceedings of the Computer Human Interface (CHI) '98 conference, Los Angeles, April 1998.
Diehl, E. (1990). Participatory Simulation Software for Managers: The Design Philosophy behind MicroWorlds Creator. European Journal of Operations Research 59 (1): 203-209.
Forrester, J. W. (1968). Principles of Systems. Norwalk, CT: Productivity Press.
Gell-Mann, M. (1994). The Quark and the Jaguar. New York: W.H. Freeman.
Giodan, A. (1991). The importance of modeling in the teaching and popularization of science. Trends in Science Education, 41(4).
Gleick, J. (1987). Chaos. New York: Viking Penguin.
Holland, J. (1995). Hidden order: How adaptation builds complexity. Helix Books/Addison-Wesley.
Jackson, S., Stratford, S., Krajcik, J., & Soloway, E. (1996). A learner-centered tool for students building models. Communications of the ACM, 39(4), 48-49.
Kaput, J. & Roschelle, J. (1998). ESCOT Project. http://wise.sri.com/escot/home.html.
Kauffman, S. (1995). At home in the universe: The search for the laws of self-organization and complexity. Oxford: Oxford University Press..
Mandinach, E. B., & Thorpe, E. T. (1987). The systems thinking and curriculum innovation project: Technical report, part 1. (TR-87). Educational Technology Center. Harvard Graduate School of Education. Nichols House, Appian Way. Cambridge MA 02138.
Mandinach, E. B., & Cline, H. F. (1994). Classroom dynamics: Implementing a technology-based learning environment. Hillsdale, NJ: Lawrence Erlbaum Associates
Meadows, D. (1986). Fish Banks, LTD. In Durham, NH: Institute for Policy and Social Science Research. http://www.unh.edu/ipssr/index.html/ipssr/lab/fishbank.html
Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. New York: Basic Books.
Pea, R., Edelson. D., & Gomez, L. M. (1994). Distributed collaborative science learning using scientific visualization and wideband telecommunications. Paper presented at the 160th. meeting of the American Association for the Advancement of Science.
Powersim Corporation (1998). http://www.powersim.no/demo/WebSims/Beergame/index.htm
Prigogine, I., & Stengers, I. (1984). Order out of chaos: Man’s new dialogue with nature. New York: Bantam Books.
Resnick, M. (1994). Turtles, termites and traffic jams. Explorations in massively parallel microworlds. Cambridge, MA: MIT Press.
Resnick, M., & Wilensky, U. (1998). Diving into complexity: Developing probabilistic decentralized thinking through role-playing activities. Journal of the Learning Sciences, 7(2), 153-171.
Resnick, M., & Wilensky, U. (1993). Beyond the deterministic, centralized mindsets: New thinking for new sciences. Presented at the annual conference of the American Educational Research Association, Atlanta, GA.
Richmond, B., & Peterson, S. (1990). Stella II. Hanover, NH: High Performance Systems, Inc.
Roberts, N. (1978). Teaching dynamic feedback systems thinking: an elementary view. Management Science, 24(8), 836-843.
Roberts, N., Anderson, D., Deal, R., Garet, M., & Shaffer, W. (1983). Introduction to computer simulations: A systems dynamics modeling approach. Reading, MA: Addison Wesley.
Senge, P. (1990). The Fifth Discipline. New York: Doubleday/Currency.
Smith, D. C., Cypher, A., & Spohrer, J. (1994). Kidsim: Programming agents without a programming language. Communications of the ACM, 37(7), 55-67.
Stor, M. & Briggs, W. (1998). Dice and disease in the classroom. The Mathematics Teacher, v. 91, no. 6. Pp 464-468.
Stroup, W. (1995). Dynamics and calculus for the young learner. Teacher’s Lab, 16-18.
Stroup, W. (1993). What the development of non-universal understanding looks like: Results from a qualitattive calculus assessment. Technical Report. Educational Technology Center. Harvard Graduate School of Education. Cambridge, MA.
Stroup, W. (1996). Embodying nominalist constructivism: Making graphical sense of learning the calculus of how much and how fast. Doctoral Dissertation. Harvard Graduate School of Education. Cambridge, MA.
Stroup, W. (1998). The Root Beer Game.
Tversky, A., & Kahneman, D. (1974). Judgment under uncertainty: Heuristics and biases. Science, 185, 1124–1131.
Waldrop, M. (1992). Complexity: The emerging order at the edge od order and chaos. New York: Simon & Schuster.
Wilensky, U. (1999). GasLab—an extensible modeling toolkit for exploring micro- and macro- views of gases. In N. Roberts, W. Feurzeig, & B. Hunter (Eds.), Computer modeling and simulation in science education. Berlin: Springer Verlag.
Wilensky, U., Hazzard, E & Froemke, R. (1999). An Extensible Modeling Toolkit for Exploring Statistical Mechanics Proceedings of the Seventh European Logo Conference - EUROLOGO'99, Sofia, Bulgaria.
Wilensky, U. & Resnick, M. (1999). Thinking in Levels: A Dynamic Systems Perspective to Making Sense of the World. Journal of Science Education and Technology. Vol. 8 No. 1.
Wilensky, U. & Reisman, K. (1998). Learning Biology through Constructing and Testing Computational Theories -- an Embodied Modeling Approach. In Y. Bar-Yam (Ed.), Proceedings of the Second International Conference on Complex Systems. Nashua, NH: New England Complex Systems Institute.
Wilensky, U. (1997a). What is normal anyway? Therapy for epistemological anxiety. Educational Studies in Mathematics. Special Edition on Computational Environments in Mathematics Education. Noss R. (Ed.) 33(2), 171-202
Wilensky, U. (1997b). StarLogoT. /cm/StarLogoT/
Wilensky, U. (1996). Modeling Rugby: Kick first, generalize later? International Journal of Computers for Mathematical Learning. 1(1).
Wilensky, U. (1995). Paradox, programming and learning probability: A case study in a connected mathematics framework. Journal of Mathematical Behavior, 14(2).
Wilensky, U. & Resnick, M. (1995). New thinking for New Sciences: Constructionist approaches for exploring complexity. Presented at the annual conference of the American Educational Research Association, San Francisco, CA.
Wilensky, U. (1994). GasLab. /cm/models/gaslab/
Wilensky, U. (1993). Connected Mathematics: Building concrete relationships with mathematical knowledge. Doctoral dissertation, Cambridge, MA: Media Laboratory, MIT.
Wilensky, U. (1991). Abstract meditations on the concrete and concrete implications for mathematics education. In I. Harel & S. Papert (Eds.), Constructionism. Norwood NJ.: Ablex Publishing Corp.