 |
 |
 |
|
Chris Westbury |
Uri Wilensky |
 |
 |
 |
Defining cognitive science is surprisingly difficult. As one recent commentator has written "Most people know what cognitive science is when they see it; they have far more difficulty providing a strict definition" (Keil, 1998, p. 354). The definitional difficulty may be attributed to several factors. In part it springs from the fact that cognitive science arose from a intermingling of several different academic disciplines, and thus encompasses a wider range of intellectual territory than other academic disciplines. In part the difficulty in defining cognitive science arises from the dynamic nature of the discipline itself. Science has progressed rapidly in the four decades since cognitive science first appeared. As a result of this rapid progress, the definitional utility of some of the original central features of the discipline have been rendered doubtful, and several features which were originally under-appreciated or simply ignored have come to play a central role in current theorizing.
The definitional difficulty springs largely from the inherent complexity of the subject matter. The study of cognition admits of multiple levels of analysis which interact in a myriad of ways, allowing for many apparently different approaches to coexist under the same rubric- so that, for example, social psychologists and neuropsychologists working in the same department may both consider themselves to be cognitive psychologists without ever finding a common explanatory vocabulary. A person tempted to give a concise definition of the discipline in a few words risks misrepresenting cognitive science. In this section cognitive science will be defined in a broad way, by placing it in a historical framework (in the first subsection) and by outlining a number of attributes which may be considered to be of particular current importance (in the second subsection).
The decision about where to begin with a history of cognitive science must be made somewhat arbitrarily. It is possible to trace the roots of cognitive science back many centuries: one could reasonably argue that cognitive science cannot be understood without being situated in the tradition of Western thinking which goes back at least to Aristotle. Instead of starting so early, one could opt to begin a history more recently by pointing out the strong methodological parallels between cognitive science and the psychophysics which characterized early scientific psychology for a brief period in the late 1800s and early 1900s. Ignoring an even greater portion of the past, one might reasonably trace many of the ideas of cognitive science to the emergence of cybernetics (literally, "the science of steering"), which was launched with the appearance of Norbert Weiner’s (1948) book Cybernetics: or Control And Communication in the Animal and The Machine. One might also choose to ignore its precursors altogether and begin telling the history of cognitive science with the earliest form which is continuous in an unbroken chain with its current form. It is this last option which will be pursued here.
There is widespread agreement among those who have written on the history of cognitive science that the discipline as it is now practiced arose in the half decade between 1955 and 1960 (Gardner, 1985). One commentator who was a participant in the original activities which gave rise to the discipline has even argued that the birth of cognitive science may be plausibly pinned down to a precise day: September 11, 1956 (Miller, 1979; see also Breuer, 1993). On that day a symposium on the topic of information science was held at the Massachusetts Institute For Technology (MIT) in Boston. Although it was not the first meeting devoted to the topic of information science, the MIT symposium brought together for the first time a number of thinkers from various disciplines who were to play important roles in the emergence of cognitive science.
Information theory was, along with computer science, one of the two related disciplines underlying cognitive science which were strongly spurred on by the practical challenges posed by the Second World War. The British and American governments wanted to improve their understanding of how communicated information could be coded, decoded, comprehended, and otherwise manipulated. They gave heavy funding to disciplines which might lead to practical breakthroughs in these areas.
In England, the result was the development by Colin Cherry and Donald Broadbent of a new metaphor for understanding human beings: the information processing metaphor. Cherry and Broadbent proposed that we view human beings as information processing devices, and that we describe them in the same terms as were being used to describe simpler information processing devices, as a set of input and output channels with known, limited capacities (Broadbent, 1958). This metaphor led to the development of a new and fruitful research program dedicated to exploring the constraints and functioning of human sensory channels, thereby allowing for an unambiguous means of stating and exploring an old idea in which scientific progress was making increasingly thinkable: that the human being might be a kind of complex machine. One of the most well-known talks delivered at the MIT conference presented a finding that remains to this day perhaps the most well-known finding of the information processing paradigm: George Miller’s discovery that short-term memory was limited to roughly seven items (Miller, 1956) In the United States, the demands of war led to the development of ENIAC, the first electronic computer, which had been designed for computing weapons trajectories. ENIAC was switched on in 1946, a little too late to help the war effort. Its design was directly based on theoretical principles outlined in a famous paper published in 1936 by the British mathematician Alan Turing, and in a MIT master’s thesis published in 1938 by the mathematician, Claude Shannon. Turing had proven that there was a simple, general form underlying all possible algorithmic computations: a universal language for describing computation. Shannon built on this work by demonstrating that the functions of existent electronic relays and switches were sufficient to implement a machine which could simulate1 the universal computing device that Turing’s paper had described.
An American mathematician named John Von Neumann was closely following the developments in the emerging field of electronic calculation. He contributed so many important conceptual breakthroughs to the organization of the computer hardware that the modern computer architecture is often referred to as ‘the Von Neumann architecture’. Von Neumann was also among the first to speculate on the connection between the new technology and the human brain. He died of cancer before seeing the publication of his contribution to the developing field of cognitive science: his book, The Computer And The Brain (Von Neumann, 1958).
One of the talks given at the 1956 MIT symposium, given by Alan Newell and Herbert Simon, built on Von Neumann’s dream of trying to understand human thinking in terms of the electronic computer. Newell and Simon presented the first complete proof of a theorem in symbolic logic ever generated by machine, using a computer which was named ‘Johnniac’ in honor of Von Neumann. In some ways the presentation was a mere formality, since Simon had proven by hand some months earlier that such a demonstration was in principle possible, and since the theorem the computer proved had already been proven true decades earlier by Whitehead and Russell. Nevertheless, Newell and Simon’s demonstration marked the beginning of a new age. It was not just that dead machinery was exhibiting its nascent intelligence. Newell and Simon insisted that they were not merely demonstrating machine intelligence, but actually demonstrating the general laws underlying all thinking (Simon, 1962). In their insistence on this interpretation, they stated a major claim of early cognitive science: that one could study the general organization of cognitive processing independently of how those processes were implemented in the human brain. There was a dissociation between the algorithm used to solve a problem, and its implementation. The former could be studied without paying attention to the latter.
The developments in information processing and artificial computation provided researchers from numerous fields with new intellectual resources for thinking in a formal and rigorous way about cognitive processes. They provided a new terminology for psychological theorists, enabling them to think in terms such as algorithms, information buffers, flow bottlenecks, and recursion loops.
The growing popularity of computational ideas both contributed to and was driven by a parallel change which was occurring simultaneously in the fields of philosophy and psychology. Practitioners in both fields had begun to realize that methodologies which were defined by their insistence upon limiting themselves only to empirically-accessible sense data (behaviorism in psychology, and positivism and verificationism in philosophy) were too limited to explain all the phenomena we might wish to explain (Hebb, 1949). Black box psychology, which treated the brain as an encapsulated unit whose inner workings were not be used in theorizing, would have to be abandoned. The old metaphor of the brain as a telephone switchboard which connected stimuli directly to response gave way to a more complex metaphor which saw the brain as "a map room where stimuli were sorted out and arranged before ever response occurred" (Bruner, Goodknow, and Austin, 1956, p. vii).
A third talk given at the 1956 MIT symposium on information processing directly emphasized the need for postulating such cognitive pre-processing. The speaker was a young linguist who was in the process of single-handedly re-inventing his field: Noam Chomsky. Chomsky proved that the simple computational principles which had been outlined by Shannon were not sufficient to account for human language, and presented a new way of thinking about language which postulated computational transformations across the morphological units of language (Chomsky, 1957). Language, Chomsky claimed, could not be explained unless the black box of the brain was opened up unless theorists allowed themselves to speak of inferred computational events which required operations which had no obvious external manifestation and which went beyond those defined in logic. Chomsky’s work contributed to the growing acceptance of the idea that understanding the mind’s functionality was going to require the development of new ideas about how information could be represented and manipulated. As well as having implications for the kinds of information processing the brain must be doing, Chomsky’s work underscored the need to consider that some kinds of knowledge might be innately specified, hard-wired into the human nervous system at birth.
In the years following the 1956 MIT conference, interest in the promise of the new computational sciences grew rapidly. In 1960 two psychologists at Harvard University Jerome Bruner and George Miller founded the Center For Cognitive Studies. The center was explicitly devoted to furthering the new ways of thinking about thinking, and played a central role in the early years of cognitive science (Posner & Shulman, 1979; Bruner, 1988; Norman & Levelt, 1988). In 1969, the first influential general textbook devoted to the exposition (and criticism) of the ‘new science’ was released: Ulric Neisser’s Cognitive Psychology.
Three years later Newell and Simon the two researchers who had presented the first computer-generated theorem proof at the 1956 MIT conference published their massive book, Human Problem Solving, in which they described a general computational approach to problem solving. Their approach means-end analysis can be seen as an extension to cognition of the cybernetic principle of feedback. In feedback systems, information about the current state of the system is compared to the desired state of the system, and the current state is nudged in the desired direction. This simple principle is widely used in both machine and natural control systems. The application of the idea to cognition is very simple. It involves the comparison (often on several dimensions) of the current state of a problem to the desired goal state, and the application of an operator which reduces the distance between those states. Newell and Simon’s book demonstrated that this simple approach could be used in an algorithmic fashion to solve a range of problems which had previously been considered to require human intelligence. Although its applications have become increasingly sophisticated and its limitations increasingly apparent, variations of the general approach described by Newell and Simon are still widely used in artificial intelligence and cognitive science today.2
Cognitive science received a boost in the mid 1970s, when the privately-administered Sloan Foundation chose to give major funding to cognitive science initiatives. Soon thereafter the discipline’s first dedicated journal, Cognitive Science, began publishing. The new approach to the mind was coming into its own.
In the twenty years since cognitive science became sufficiently well-defined to have its first journal, the discipline has undergone a number of changes. Four in particular have drastically altered (or are currently altering) the field’s basic conceptions about cognitive processing:
i.) the rise of distributed models of mind, and the resulting decline of top-down methods and architectures;
ii.) the integration of neuroscience with cognitive science;
iii.) the emergence of evolutionary psychology; and
iv.) a re-consideration of the role of context in cognitive function.
In this subsection each of these four changes will be briefly considered.
Distributed and bottom-up models of mind are models which build from simple components connected in a network, rather than being based on hierarchically organized top-down architectures. Such models have a long history.
Some influential precursors to today’s models were connectionist models, whose defining characteristics pre-date cognitive science. In 1943, two researchers from MIT who were involved in the development of cybernetics Warren McCulloch and Walter Pitts published a paper in which they proved that simple networks of simulated neurons were sufficient to simulate a Turing machine, and therefore sufficient to compute any computable function. In doing so they founded the discipline that came to be known as connectionism: the study of the information processing capabilities of a network of connected nodes with simple response functions. Six years after McCulloch and Pitts published their paper, McGill University psychologist Donald Hebb (1949) suggested a simple means by which networks of real neurons might come to represent information: "When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased" (p. 62). This idea laid the conceptual foundation for connectionism.
It was recognized early on that computers offered a way of modeling and exploring the properties of neural networks. Pioneering work in connectionism, using an extended version of Hebb’s rule for learning, was done by Rosenblatt (1961), who dubbed the two-layer networks which he studied ‘Perceptrons’, because they were able to learn to ‘perceive’ categories in an input string. A few years later Minsky and Papert (1969) proved that Perceptron networks had serious limitations which guaranteed that they were unable to learn to classify certain kinds of simple input and which would present serious problems of scaling. The criticisms they brought to bear were very specific, applying to a particular configuration of connectionist networks with a particular kind of processing unit. Nevertheless, Minsky and Papert’s book sharply decreased interest in connectionism. Most cognitively-oriented computational work in the decade following the publication of Minsky and Papert’s paper was based on symbolic processing, in the spirit of Newell and Simon’s program. A few researchers (see Churchland and Sjenowski, 1992, p. 78 for details) continued to develop the ideas of connectionism, but little attention was focussed on their work by cognitive scientists.
In the 1980s interest in connectionism exploded. One may only speculate about the reasons behind the sudden revival of interest in this old idea.
Disillusionment with the classical symbol processing program in artificial intelligence was probably one major factor which contributed to the rise of connectionism. Despite huge levels of funding in the United States and Japan, progress in artificial intelligence had been depressingly slow, limited almost entirely to ‘microworld’ simulations which usually did not allow for any generalization to cognitive domains other than the one being simulated. Although Newell and Simon’s general problem solving approach had turned out to be useful for solving a variety of simple puzzles, attempts to apply the approach to real-world problems, where the structure and boundaries of the problem were not necessarily clear, had been quite unsuccessful.
Another likely contributing factor to the renewed interest in connectionism was a growing interest in specifically human cognition as opposed to the strong AI interest in general cognition and intelligence. There was a growing awareness that the computational models being proposed as models of human cognition were, as one commentator writing at the time noted, "ludicrously undetermined" by the data (Dennett, 1984). There was no way to decide if one computational model was a better model of human cognition than another, since any number of widely-variant models could model the data.
The rapidly decreasing cost of and increasingly easy access to computer resources probably played an important role in the rise of connectionism as well. By the mid-1980s, personal computers became fast enough, for the first time, to simulate simple neural networks. By 1986, anyone with access to a personal computer could purchase a software package (McLelland, & Rumelhart, 1986) to build and run a wide range of connectionist model simulations. Many did purchase the package: according to Amy Brand, senior editor at MIT Press, in the first five years of its release, about 40,000 packages were sold (personal communication). This is an enormous number of sales for a specialized academic publication.
A few years later, another reason for the growing popularity of the approach emerged, when connectionist networks began to be used for the first time to shed light upon real neurological phenomena such as dyslexia (i.e. Hinton & Shallice, 1991). This development brought connectionism to the attention of clinicians and researchers who had previously ignored it, since such work enabled connectionist work to be published for the first time in journals that did not specialize in computer modeling.
Although most existent connectionist models of high-level cognition are now widely recognized to be over-simplistic and biologically-implausible, the underlying principle that "intelligence emerges from the interactions of large numbers of simple processing units" (Rumelhart et al., 1986, p. ix) remains an important feature of modern cognitive science. There are now many different approaches to the construction of distributed and bottom-up models of cognition (for an accessible review, see Franklin, 1995). Such models have a number of advantages over the top-down approach: they often have a closer relation to the known microstructure and functioning of the brain than symbolist accounts; they allow one to theorize about the otherwise-mysterious connections between data representation, computational function, neurological structure, and behavioral production in a more concrete manner (see O’Brien & Opie, in press); and they offer new explanations for a number of puzzling discontinuities in the development of cognition (see Elman et al., 1996; Thelen & Smith, 1998). For all these reasons, distributed and bottom-up models and theories are playing an increasingly important explanatory role in contemporary cognitive science.
Although many cognitive science researchers remain true to the original program of studying cognition independently of its implementation in a brain, there is a recent trend towards integrating the study of the brain with the study of cognition. This trend is probably due in part to two events which have already been discussed: the increasing recognition of the theoretical and practical limitations of classical top-down approaches to AI, and the rise of bottom-up computational models as an alternative approach for modelling cognition.
The most important reason for the increased significance of neuroscience, however, is simply that massive progress has been made in the last thirty years in the field. This progress may be partially attributed to the invention (largely by Hebb and his colleagues, William Penfield and Brenda Milner at McGill University) of the subdiscipline of neuropsychology (Hebb, 1949; Penfield & Roberts, 1959), which took the study of the relation between brain and behavior out of the clinic and into the laboratory.3 A related reason for the progress of neuroscience is that technological improvements made in the last thirty years have provided neuroscientists with an impressive array of new tools for examining the functional structure of the living nervous system in human beings and other animals. Whereas 40 years ago the human brain was widely considered to be a black box, today a variety of electronic imaging and stimulation technologies enable researchers to examine the dynamic functionality of the living brain across a variety of temporal and spatial resolutions. In the same period, subtle experimental techniques have been developed which allow scientists to make deductions about the mysterious workings of the black box (see Westbury, 1998 for a partial review).
All this has contributed to a growing understanding that the brain may implement some or all of its computations in unexpectedly complex ways, and to a sentiment that cognitive science cannot proceed if it ignores the insights of neuroscience.
c.) The Emergence Of Evolutionary Psychology
One very recent identifiable trend in cognitive science is an increasing insistence on the importance of thinking of human evolution in understanding behavior and cognition (Dennett, 1995; Deacon, 1997; Bogdan, 1997; Hendriks-Jansen, 1996; Elman et al., 1996; Pinker, 1997). Like the other trends which have been considered, this trend is rooted in a number of changes.
One is a growing understanding that human beings are far from optimal in their intelligence, as considered above, a finding that makes much sense when considered from an evolutionary perspective. Evolutionary thinking tells us that if we want to understand how human beings actually think, it will not be sufficient to create idealized models of cognition. We must study human beings in the light of their evolutionary history, for that history alone can explain why we think the way we do.
A related reason for increased interest in evolution among cognitive researchers is a growing concern that the Chomskian and neo-Chomskian attempts to explain complex cognitive functions (especially language) by reference to innateness is not scientifically satisfactory. There has been a growing realization in recent years that postulating innate structures for psychological functions is not explanatory in itself, but simply a description of what remains to be explained. Psychological theorizing which relies on the postulation of innate structures is in that sense a remnant of the black box psychology that cognitive science was developed to over-throw. An evolutionary approach to psychology places constraints on explanations of the possible genesis of apparently innate structures.
The rise of distributed and bottom-up theories probably also contributed to the increased interest in evolutionary psychology. Such theories of human cognition made possible something which seemed impossible under the classical AI account: the consideration of how incremental changes of the type required by evolutionary theory could have given rise to the kind of apparently qualitative differences which seems to separate animal from human cognition (for a largely symbolist account which does attempt to provide a mechanism for incremental change, see Drescher, 1991). Bottom-up theories do away with the need to posit the existence of complex symbolic data structures as the lowest level of cognitive structure. They also underscore how simple changes of the type which might be easily underlaid by small changes in the genotype can lead to adaptive changes at the functional level (i.e., see Elman et al., 1996, and Deacon, 1997, on homeobox genes). Together these characteristics make it easier to envision how complex psychological functions might have evolved.
Recent advances in conceptualizing evolution in terms of algorithmic processes (Dennett, 1995; Holland, 1995) have made it clear that the explanatory frameworks of cognitive science and evolution are highly compatible. Evolution is now recognized, not simply as a specialized method for enhancing reproductive fitness in successive generations of biological organisms, but as a much more general process which can be used to search any large space of coded possibilities structured in such a way that evolved solutions which are similar in their value are generally represented in increased numbers in the following generation by codes which are also similar.4 As a result of this reconceptualization of evolution, evolutionary processes are now recognized by many to operate at many levels relevant to cognitive psychology. There is increasing evidence that selective processes underlie the processes which guide neurons in the brain to connect properly (see Edelman, 1987; Changeux, 1983), albeit in a fashion which differs from Darwinian natural selection (Van Belle, 1997). Although his idea has not yet achieved the status of being accepted by mainstream cognitive psychology, one theorist has recently proposed that the brain uses true Darwinian natural selection to structure and manage the electrochemical activity which underlies cognition and behavior (Calvin, 1996). An increasing number of theorists have also accepted that evolutionary principles must be invoked at a social level to explain how ideas (or ‘memes’, as the replicable unit of cognition was dubbed by Dawkins, 1976) replicate and survive at a cultural level (Dennett, 1995). In the view of evolution which is starting to emerge, individual organisms are seen as the nexus of multiple evolutionary processes which are taking place at scales both much larger and much smaller than the scale at which classical Darwinian natural selection was believed to operate.
d.) The Role Of Context
In his early history of ‘the cognitive revolution’, Gardner (1985, p. 41) wrote that "Though mainstream cognitive scientists do not necessarily bear any animus against the affective realm, against the context that surrounds any action or thought, or against historical or cultural analyses, in practice they attempt to factor out these elements to the maximum extent possible". Context Tended To Be Treated By Early Cognitive Scientists As Noise, To Be Controlled For But Not Allowed Into Theory5, because "For most psychologists, the idea that context can differentiate cognitive processing is akin to acknowledging the fragility of our theories" (Ceci & Roazzi, 1994, p. 74).
However, empirical data does not respect boundaries which are imposed by human desires. There is now incontrovertible evidence that many functions of interest to psychologists including reasoning (Ceci & Roazzi, 1994; Ferrari & Sternberg, 1998), memory (Anderson, 1982; Chase and Simon, 1973; Ceci & Leichtman, 1992) and even low-level motor control (Mowrey & MacKay, 1990; Kelso, 1995) are more sensitive to context than many early cognitive scientists had hoped. Today an increasing number of cognitive scientists have accepted that accounting for the effects of context is important, or even crucial, to understanding human cognition.
Not all cognitive scientists had ever believed otherwise. Jerome Bruner, who is recognized as one of the founders of cognitive science for his early role in setting up the Harvard Center For Cognitive Study, published a book in 1990 in which he not only approvingly declared that "the contextual revolution (at least in psychology) is occurring today" (p. 105-106), but also insisted that the current growing interest in context constituted a return to one of the original, long-neglected goals of cognitive science. Bruner's vision for psychology, which he calls ‘transactional contextualism’, emphasizes action in context as being constitutive of experienced meaning. Bruner’s vision is receiving increasing support from recent developments in generalizing evolutionary theory to apply it in the cognitive domain, from work which stems from a re-appraisal of the requirements and role of artificial intelligence (and computationalism in general) due to the limited success of classical symbol-processing methods, from a renewed insistence on the importance of ethological studies of animal and human behavior, from the successes of psychology in breaking up apparently unitary behaviors into increasingly fined-grained micro-behaviors, from the rise of neurophilosophy, and from developments in two closely-related and heretofore obscure fields of enquiry: situated robotics and artificial life (for a detailed discussion of these links, see Hendriks-Jansen, 1996).
Most commentators (i.e. Ceci and Roazza, 1994; Ferrari & Sternberg, 1998) identify three contexts which need to be taken into account in understanding human cognition: the biological context, the environmental context (including the social context), and the mental or epistemological or symbolic context (or domain).
The biological context
The biological context consists of the limitations and abilities that are built in to the subject’s nervous system: both their innate predispositions (shaped by genetic specification and the pre-natal environment) and learned behavior which has been shaped by the external environment after birth. There are many examples of the latter, but perhaps the most salient is the child’s phonemic distinction. It has been clearly established that children are capable of differentiating a much larger range of linguistic sounds when they are first born than they are able to differentiate some years later, after having been exposed to the phonemes used in the language or languages spoken in their environment (Remez, 1987). Their brain adapts to the environment in which it finds itself.
Our brains have been adapted by natural selection to solve certain kinds of problems faced by our evolutionary ancestors: problems dealing with hunting, gathering, escaping from predators, mating, and child-rearing. There has not been sufficient time for our brains to evolve in any appreciable manner since the time when such problems were our sole concern: we can be sure that we have the same brain as our hunting and gathering ancestors. Since the problems that brain was adapted to solve are highly limited in many dimensions, we must expect that the human brain will be limited in its ability to deal with other dimensions of experience. Selection for an ability to solve the kinds of problems faced in our evolutionary past immediate problems involving medium-sized solid objects which behave in an easily predictable manner would undoubtedly leave certain ‘functional holes’ in our cognitive architecture, for the simple reason that there was no selective pressure to plug those holes during our evolutionary history. Cognitive researchers have in fact identified a number of universal, systematic cognitive biases, especially in probabilistic and formal reasoning (see Kahnemann, Slovic, & Tversky, 1982; Piatelli-Palmarini, 1994). Human beings are extremely poor even after extensive training at combining probabilities or computing functions which require them to hold large amounts of information in mind6.
The human nervous system also has some innate strengths. For example, it is exceptionally good at parsing visual information, especially when that information is coded by color and/or motion. Cognitive scientists have identified a number of domain-specific innate cognitive strengths. Much evidence from very young infants suggests that we are born with or are very rapidly able to acquire limited and rough knowledge (‘folk knowledge’) of some aspects of many domains, including physics, biology, and psychology (see Wellman & Gelman, 1998). Although the innate knowledge is not always consistent with modern scientific understanding of that domain, it provides a rough guide to how the world works, and constrains later conceptual undertstanding on those areas. To consider just a single example, evidence from studies using a behavioral measure of violated expectation suggests that infants already understand by the time they are four months old that mattter does not pass through solid objects (Spelke, 1988, 1994).
Gardner has been drawing attention for many years to another effect of biological context: the individual differences between people in their innately-specified strengths. He has introduced the idea of ‘Multiple Intelligences’ (or MIs, which are roughly equivalent to what is sometimes called ‘cognitive styles’ by others) to emphasize the fact that people vary in their biologically-specified proclivities. Since people have different strengths that may manifest themselves in different domains, Gardner argues, intelligence should not be viewed as a unitary attribute, but rather as a rich set of independent strengths (Gardner, 1983, 1991, 1993; Ferrari & Sternberg, 1998). The original seven intelligences he outlined were linguistic, logical-mathematical, musical, bodily-kinaesthetic, interpersonal, and intrapersonal, although Gardner does not believe this original list is necessarily complete.
The environmental context
The context in which a human being is living, learning, and working has many effects on the way he views his abilities and skills. In this section, we will consider only the effect of the social environment.
On an evolutionary time scale, the systematically-structured type of thinking which characterizes scientific work is a totally new phenomenon. If we imagine compressing the time since Homo Sapiens first started using language (no more than 350,000 years ago) until today into a single 24 hour day, then the first recorded general problem representation (geometry, invented by Thales of Miletus about 450 B.C.) would have appeared only 9 minutes and 30 seconds ago; the first systematic large-scale collection of empirical facts (Tycho Brahe’s collection of astronomical observations) would have appeared only a minute and a half ago; and the first mathematical equation which was able to predict an empirical phenomena (Newton’s 1697 equation for planetary motion) would have appeared only one minute and twelve seconds ago. These late-appearing ideas were all important in the development of the modern Western scientific tradition. Their remarkably late historical appearance suggests that the ideas are not be ‘natural’ or simple for human beings. It is a significant feat of human civilization to have created these ideas -- ideas that only came to light through They were developed and nurtured only with considerable effort and nurturance.
Much of the understanding and ability that we have in today’s world is made possible only because the world ‘scaffolds’ that knowledge: that is, it provides a framework which presents that knowledge in a comprehensible way. Arguing from a cognitive science perspective, Margolis (1993) has claimed that much of the scaffolding work done by the social environment works by breaking down ‘habits of mind’ which are entrenched, often unconsciously, in the way we act in the world. He claims that "the central puzzle to understanding what binds together a certain community (making communication easy within the community and making it hard to communicate with a rival community when one appears) would be identification of habits of mind which tacitly guide critical intuitions within that community in ways that would not come easily or seem reasonable to someone who is not a member of that community and who therefore lacks the intense experience with seeing things in particular ways that are characteristic of members of that community" (p. 23).
Margolis provides some evidence for his theory by analyzing several historical scientific paradigm shifts, and showing that those first exposed to such shifts often failed utterly to appreciate their correctness, even when the issue was totally formal and easily understood. For example, he shows that the emergence of elementary probability theory in the 1650s met with enormous resistance and lack of comprehension when it was first introduced, despite its formal character, its utility, and (what we now recognize as) its simplicity. The implication is that the general knowledge of a community can impact on understanding in subtle ways.
The mental context
The third context which can affect cognition is the mental or epistemological context. As Margolis’s work emphasized from a social level, what one knows when one tries to learn something new can impact on ones ability to learn the new piece of informationAs was demonstrated early in the history of cognitive science, it is easier to learn new information when it is linked to knowledge that is already known (Chase and Simon, 1973) than it is to learn disconnected facts. This finding has been explained in terms of elaboration: the process of using known facts to embellish new information, so that the learner has multiple access routes to that new information, and is able to build networks of interconnected knowledge instead of being forced to remember isolated meaningless facts.
The importance of these three contexts will be spelled out in more detail in the following sections, since all three of them are important in understanding the impact of cognitive science on education.
Let us return to the original question: What is cognitive science? As a working definition, we may say that cognitive science is a multi-disciplinary approach to studying how mental representations enable an organism to produce adaptive behavior and cognition. Although this definition is extremely general, it captures the three aspects of cognitive science which have always been important in the field: a faith in the necessity of multi-disciplinarity, an agreement that the object to be explained is behavior and cognition, and a recognition that internal knowledge representation is relevant to that explanation. However, the definition leaves open one very important question: what is a mental representation? It is to this question that we must now turn our attention.
Defining representation has been the central problem of cognitive science since it began. As we have seen, cognitive science emerged largely in response to the perceived need for a theory of mental representation. However, despite the fact that the definition of representation lies at the root of cognitive science, no universally-accepted definition of mental representation has yet been suggested. Moreover, it seems increasingly unlikely that any such definition will ever be forthcoming, because mental representations seem increasingly unlikely to be the sort of thing which can be defined as a unitary class. Mental representations are not a single type of thing, but a name we can use to refer to many different types of accessible information storage. Many apparently unitary representations are multiply-constrained at the neurological level: for example, such an apparently basic function as object recognition is subserved by multiple separable neurological pathways. Other mental representations (such as representations of intentional7 states such as beliefs and desires) may be functions of language, existing as a result of the way words are encoded, rather than underlying that encoding as pre-existing entities waiting to be named (Dennett, 1987). Some representations which seem like static data structures are inextricably linked to behavior, and thereby may be more appropriately conceptualized as computational processes rather than static structures (for discussions, see Hendriks-Jansen, 1996; Westbury, 1998).
Numerous other complications make it impossible to give a definition of mental representations which is simultaneously simple, general, useful, and neurologically-plausible. In this section, we will consider a definition of mental representation which has the greatest utility in understanding and talking about education. This is the problem-space representation. The problem-space representation is a general, substrate-neutral framework for thinking about all goal-directed processes. Inasmuch as there is no education without some goal –whether it be to deepen understanding, facilitate the acquisition of skill-mastery or to increase retention of remembered facts –it has found a general application within education.
The classical definition of problem-space representation comes from the problem-solving literature in cognitive science. Early work on formalizing problem-solving recognized that any problem could be decomposed into a number of distinct elements. In order to define the elements clearly, let us consider a trivially simple concrete example: the problem of ordering the elements in the following set into alphabetical order: {b, a, d, c}.
Two important elements of any problem are the initial state and the goal state.
The initial state is the state of the problem when it is first recognized as a problem. In our example, the initial state is the set as it was presented when the problem under consideration was defined: {b, a, d, c}. In education, the initial state is usually conceived of as a state of unrefined knowledge in some specified knowledge domain.
The goal state of the problem is the state which must be arrived at for the problem to be considered solved. Since the problem given as an example is to order the set in alphabetical order, we know that the goal state is {a, b, c, d}. Of course, in many problems encountered in real life, we do not know the goal state itself. For example, in mathematical problems we are not usually given the answer in advance! However, when the goal state is unknown, there must always be some means of recognizing it –some way of knowing when the problem is solved. Without that, the problem is too ill-defined to be soluble: How could we ever solve a problem if we would not know we had solved it even when we had?
In order to change the initial state into the goal state, it is necessary to have a mechanism or a set of mechanisms for changing the initial state. Those mechanisms are called ‘operators’. In our simple example, we will allow ourselves just a single operator, called ‘flip’. The flip operator allows us to change the order of any two consecutive elements in a set. For example, we can flip the first two elements of our initial state {b, a, d, c} to get the set {a, b, d, c}.
After an initial state and a set of operators has been defined, we will have defined an abstract representation of the problem called the ‘problem space’. The problem space is the set of all possible states the problem solver can construct from the initial state using the available operators. The problem space for our example problem consists of all possible permutations of the four elements in the initial set, since the flip operator makes it possible to generate any possible ordering, as illustrated in Figure 1.
It is important to note that there is, in general, nothing prescriptive about a problem-space representation that is, the representation does not tell us how a problem should be solved. A problem state representation simply describes a problem within the constraints of a specified problem state space and the available operators. A single problem may admit of multiple different representations, which differ because the initial state is described differently and/or because a different set of operators is applied to that state. Imagine if, in our example, we had an operator called ‘Alphabetize’, which acted on a set and returned that set in alphabetical order. In that case, our example problem could be solved very simply indeed, by a single application of the ‘Alphabetize’ operator. Because different ways of representing a problem can directly affect how that problem will be solved, choosing an initial state description and a set of operators is a vital step in problem solving. Sometimes we can choose which operators we will apply to a problem, and sometimes they are pre-specified. When the operators are not pre-specified, then choosing a set of operators becomes a problem in itself.
There are two types of methods to adopt in choosing operators, known as weak and strong methods. Weak methods (so-named because they make weak demands on knowledge specific to the task at hand) are general, all-purpose methods which require little or no specific knowledge about the problem. Two weak methods which have been commonly used are hill-climbing, and means-ends analysis, both examples of a more general method called generate-and-test i.e. of generating a possible solution to a problem, and then evaluating that solution.
In applying hill-climbing, a problem solver simply does anything which brings him closer to the goal state. Mean-ends analysis, which was discussed briefly above, is only a little more sophisticated. In applying mean-ends analysis, a problem solver does not simply choose the first available operator which brings the state of the problem closer to the goal state. Instead, the problem solver analyzes the end he would like to achieve. If he has an operator that will help him achieve it, he uses that operator. However, if he has no operators available for achieving or getting closer to that end, he creates a subgoal of finding such means: that is, he sets himself a new problem, which is to find the means he needs to achieve the original goal. Newell and Simon (1972) gave an example in their book, Human Problem Solving:
"I want to take my son to nursery school. What’s the difference between what I have and what I want? One of distance. What changes distance? My automobile. My automobile doesn’t work. What is needed to make it work? A new battery. What has new batteries? An auto repair shop. I want the repair shop to put in a new battery; but the shop doesn’t know I need one. What is the difficulty? One of communication. What allows communication? A telephone..." (p. 416).
Sophisticated variations of these simple general methods underlie many successful AI applications, and are still widely used today.
Strong methods for choosing operators are methods which are not general, but particular to the kind of problem being addressed. For example, in solving the problem of trying to get a broken vending machine to work, we might try kicking it first, not because we believe this is the most likely operator to solve the problem, but simply because it is the easiest operator to apply. However, the operator ‘kick’ is of no utility at all in solving most cognitive problems.
Choosing an initial problem state is as important as choosing appropriate operators. In our example the problem state was specified when the problem was presented. In real life the problem-solver must often choose his own problem representation that is, he must decide which elements of the problem he is going to encode. How he decides to think about the problem will determine how it is solved. There are no domain-general guidelines for choosing a problem representation, which is largely a problem of creativity.
Posner (1973, p. 50) gives a good example to illustrate the importance of choosing an appropriate problem representation. He describes the following classical mathematics problem:
Two trains leave one Saturday afternoon at 2 o’clock from each of two railway stations. The stations are 50 miles apart. As soon as one train starts moving, a bird jumps up from the front of the train, and flies in the same direction as the train, but at a faster speed. As soon as the bird reaches the second train, which is driving in the opposite direction to the first train, it turns around and flies back to the first train. When it meets the first train, it turns around again. It continues to fly back and forth between the two trains until they meet. The trains travel at 25 miles per hour and the bird flies at 40 miles per hour. How far will the bird have flown by the time the two trains meet?
Posner points out that if this problem is represented in terms of distance, it is quite a difficult problem, requiring the summation of a set of decreasing distances whose calculation is a function of the time, the trains’ speed, and the bird’s speed. However, if the problem is represented in terms of time, it becomes trivial. The trains are 50 miles apart and traveling towards each other at a speed of 25 miles per hour each, for a total speed of 50 miles per hour, therefore it takes them one hour to meet. Since the bird flies at 40 miles per hour, the answer to the problem is that the bird flies 40 miles. A simple change in the problem representation can make a difficult problem simple8.
Some researchers have argued that more complex representational spaces than those considered so far are necessary for understanding cognition. For example, Klahr & Dunbar (1988) examined how students approached the problem of designing experiments to deduce the function of a button on a programmable electronic device. They argued that the strategies used by the subjects to solve the problem could best be described in terms of simultaneous, mutually-constraining searches through two spaces: the experiment space, which consists of the set of all possible experiments that might be run (roughly equivalent to the problem space representation considered above), and the hypothesis space, which consists of the set of all possible hypotheses of the solution to the problem (roughly equivalent to an operator space). Klahr & Dunbar proposed that this dual space search provides a general model of scientific reasoning.
Although it is possible to conceive of even more complex representations encompassing additional representational spaces and higher-order spaces, the single problem space representation is the most common representation considered in cognitive science. Note that in most educational settings, the operator space is pre-defined, since students are usually explicitly told what cognitive tools they should be using to solve a problem. In this document we will consider only single-space problem representations.
The problem-space representation is very general, which is both its strength and a weakness. Generality is a strength because it allows for the description of many different problems in the same general framework, emphasizing certain aspects which are common to all problems. However, the generality of the problem-space representation is a weakness when the question of which problem-space a particular problem solver is using is under-determined, as if often is, by that facts. Although some excellent empirical work has been done in discovering the underlying problem-space for some simple problems with limited room for errors (for example, beam-balancing problems and subtraction problems, both of which are considered below), and although such micro-genetic analyeses of learners are becoming more common in more complex domains, it remains difficult to discern the problem-space for problems which are either more complex, or simply less amenable to description within a formal framework.
Because both education and cognitive science are fundamentally concerned with problems of epistemology, cognitive science research is relevant in innumerable ways to the goals of education. In this section we will focus on two main lines of research. In the first subsection I focus on research which is relevant to the achievement of one of the main goals of education, whether it be formally-presented eduation in a school, or education obtained in the normal course of day-to-day living: enabling a learner to successfully apply what he or she has learned. In the second subsection, we will focus on research which is more directly relevant to a failure to achieve that goal: research which sheds light on innate limitations of the human cognitive system.
In the early days of cognitive science, there were high hopes that general principles underlying all intelligent behavior and human expertise would be found i.e. hope that weak methods were all that was needed. However, the limitations of general problem-solving approaches became apparent when it became clear that highly-touted AI programs which relied on weak methods, such as Newell and Simon’s General Problem Solver, were in fact very limited in the range of problems they could solve.
This realization spurred the development of a new subfield in cognitive science: the systematic study of expert human knowledge. It was hoped that a deeper understanding of how human experts stored knowledge might reveal new general principles about how to represent and manipulate knowledge.
Perhaps the best-known and influential early experiment in this area was a study of expert chess players carried out by Chase and Simon (1973). Chase and Simon exposed expert and novice chess players to chess boards taken from actual chess games for 5 to 10 seconds, and then asked their subjects to try to place all of the 25 chess pieces which had been on the board. They found that expert players were able to place 90% of the pieces correctly, while novices could place only 20%. They then showed that the experts’ recall performance dropped to the same level as the novices’ performance if the chess pieces were distributed in a wholly random manner about the board, rather than being taken from real chess games.
This work was latter replicated in a number of other domains: experts’ always showed superior memory performance for recalling items within their domain of expertise, but not for items in general. This series of experiment suggested two conclusions.
The first was a negative conclusion which will be pursued in the next subsection: the conclusion that expertise in one domain relied on strong methods which are limited to that domain, and does not rest on general skills (weak methods) which transfer between domains. Knowledge and expertise are then, to a large degree, domain-specific.
The second conclusion to be drawn from these experiments was that experts do not carve up the problem space in the same way as non-experts. The ability of expert chess players to recall the positions of roughly 22 chess pieces far exceeded the general limitation on short term memory of 7+/-2 units which had been demonstrated by Miller. However, the failure of these experts to generalize their superior recall ability to other domains made clear that their ability was not due to a general increase in memory capacity. The only possible conclusion was that they must be chunking their knowledge in a different way, memorizing the same number of units as the novices, but identifying a much more complex unit than the novices did.
Many experiments have since confirmed and expanded on this conclusion. Chi, Glaser, and Rees (1982) studied expert and novice physicists’ understanding of physics problems by asking them to categorize word problems, classifying similar problems into the same categories. They found that while the novices relied primarily on surface features (such as whether the problem involved springs, inclined planes, or pulleys), the experts put problems together based on the kinds of laws which were required to solve them. Since their categorization relied upon general principles of physics rather than overtly visible characteristics, the experts’ categorization categorized together problems that did not share any surface features.
In a more narrowly-defined domain, Siegler (1985) was able to identify a precise set of rules used by three levels of novices (based on their errors) and experts (based on an analysis of solution times) to solve balance scale problems, which require subjects to decide whether a balance scale with weights on it will tip left, right, or remain balanced. He concluded that experts use bigger chunks of knowledge and more complex rules for combining those knowledge chunks than novices did.
Findings such as these imply that experts are not doing the same thing as novices, just doing it better. Experts are not simply faster computers than novices. Rather, they are a different kind of computer: they use entirely different problem-representations and apply different operators than novices.
Related results come from comparing studies of learners in different environments. The results from such comparisons indicate clearly that different problem representations do not occur only between subjects with differing levels of expertise, but also within in a single subject, due to differences in the context in which the problem is presented (see Ferrari and Sternberg, 1998; Rogoff, 1998; Ceci and Roazzi, 1994; Sternberg & Wagner, 1994)
Lave (1988) provided an in-depth analysis of a series of studies which she conducted to compare the ability of 25 adult subjects to solve mathematical problems in a test situation to their ability to solve formally identical problems in real life situations such as shopping and dieting. Lave showed that there were discontinuities between the two contexts in overall level of performances, types of errors, and procedures used to solve the problems. Subjects tended to be much more accurate in solving arithmetic problems in the naturalistic and simulated real-life situations (average 98% in naturalistic situations and 93% in a shopping simulation experiment) than they were at solving problems of the same type (average: 70%) in a formal testing situation. In solving real-life problems, strategies included left-to-right calculations (i.e. decomposition of a number into hundreds, tens, and ones, and beginning comparison with the largest numbers), rounding, transformation of problem and solutions in the course of solving (i.e. deciding to take the largest box for reasons unrelated to whether or not it was the better buy), and the use of the environment as a source of information (i.e. direct comparisons of container size as a clue to the correct answer). Most of these strategies could not be used in solving the math problems, so subjects used entirely different strategies. All subjects relied on right-to-left calculation, used borrowing and carrying routines which they did not use in real-life situations, and re-checked divisions using multiplication and successive subtractions.
Brazilian researchers (Carraher et al., 1982, 1983; Carraher and Schliemann, 1982) have reported related findings from their study of poorly-educated fruit-vendors in Brazil. They were able to show that many fruit vendors could solve problems beyond their educational level, and that they did so using strategies which were not the strategies taught in school. For example, they approached a 12-year old coconut vendor with a Grade 3 education, and asked to buy 10 coconuts. The price of one coconut was 35. The vendor calculated the price of ten coconuts in the following manner: "Three will be 105; with three more that will be 210. I need four more. That is....315....350" (Carraher, Carraher, and Schliemann, 1983, p. 8). It is clear that the vendor’s strategy in solving the problem of pricing ten coconuts depended upon his representing the problem as a function of addition across the (calculated or memorized) price of 3 coconuts, as: (3 x 35) + 105 + 105 + 35. This gives the correct answer. However, it finds that answer using an idiosyncratic problem representation which was never formally taught to the vendor. The researchers’ view of the implications of their findings is aptly summarized by the title they gave the paper in which they reported their findings: "Na vida dez, na escola, zero" [In life: 10; In school: 0]. When the demands of real-life situations force people to solve problems, they find ways to solve those problems even if they have not been formally taught how to do so.
Even small differences in the way a problem is presented can induce subjects to use different problem representations in solving the problem, sometimes in ways which are quite systematic across subjects. A good example was given by Johnson-Laird (1983), who showed robust differences in an ability to solve two forms of the same logical puzzle depending on how it was presented. In the first case, subjects were shown four cards, labelled ‘E’, ‘K’, ‘4’ and ‘7’. They were asked to specify which of the four cards needed to be turned over to test the following rule: If a card has a vowel on one side, then it has an even number on the other side. The correct answer is that two cards must be turned over: the one labelled ‘E’ and the one labelled ‘7’. The former must be turned over to make sure that it has an even number on the other side. The latter must be turned over to make sure it doesn’t have a vowel on the other side. Most subjects answer the question incorrectly, either because they specify that only the card labelled with ‘E’ needs to be turned over, or because they suggest that the card marked ‘4’ must also be turned over, ignoring the fact that the rule specifies a contingency in one direction only (i.e. it only specifies that cards with a vowel on one side must have an even number on the other; it does not say that cards with an even number on one side must have a vowel on the other side). Only 12% of subjects studied by Johnson-Laird correctly indicated that the card marked ‘7’ needed to be turned over.
Results of his second experiment were very different. In that experiment, the cards were labelled ‘Manchester’, ‘Sheffield’, ‘Train’ and ‘Car’. Subjects were told that one side of the card showed a destination, and the other showed the means used to get to that destination. They were asked to specify which cards needed to be turned over to test the following rule: Every time a person goes to Manchester, he goes by train. The correct answer is ‘Manchester’ and ‘car’. Most subjects solve this puzzle correctly: 60% correctly understood that they needed to turn over the card marked ‘car’, corresponding to the much-neglected card marked ‘7’ in the first puzzle. The discontinuity in performance is remarkable because the two problems are formally identical, except for the labels, which are irrelevant to the logical structure of the puzzle. Subjects find the second puzzle easier because it deals with a possible real-life situation, showing once again how contextual information can influence cognition. Such context-sensitivity of problem-solving has been advanced as an argument for evolutionary pressure for context-sensitive mechanisms (Cosmides & Tooby, 1995).
Echoing philosophical arguments first made by Wittgenstein (1958) and recently championed by an increasing number of contemporary cognitive theoreticians (Clark, 1997; Hendriks-Jansen, 1996; Maturana and Varela, 1980; Varela, Thompson, & Rosch, 1991; Shore, 1996; Smith, 1996; Cole, 1996), Lave (1988) argues that the results from these and other studies of reasoning in context "challenge theoretical boundaries between activity and its setting, between cognitive, bodily, and social forms of activity, between information and value, [and] between problems and solutions" (p. 3). Problem-solving strategies are not fixed attributes of either individuals or problems: they rather emerge as an interaction between an individual’s knowledge and the context in which that knowledge is to be applied.
The last two subsections have briefly reviewed findings relevant to successful learning that have been uncovered by arduous research. Neither the chess experts considered in the first subsection, nor the normal subjects considered in the second subsection had insight into their own problem-solving strategies –these had to be deduced by the cognitive scientists studying them. If learners could learn to evaluate their own problem representations, it should make it easier for them to assess the efficacy of that representation, and thereby make it possible to alter the representation when it was found wanting. This evaluative ability involves a level of analysis which is of a higher order than the level of the problem space representation (that is, it concerns itself with how to define such a problem space, not how to work within one which has already been defined). Cognitive scientists call the skills which are necessary to conduct an analysis at this level ‘metacognitive skills’.
When they first defined the notion of metacognition, Flavell and Wellman (1977) identified four levels of mental activity. The first level is concerned with implementation details: the hard-wired basic processes that are ‘built-in’ to the brain, by which the representation is actually instantiated in the brain. The second level is concerned with accessing semantic storage: the retrieval of organized sets of facts relevant to the representation. The third level depends upon the second, consisting as it does of methods and strategies –the means by which we choose the operators we will bring to operate on any problem state. The fourth level is what Flavell and Wellman called the metacognitive level. This level consists of all knowledge, awareness, and (conscious or implicit) control of the lower levels of cognition. Examples of metacognitive skills are:
- an awareness of the difference between understanding and memorizing;
- knowledge of which strategies to apply to choose new operators relevant to a current problem;
- an ability to understand what it is that one does not understand;
- an ability to understand when an explanation offered by another is relevant to ones own way of thinking about a problem;
- the ability to monitor ones own progress, for example by checking the plausibility of sub-steps in problem solving in order to be able to recognize early on when one has likely made an error, or to assess ones own level of comprehension;
- the ability to check attained solutions to see if they are plausible and correct.
Much research suggests that variation in metacognitive skills can account for some differences in learning and understanding. Bransford et al (1986) showed that skilled learners used more meta-cognitive strategies than less-skilled learners. In particular, he showed that the less-skilled learners were less likely to be able to assess whether a text is easy or difficult and therefore less likely to appropriately adjust the time they devoted to different texts; that they were less likely to appreciate the difference between memorization and understanding and to use different strategies for each; and that they were less likely to examine themselves in order to test for possible misconceptions. Markman (1985) showed that less skilled readers were less likely to notice contradictions in passages they had just read, which she attributed to differences in the on-going monitoring of comprehension. Brown and her colleagues have had success teaching metacognitive skills to improve performance in a number of domains with a number of different populations. Training in metacognitive skills, for example, has been shown to improve performance in memorizing skills in mentally retarded students (Brown et al., 1979); in text-summarizing skills in college students (Brown et al., 1981), and in analogical reasoning skills in young children (Brown, 1989).
The interest in meta-cognitive skills, which have broad application across a number of knowledge domains, was spurred in part by a distressing early finding of cognitive science that has already been mentioned: the discovery that there is relatively little transfer between knowledge domains. Learning about one thing does not help much in understanding other, similar things. In the last section some early evidence which supported this claim was introduced: the finding by Chase and Simon that superior memory performance of experts as limited to the domain of their expertise. In that section one reason was given why experts might be limited in this way: the fact that even small changes of context can lead the subject to change the problem representation which he or she uses. Decades of experimental findings in many domains (too numerous to review here) have given this claim strong support (see e.g., Anderson, 1983; Bransford et al, 1986; Chase & Simon, 1983; Cheng et al, 1986; Chi et al, 1981; Gick & Holyoak, 1980; Glaser & Chi, 1988; Hayes & Simon, 1977; McCloskey, 1983; Nisbett, 1980; Reed, Ernst & Banerji, 1974; Tversky & Kahneman, 1982).
The problem of the domain-specificity of knowledge is of particular importance to education, for the simple reason that students are not tabula rasa [blank slates]. They do not appear in the classroom with empty minds which are utterly devoid of concepts. Instead, students bring varying types of knowledge and problem representations to the classroom. Some children will have problem representations which are compatible with the way concepts are taught in school, so that they will have no need to transfer the knowledge acquired in school into a new domain. Other children, however, may have problem representations which are not well-matched to the representations which will be used in school. Knowledge given at school does not fit into their prior understanding, but rather requires them to transfer knowledge between domains. Because of the difficulty in doing so, such students are at risk of performing poorly.
Several researchers have studied this problem. Griffin et al (1994) studied the naive knowledge of numbers that young children bring to their earliest formal schooling. They began by using the standard strategy of cognitive science which has been described: they attempted to isolate the operators which the children applied to solve simple addition problems. In so doing, they identified a small subgroup of children who were poor in math and who also used two operators which were very rarely or never seen in their peers. In an attempt to understand why these strategies had been adopted only by this subgroup, they developed a detailed test of number knowledge which showed that a significant number of the children in the subgroup lacked a basic framework in which the number knowledge taught in school could be integrated. For example, these students could not say which of two numbers was bigger, or say whether 2 or 5 was closer to 6. Children who lacked this background knowledge were forced to learn math as a rote activity, because the principles behind it were obscured by their ignorance. Based on their findings and a more detailed analysis of number knowledge among successful students, Griffin was able to develop a highly-specific teaching program, called Rightstart, which provided just the specific knowledge that was missing in the subgroup that was poor at math. In testing in real-life environments, the program was deemed a success: children who were given the program in kindergarten achieved significantly higher scores on several different achievement tests at the end of the first grade than did children who had not been given the program.
Similar work has met with success in more complex learning domains. For example, Hunt and Minstrell (1994) studied the naive knowledge of physics that high school students brought with them to an introductory physics class. They expressed that knowledge in a series of statements which accurately captured their students’ beliefs about physics, irrespective of whether those statements were in fact true. For example, they included the statement ‘Horizontal motion keeps things from falling as rapidly as they would if they were moving straight downwards’. Although it is in fact not generally correct, this statement is true in particular contexts: for example, it is true that horizontal movement keeps airplanes from falling from the sky. Many of the other statements collected by Hunt and Minstrell were true in specific situations, but not generally applicable.
After collecting a set of such statements, Hunt and Minstrell designed a physics class which tried to build its lessons on top of the ‘naive physics’ those statements expressed. The program included a computer program which tried to ‘diagnose’ the state of a student’s knowledge in terms of the collected statements, and to link those statements to the more general laws of accepted physics. A variety of measures suggested that this approach was more successful than a standard approach to teaching physics, which ignored or simply refuted students’ prior conceptions about the topic, without attempting to show the student what is worthwhile and right about those conceptions.
In the previous section we introduced the example of a poorly-educated Brazilian fruit seller who was able to break up the problem of calculating the price of ten coconuts into idiosyncratic subproblems which he could solve. The fruit seller’s idiosyncratic problem-solving approach enabled him to arrive at the correct solution to the problem, despite his limited or absent conceptual understanding of what it means to multiply a number by ten in a decimal system. The Brazilian fruit-seller exhibited a dissociation between skill-mastery of a procedure and understanding of that procedure.
The fact that such a dissociation can occur is of fundamental relevance to educators, for the simple reason that most educational assessment tools measure skill-mastery rather than understanding. In particular, most standardized aptitude and achievement tests give information good statistical information about the level of achievement (i.e. they tell how the student performed) but no causal insight at all (i.e. they don’t tell why the student performed as he did). An over-reliance on standardized measures makes it possible for students to figure out ‘tricks’ for solving the most common sorts of problems faced in a test situation, without ever forcing the student to consider why those tricks work, whether there are contexts in which they won’t work, or whether there might be other methods which were more general, more fundamental, or more widely applicable.
In a series of studies, Brown, Burton, and Van Lehn studied the use of such ‘tricks’ in the domain of subtraction problems. After examining thousands of arithmetic problems done by students, they concluded that multi-digit subtraction was for most students an utterly meaningless procedure, which was conducted using rules which were divorced from any understanding of the number system (Van Lehn, 1983). Gardner (1991) gives a good example of a student with such a dissociation: he described a young student who arrived at different answers for a simple addition problem depending on whether she solved the problem by counting on her fingers or adding on paper, but who nevertheless believed that both answers were correct. The student did not understand that the same numbers must always sum to the same value, regardless of how they are represented notationally. In trying to understand how such ‘deep’ misunderstandings could occur, Brown, Burton, and Van Lehn identified a large number of systematic misunderstandings (‘bugs’) which caused children to make consistent types of errors on subtraction problems. They also identified sets of ‘repair rules’ which the students used when they were stymied in a subtraction problem. The repair rules had nothing at all to do with the conceptual nature of subtraction, but were rather based on the children’s appreciation of how the final answer should look. The researchers concluded that the problem for educators was not that students were unable to follow procedures but rather that "students are remarkably competent procedure followers, but...[they] often follow the wrong procedures" (Brown and Burton, 1978, p. 157; see also Ng and Bereiter, 1991; Nicholls, 1984; Schoenfeld, 1985; and, for a classic analysis of the role of conflicting procedures in education, Holt, 1964).
Most problems can be described using a wide variety of different problem representations, which may differ in their generality and ease of calculation. This makes it extremely difficult for an external observer to identify exactly what problem representation any particular student is using, and therefore makes it extremely difficult for an external observer to help the student ‘debug’ the procedure which is being used. The difficulty of the task may be appreciated by considering that cognitive science researchers may often spend months or years trying to specify the range of strategies used in solving any particular problem. Educators do not have the luxury of spending so much time on this task. They therefore have a problem in understanding why their students do not understand.
One possible solution to this problem, as considered briefly above, is to teach children the meta-cognitive skills they need to assess their own progress, so that they can learn to recognize when they don’t understand, and learn to check and debug their own work.
Another possible solution which was explored by Resnick (1982) is the pedagogical use of multiple representations. Resnick taught children how to perform multi-digit subtraction and addition using a dual-representation system. As children performed addition and subtraction on paper using the usual subtraction operators which are taught in school, they mirrored the procedures using multi-colored blocks using operators which required them to physically move blocks. For example, when they carried a digit from the left, on paper, they had to exchange a ‘tens’ block for ten ‘ones’ blocks and physically add one of those new ‘ones’ blocks to the next column to the right. Resnick’s dual-representation method successfully helped her students debug their own understanding, because mistakes which were easy to make on paper were either more obvious or less likely to be made with the blocks representation.
A closely related solution to the problem of ensuring that students have good representations is to have them apply their knowledge in real-life (or ‘simulated-life’) situations, in which errors have immediately observable consequences. Many cognitive scientists have constructed ‘micro-worlds’ (Papert, 1980; diSessa, 1985; Edwards, 1995; Brandes & Wilensky, 1991), using video and/or computer technology. By demonstrating to learners the consequences of their understanding, such microworlds make it possible for learners to spot and correct their own errors.
Some of the most interesting examples of micro-worlds have been implemented in the modeling language StarLogo (Resnick, 1994; Wilensky, 1995; Wilensky & Resnick, in press), a parallel version of the graphical programming language Logo. StarLogo is of particular interest because it allows for the easy exploration of dynamic systems, which often behave in ways which are extremely unintuitive. By providing a set of tools for quickly implementing and testing ideas about the behavior of such systems, StarLogo teaches its users to distrust their first intuitions about their behavior, and to develop more sophisticated intuitions and thoughtful hypotheses about that behavior.
The teaching of meta-cognitive skills, the use of multiple representations, and use of microworlds provide another desirable aspect of learning at the same time that they help learners to debug their problem representations: they provide the learners with a source of feedback about their progress, enabling them to monitor that progress on an on-going basis. There are now extensive literatures in the subfields of behavioral, clinical, physiological, comparative, educational, and social psychology on the importance of task feedback (for accessible reviews, see Seligman, 1991 and Cziskszentmihalyi, 1991). As the popularity of such ‘useless’ recreational activities as video games and crossword puzzles attests, on-going feedback about performance increases the likelihood that people will maintain interest in and achieve satisfaction with the task they are undertaking. In the absence of feedback, humans (and other mammals) exhibit behavioral and physiological signs of anxiety, show a decrement in their task performance, and may give up on the task altogether.
The findings of cognitive scientists studying learning and problem solving have many specific implications for education. In this section, some of those implications will be explicitly presented.
There is a growing educational trend towards constructivism (see Steffe & Gail, 1995), which is premised on a belief that was first stated by the anti-Cartesian Italian philosopher Giambattista Vico in 1710: ‘Verum ipsum factum’, meaning ‘the truth is as same as the made’. Expanding on that phrase, Vico (1710, p. 46) wrote:
"...human truth is what man puts together and makes in the act of knowing it. Therefore science is the knowledge of the genus or mode by which a thing is made."
This belief that knowledge is constructed rather than discovered, and therefore that what we know is this inextricably linked to how we came to know it, is the defining belief of the constructivist position in all its forms.
Constructivist educators believe that students must be provided with contexts which allow them to actively construct knowledge not only to the greatest extent possible, but also in the most fruitful way i.e. in a way which gives the student the most flexibility and accuracy in applying the knowledge. Merely transmitting ideas to learners through lectures is destined to failure as the intended message may be undermined by prior student conceptions, as has been outlined above. Because students construct their understanding on top of their prior conceptions, it becomes crucial for educators to learn as much as they can about student conceptions so that they can devise strategies which maximize the chance that students will construct more sophisticated conceptions on top of their prior knowledge. Papert (1980; 1991) has elaborated on the constructivist stance in a form he calls "constructionism". Constructionists take the further step of calling for learners to externalize their mental constructions in external constructions such as design artifacts or computer programs. In this fashion, the students get help in "debugging" their concepts through debugging the constructed artifact and educators get access to visible products of student constructions.
This document has made clear that the findings of cognitive science which are relevant to education are closely consistent with a constructivist approach to education. The emphasis on self-generated knowledge representations, on an epistemology rooted in evolutionary adaptation and on incremental enhancement of existing knowledge structures, on the multiplicity of possible forms of knowledge representation, on the influence of context on comprehension, on the importance of situated action in learning, and on the multiple individual differences which make necessary an individualized approach to knowledge are all consistent with the application of constructivist principles in education.
Constructivism is sometimes misinterpreted as implying that all student constructions are equally valuable. As scientists, cognitive researchers would be aghast to think that their findings might be used to buttress such conceptual relativism. At the same time that it has provided evidence that human beings use multiple self-generated representations, cognitive science has been able to prove with mathematical certainty that not all knowledge representations are equal. Some paths through a given knowledge space are demonstrably more efficient than others that lead to the same end state. Some knowledge representations are demonstrably conceptually richer, more general, or more useful than others. In availing themselves of the research findings of cognitive scientists, it is important the educators do not ignore the rigor and careful analysis which made those very findings –and all scientific progress –possible. The finding of multiple individual differences in how human beings represent and use knowledge does not change the fact that some knowledge representations are simply better for some purposes than other knowledge representations are. In encouraging students to explore and construct their own knowledge representations, educators must not fail also to underscore this point, and must not fail to teach students who are exploring a topic what others who have explored the same topic have already learned. Siegler (1985) identifies this as one of the main tasks of education, writing that "much of the task of education in problem solving may be to identify the encoding that we would like people to have on specific problems, and then to devise instructional methods to help them attain it" (p. 185). This emphasis on directing the student towards desirable problem representations has also been heavily emphasized in Schank’s work on goal-directed learning (see Schank, 1994/1995; Schank & Cleary, 1995).
Even educational matter which is factual may be taught as problem encoding. For instance, instead of asking students to memorize historical facts and dates, one might ask them to analyze the actions of an historical figure, or to suggest and analyze alternative historical scenarios to the one which actually occurred. Such an approach engages students into becoming active intentional learners, rather than putting the onus on individual students to find an active and intentional approach to memorization tasks.
However, as we have already seen, there is a danger to teaching only problem representations, since skill-mastery and understanding can dissociate. Merely presenting students with an encoding may give students the kind of narrow notational understanding which enables students to successfully solve specific kinds of problems without actually understanding the concepts underlying the problem-solving strategies they are applying. Let us briefly reconsider two suggestions for avoiding this which have already been presented: the use of multiple representations, and the use of real and simulated world representations.
One of the founders of the field of artificial intelligence, MIT’s Marvin Minsky, once wrote that a person doesn’t really understand something until he or she understands it in more than one way. (Minsky, 1985). When a person understands something in more than one way, that person begins to see the principles which underlie that thing, rather than seeing only the principles which underlie a specific representation of that thing. Presenting a student with multiple representational systems constrains the number of possible ways the student can construct a consistent general representation, by forcing a student to ‘debug’ one system against another. Such presentation increases the likelihood that the students’ own internal problem representation will be a general one which reflects real understanding. A good example was Resnick’s success in teaching young learners about subtraction by having them solve problems using both block and paper representation at the same time. Because the block representation did not allow for the same kind of mistakes as the paper representation, each representation constrained the other, enabling students to develop their own consistent representation which reconciled the two systems.
Schoenfeld (1987) claims that he has had success in teaching students about multiple representations and meta-cognition by showing videotapes of other students trying to solve the kinds of problems his students are learning to solve. In criticizing others (which, as Schoenfeld notes, is far easier than criticizing ones self) students become aware both of the purpose of meta-cognition and of the myriad ways in which a problem can be represented and mis-represented.
One simple method of presenting a student with multiple parallel problem representations is to have learners apply their knowledge in real or simulated environments, rather than forcing them to solve problems only on paper using an abstract notational system. When knowledge is applied in the real world, the world serves as its own representation, thereby constraining the kinds of representations that one can have in parallel with it. Many errors of understanding which may be notationally-invisible can be made extremely salient to a learner when those errors lead to undesirable or surprising consequences. Moreover, applied knowledge tends to break down the artificial barriers between academic disciplines, forcing a student to draw on knowledge from many disparate domains simultaneously. This was recognized long before cognitive science was invented. In an essay written in 1929, the French philosopher Simone Weil noted that "a workman who ceaselessly experiences the law of work can know much more about himself and the world than the mathematician who studies geometry without knowing that it is also physics and the physicist who does not accord their full value to geometrical hypotheses. The worker can get out of the cave, the members of the Academy of Sciences can only move among the shadows" (cited in McLellan, 1990, p. 22; see also Anderson, 1982).
Modern technology makes it possible to design artificial micro-worlds which have many of the advantages of the real world, as well as other advantages. Using video or computer technology, it is possible to expose student to situations to which they could not be exposed in the real world, because real-world exposure would be too expensive, dangerous, slow, or unpredictable –or simply because the relevant situations do not exist in the real world. For examples, students using StarLogo can easily simulate traffic patterns (Wilensky & Resnick, in press) which involve the placement and tracking of hundreds of cars, or can simulate gas patterns (Wilensky, in press) at levels which require them to track the motion of individual molecules, gaining easy access to phenomena that would be extremely difficult or impossible to study ‘in the real world’. Since simulated situations can respond immediately to the students just as the real world does, they can allow them to debug their own problem representations in just the same way as the real world allows.
One advantage of micro-worlds which the real world cannot always offer is that the problem difficulty can automatically adjust to an individual student’s competence, either by providing a free-form set of tools for the student to use at his own pace, or by adjusting the question difficulty or hint level in response to his answers. Moreover, micro-worlds have the dual diametrically-opposed advantages of both being able to prevent students from making serious errors (by monitoring and responding to their actions in real time) and of allowing them to make serious errors which would not be allowable in the real world. As examples of the latter, students learning to drive on a computer simulator may be allowed to drive at dangerously high speeds to learn why that is not a good idea, and students learning to make medical diagnoses on a simulator may be allowed to make treatment errors which would have immediately fatal results for real living patients. In this way, microworlds can both constrain and extend the range of reality in ways which can be pedagogically useful.
One of the most robust findings of cognitive science is the finding that human knowledge and procedural expertise is usually highly domain-specific. Understanding or having a particular skill in one domain is unlikely to lead to understanding or having skill in even a closely related domain, because learners tend to represent their knowledge using highly-specific problem representations.
One way of addressing this limitation of human learners is by having students learn about learning, a process which Bateson (1972) called ‘deutero learning’. As well as structuring lessons in ways which reflect an understanding of the limits and strengths of the human cognitive apparatus, as suggested above, it is advisable to make students aware of the effects of their own cognitive limitations and strengths by providing practically-oriented introductory courses to human cognition (Weinstein and Underwood, 1985; Gaskins, 1994). Resnick (1986, p. 43) has argued that the need to implement such a ‘meta-curriculum’ is the main implication of cognitive science for education, writing that an educational practice informed by cognitive theory "would transform the whole curriculum in fundamental ways. It would treat the development of higher-order skills as the paramount goal of all schooling".
The goal of instruction in higher-order cognition should be to try to turn students into what has variously been termed ‘intentional learners’ (Bereiter and Scardamalia, 1989), ‘self-regulated learners’ (Zimmerman, 1989), ‘autonomous learners’ (Thomas and Rohwer, 1986), or ‘active strategic learners’ (Breuer, 1994). All these terms refer to learners who understand that learning must be a consciously recognized and consciously pursued goal, rather than being an automatic by-product of passively attending and recording a lesson. A human cognition course directed at making students better learners should provide those students with cognitive tools which can be used to design methods of maximizing each student’s own particular abilities, and should "include practice in the specific task-appropriate strategies, direct instruction in the orchestrating, overseeing, and monitoring of these skills, and information concerning the significance of those activities" (Brown, 1985, p. 335)
Cognitive instruction can begin early in the educational process: Gaskins (1994) describes a simplified cognitive program called ‘Learning And Thinking’ which is taught to children as young as 8 years old.
Another way of addressing the limitation of domain-specific problem representations is to encourage students to seek aid from or collaborate with students who excel in different areas. Several pilot projects exist which have tried to foster such a community of learners, by encouraging students to share their individual knowledge and skills in a collaborative manner (i.e Scardamalia, Bereiter, and Lamon’s (1994) Computer Supported Learning Environment; Brown and Campione’s (1994) Reciprocal Teaching, and the environment fostered by the Cognition And Technology Group at Vandervilt University (1994)). Such communities of learning recognize that students may have differing interests and skills, but nevertheless may all make worthwhile individual contributions towards a common educational goal.
As we have seen, cognitive science has placed renewed emphasis on the importance of understanding and accounting for contextual effects on cognition. This too has important implications for education. Summarizing their review of context effects on cognition, Ceci & Roazzi (1994) wrote that:
"Our review of work that spans continents, social classes, and levels of formal education shows that the context in which learning occurs has an enormous influence on cognition, by serving to instantiate specific knowledge structures, by activating context-specific strategies, and by influencing the subject’s interpretation of the task itself. Neither context nor cognition can be understood in isolation; they form an integrated system in which the cognitive skill in question becomes part of the context. To try to assess them separately is akin to trying to assess the beauty of a smile separately from the face it is part of". (p. 98)
In order to understand learning, educators must consider not only the task or concept which is being taught, but also the context in which the teaching occurs. They must, for example, consider at least the following:
- the social situation in which that task or concept is defined;
- the materials used for carrying out the task or defining the concept;
- the cognitive tools (operators) which are being taught;
- operators which are not being taught but which might also lead to partial or perfect solutions for the same task;
- the relevant portion of the prior state of the learner’s knowledge base, especially any goals and hypotheses which are relevant to the task;
- the extent to which new information or skills are related to existing knowledge or to the context in which that information or skill will ultimately be used; and
- the meaningfulness to the student of the material being taught.
An understanding of the influence of context on cognition also suggests that reports of purely experimental work which seems to have a bearing on education need to considered realistically. Findings from the carefully controlled environment of a scientific laboratory may not have a simple application in the class room. Educators must learn to be critical consumers of the literature describing scientific results, prepared to evaluate and modify the way scientific findings are used in the particular circumstances in which they are teaching.
Research suggests that a variety of widely variable factors may affect a student’s performance on a given cognitive task, including their innate abilities, their past learning history, their interests, and the context in which learning takes place. If this is understood, it is unreasonable to rank students along a single dimension as many standardized tests and other measures of academic achievement attempt to do (Gardner, 1991). When the outcome of education is understood as a complex function which is calculated across a large number of parameters whose value varies by individual, it becomes important to determine which specific factors play a determining role in the performance of any particular student tested in any particular domain to know the reasons for a students’ performance, rather the simply measuring that performance (Von Glaserfeld, 1995). The findings of cognitive science counsel against adopting the simplifying assumption that the same general factors can account for the performance of any student in a given domain. It is incumbent on educators and administrators who wish to conduct their academic programs in the light of contemporary science to devise assessment strategies which allow students to demonstrate their strengths and weaknesses in a more fine-grained fashion than is allowed for by many current assessment procedures (see e.g., Stroup & Wilensky, in press).
One way of achieving this goal is to provide rich educational environments, which provide students with an opportunity to experience and measure themselves on as wide a range of approaches to any topic as is possible. A student who fails to demonstrate anyaptitude for mathematics on a paper and pencil test may nevertheless be capable of mastering and demonstrating an ability to use exactly the same concepts in the carpentry workshop, or in playing music. It may be possible to foster such inter-disciplinary recognition of concept mastery by encouraging students to find their own real-life, relevant applications for knowledge they are taught in the class room, or by providing students with multiple possible approaches to a single concept. Both of these allow students to develop problem decompositions which work for them. It may also be possible to recognize (and thus build upon) students’ ‘hidden’ abilities, at least in educational institutions which are not large, by explicitly encouraging inter-disciplinary discussions of each student’s abilities. By this means, a mathematics teacher can be made aware, for example, that a student who seems unable to master ratios in mathematics class has nevertheless demonstrated a practical understanding of ratios in (for example) tuning and playing a stringed-instrument in music class. The math teacher may then cast topics in mathematics in terms that the student is already known to understand.
There are obvious practical teaching difficulties inherent in providing such individualized educational programs for students, since they demand a great deal of effort on the part of educators, who do not often have sufficient spare time at work to take on such a time-consuming additional responsibility.
One way to address these practical difficulties is by placing the onus for individualizing his or her own education on the student, by giving each student a choice of which class to attend. By structuring classes within a single academic discipline around particular interests, students could choose to learn about subjects which interested them, while acquiring equivalent instruction in the single core discipline which informs those classes. For example, multiple mathematics classes could offer the same content, but gear that content differently for those students with an interest in finance or music or biology or sports or computer applications, while multiple literature classes could teach the same basic literary skills while drawing examples from a different selection of literature chosen to appeal to those with a similar variety of interests (see Schank & Cleary, 1995).
A second way to address the practical problems involved in individualizing instruction is to use computer technology, as has already been discussed. A computer program can easily offer students a choice of examples for a given concept, drawn from a variety of domains of interest, while ensuring the every student covers exactly the same set of core concepts, if such identity of content is deemed necessary.
Cognitive science has shown that there are many innate limitations to the human nervous system. Human beings are not perfectly logical computers, but have biases to think in a certain manner. It behooves educators to try to avoid relying on the natural weaknesses of the human nervous system, and to exploit its natural strengths. Research suggests a variety of ways that this can be achieved. To consider just a few examples:
- To avoid human memory limitations: In teaching human beings tasks (including such everyday tasks as dealing appropriately with friends, relatives and acquaintances, or such ‘high level’ tasks as medical diagnosis) which require them to synthesize information from their past experience, human beings must be encouraged to rely on external record-keeping, and to distrust their own memories.
- To take advantage of human visual dominance: Complex information presented to human beings will be most readily attended to if it is presented visually, especially if the presentation uses bright color or movement. Information which is presented in the auditory modality or in text or numerical format is much more likely to be ignored.
- To combat domain-specific misconceptions: Educational programs which can identify and explicitly address prior misconceptions directly are more likely to succeed than programs which simply dismiss the students’ preconception as errors. Teachers need to understand not only the best way of understanding the topic they are teaching, but also the most common ways of misunderstanding it. They should understand that errors may not be based on ignorance or simply on a failure to understand, but on a systematically-structured misunderstanding, or on a recoding of the problem in an inappropriate way. This information should be explicitly taught to educators. Teachers confronting a new class should attempt to understand what relevant systematic misconceptions students may be bringing to their classroom.
- To take advantage of learners’ prior conceptions: Going beyond listing misconceptions, educators who can tease out learners’ prior conceptions can structure new material as an incremental path from a student’s prior conception to a more sophisticated expert-like conception. Instead of presenting new material as if it could be learned "whole cloth", educators can focus on connecting the new material to students’ prior conceptions and experiences. (Wilensky, 1993; 1997). This approach prevents students from being stuck and unable to move towards expert conceptions.
- To take advantage of the benefits of active learning and to avoid memory capacity limitations: Educators can use computational environments which offload low-level memory tasks onto the technology allowing learners to actively focus on higher level tasks (see e.g. Pea, 1985.)
- To avoid the problem of insufficient feedback to the learner and underdetermined student theories: The use of computer-based environments can also lead students to test hypotheses and get immediate feedback on their theories.
- To take advantage of innate abilities (MIs): Since it is not always possible to identify which of the ‘multiple intelligences’ a person may excel at, it is desirable to structure instruction a way that addresses many different approaches. Students should be encouraged to apply the concepts of their class to areas of their own particular interest or abilities.
This list is not exhaustive - it is merely a start towards a program of exploiting natural human abilities in education.
Cognitive science arose in large part in response to a growing recognition in the scientific community that no scientific understanding of cognition would be possible without some understanding of how knowledge could be represented and manipulated internally. Insofar as learning may be reasonably construed as a process of changing ones own mental representations (and their behavioral expression) in a controlled way, it would be surprising indeed and would reflect poorly on the progress of the field if advances in our understanding of mental representations and how they change did not have direct implications for education. In this document we have tried to show exactly what kind of contribution cognitive science can make to education.
Brown and Campione (1994) summed up the three major themes of an educational program informed by the finding of cognitive science, as one which concentrated on "active, strategic learning, with the learner’s understanding and control, following domain-specific trajectories" (p. 231; italics added). To say that learning is active and strategic means that the learner plays a decisive role in his or her own education, consciously choosing to learn and deliberately making use of the techniques of meta-cognition to assess and debug his or her own understanding. The emphasis on understanding and control is a corollary of this. For a learner to be actively involved in learning, he or she must be in control of the process of learning, shaping what is being learned in such a way as to build incrementally and carefully on prior understanding. Finally, the emphasis on domain-specificity is due to a large body of data which has shown that human beings are very poor at transferring knowledge between domains, in part because they are highly sensitive to the epistemological and environmental context in which their knowledge was obtained and is being applied.
It is perhaps fitting to end with the words of one of the speakers at the 1956 MIT conference where cognitive science began, the linguist Noam Chomsky. In a speech he delivered in 1970, years before cognitive science had turned its tools to education, Chomsky speculated on the role of education from a historical and humanistic rather than a scientific perspective. He began by approvingly citing the German philosopher Wilhelm von Humboldt, who in 1792 had written that "The cultivation of the understanding, as of any of man’s other faculties, is generally achieved by his own activities, his own ingenuity, or his own methods for using the discoveries of others" (cited in Chomsky, 1970, p. 398). In commenting on Humboldt’s claim, Chomsky (p. 389) neatly summed up the claims that cognitive scientists would be making almost thirty years later. He declared that "Education...must provide the opportunities for self-fulfillment; it can at best provide a rich and challenging environment for the individual to explore, in his own way. .. [Knowledge must, as Humboldt had written, be] ‘awakened in the mind. One can only provide the thread along which it will develop of itself’".
Anderson, J.R. (1982). The Architecture Of Cognition. Cambridge, MA: Harvard University Press.
Bateson, G. (1972). Steps To An Ecology Of Mind. New York, NY: Ballantine.
Bogdan, R. (1997). Interpreting Minds. Cambridge, MA: MIT Press.
Brandes, A. & Wilensky, U. (1991). Treasureworld: A computer-based environment for the study and exploration of feedback. In Constructionism, I. Harel and S. Papert (Eds). Chapter 10. Norwood N.J.: Ablex Publishing Corporation.
Bransford, J.D., Sherwood, R., Vye, N. & Rieser, J. (1986). Teaching Thinking And Problem solving. American Psychologist, 41(10): 1078-1089
Broadbent, D. (1958). Perception And Communication. London, England: Pergamon Press.
Brown, A., Campione, J., and Barclay, C. (1979). Training self-checking routines for estimating test readiness: generalization from list learning to prose recall. Child Development, 50: 501-512.
Brown, A., Campione, J., and Day, J. (1981). Learning to learn: On training students to to learn from texts. Educational Researcher, 10: 14-21.
Brown, A. & Campione, J. (1994). Guided discovery in a classroom of learners. In McGilly, K. (Ed.). Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 229-272. Cambridge, MA: MIT Press.
Brown, A. (1989). Analogical learning and transfer: What develops? In S. Vosniadou and A. Ortony, eds., Similarity And Analogical Reasoning. Cambridge, England: Cambridge University Press.
Breuer, J.T. (1993). Schools For Thought: A Science Of Learning in the Classroom. Cambridge, MA: MIT Press.
Breuer, J.T. (1994a). Classroom Problems, School Culture, and Cognitive Research. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 273-90. Cambridge, MA: MIT Press.
Brown, A.L., Campione, J.C. and Barclay, C.R. (1979). Training self-checking routines for estimating test readiness: Generalization from list learning to prose recall. Child Development, 50: 501-512.
Brown, A.L., Campione, J.C. and Day, J.D. (1981). Learning to learn: On training students to learn from texts. Educational Researcher, 10: 14-21.
Brown, A.L. (1989). Analogical learning and transfer: What develops? In S. Vosniadou and A. Ortony (Eds.). Similarity and Analogical Reasoning. Cambridge, England: Cambridge University Press.
Brown, A.L. & Campione, J.C. (1994). Guided discovery in a community of learners. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 229-272. Cambridge, MA: MIT Press.
Brown, J.S. & Burton, R.R. (1978). Diagnostic models for procedural bugs in basic mathematical skills. Cognitive Science, 2: 155-192.
Bruner, J.S., Goodknow, J., & Austin, G. (1956). A Study Of Thinking. New York, NY: John Wiley.
Bruner, J. (1988). Founding the Center For Cognitive Studies. In W. Hirst, Ed. The Making Of Cognitive Science. Pp. 90-99. Cambridge, England: Cambridge University Press.
Bruner, J. (1990). Acts Of Meaning. Cambridge, MA: Harvard University Press.
Calvin, W.H. (1996). The Cerebral Code. Cambridge, MA: MIT Press.
Carraher, T., Carraher, D. & Schlieman, A. (1982). Na vida des, na escola, zero: Os contextos culturais da aprendigazem da matimatica. Caderna la Pesquisa, 42: 79-86.
Carraher, T., Carraher, D. & Schlieman, A. (1983). Mathematics in the streets and schools. Unpublished manuscript on file at Recife, Brazil: Universidade Federal de Pernambuco.
Carraher, T., & Schliemann, A. (1982). Computation routines prescribed by schools: Help or hindrance? Paper presented at NATO conference on the acquisition of symbolic skills. Keele, England.
Ceci, S.J. & Leichtman, M. (1992). Memory, cognition, and learning. In S. Segalowitz & I. Rapin (Eds.), Handbook Of Neuropsychology. p. 223-240. Amsterdam, Holland: Elsevier.
Ceci, S.J. & Roazzi, A. (1994). The effects of context on cognition: Postcards from Brazil. In: R.J. Sternberg & R.K. Wagner, eds. Mind In Context: Interactionist Perspectives on Human Intelligence. Pp. 74-101. New York, NY: Cambridge University Press.
Changeux, J-P. (1983) Concluding remarks: On the singularity of nerve cells and its ontogenesis. Progress In Brain Research, 58: 465-478.
Chase, W. G., & Simon, H. (1973). Perception in chess. Cognitive Psychology, 1: 33-81.
Chi, M, Glaser, R., and Ress, E. (1982). Expertise In problem Solving. In R. Sternberg, Ed., Advances in the Psychology of Human Intelligence, Volume 1. Hillsdale, NJ: Erlbaum.
Chomsky, N. (1957). Syntactic Structures. The Hague, Holland: Mouton.
Chomsky, N. (1970). Language And Freedom. In: N. Chomsky. For Reasons Of State. Pp. 387-408. New York, NY: Vintage Books.
Churchland, P.S. & Sjenowski, T. J. (1992). The Computational Brain. Cambridge, MA: MIT Press.
Clark, A. (1997). Being There: Putting Brain, Body, And World Back Together Again. Cambridge, MA: MIT Press.
Cognition And Technology Group at Vandervilt University (1994). From visual word problems to learning communities: Changing conceptions of cognitive research. In McGilly, K., Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 157-200. Cambridge, MA: MIT Press.
Cole, M. (1996). Cultural Psychology: A Once & Future Discipline. Cambridge, MA: Harvard University Press
Cosmides, L. & Tooby, J. (1995). Are Humans good Intuitive Statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition, 58(1):1-73.
Cytowic, R. (1989) Synesthesia: A Union Of The Senses. New York, NY: Springer-Verlag.
Cziskszentmihalyi, M. (1991). Flow: The Psychology Of Optimal Experience. New York, NY: Harper Collins.
Dawkins, R. (1976). The Selfish Gene. New York, NY: Oxford University Press.
Deacon, T. (1997). The Symbolic Species: The Co-Evolution Of Language And The Brain. New York, NY: W.W. Norton & Company.
Dennett, D. (1987). The Intentional Stance. Cambridge, MA: MIT Press.
Dennett, D. (1986) The Logical Geography of Computational Approaches: A View From The East Pole. In Brand, M. & Harnish, M. (eds.) The Representation Of Knowledge And Belief, p. 55-79. Tucson, AZ: University Of Arizona Press.
Dennett, D.C. (1995). Darwin’s Dangerous Idea: Evolution And The Meanings Of Life. New York, NY: Simon & Schuster.
diSessa, A. (1986). Artificial worlds and real experience. Instructional Science, 207-227.
Drescher, G.L. (1991). Made-up Minds. Cambridge, MA: MIT Press.
Edelman, G. (1987). Neural Darwinism: The Theory Of Neuronal Group Selection. New York, NY: Basic Books.
Edwards, L. (1995), Microworlds as Representations, Noss, R., Hoyles, C., diSessa A. and Edwards, L. (Eds.), Proceedings of the NATO Advanced Technology Workshop on Computer Based Exploratory Learning Environments, Asilomar, CA, p. 127-154.
Elman, J.L., Bates, E.A., Johnson, M.H., Karmiloff-Smith, A., Parisi, D., Plunkett, K. (1996). Rethinking Innateness: A Connectionist Perspective On Development. Cambridge, MA: MIT Press.
Ferrari, M. & Sternberg, R.J. (1998) The development of mental abilities and styles. In: Kuhn, D. & Siegler, R. (Volume eds.), The Handbook Of Child Psychology, 5th Edition, Volume 2: Cognition, Perception, and Language. P. 899- 946. New York, NY: John Wiley And Sons.
Flavell. J. H. & Wellman, H.M. (1977). Metamemory. In R.V. Kail, Jr. & J.W. Hagen, eds. Perspectives On The Development Of Memory And Cognition, 3-33. Hillsdale, NJ: Erlbaum.
Franklin, S. (1995). Artificial Minds. Cambridge, MA: MIT Press.
Gardner, H. (1983). Frames Of Mind: The Theory Of Multiple Intelligences. New York, NY: Basic Books.
Gardner, H. (1985). The Mind’s New Science: A History Of The Cognitive Revolution. New York, NY: Basic Books.
Gardner, H. (1991). The Unschooled Mind: How Children Think And How Schools Should Teach. New York, NY: Basic Books.
Gardner, H. (1993). Multiple Intelligences: The Theory In Practice. New York, NY: Basic Books.
Garfinkel, H. (1967). Studies In Ethnomethodology. New York, NY: Prentice-Hall, Inc.
Gaskins, I.W. (1994). Classroom applications of cognitive science: Teaching poor readers how to learn, think, and problem solve. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 129-154. Cambridge, MA: MIT Press.
Geertz, C. (1973). Interpretation Of Cultures. New York, NY: Basic Books.
Griffin, S., Case, R. & Siegler, R. (1994). Rightstart: Providing the central conceptuial prerequisites for first formal learning of arithmetic to students art risk for school failure. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 51-74. Cambridge, MA: MIT Press.
Hebb, D. O. (1949). Organization Of Behavior. New York, NY: John Wiley.
Hendriks-Jansen, H. (1996). Catching Ourselves In The Act: Situated Activity, Interactive Emergence, Evolution, and Human Thought. Cambridge, MA.: MIT Press.
Hinton, G.E. & Shallice, T. (1991). Lesioning an attractor network: Investigations of acquired dyslexia. Psychological Review, 98:74-95.
Hogan, J.P. (1997). Mind Matters: Exploring The World Of Artificial Intelligence. New York, NY: The Ballantine Publishing Group.
Holland, J. (1995). Hidden order: How Adaptation Builds Complexity. Reading, MA: Addison-Wesley.
Holt, J. (1964). How Children Fail. New York, NY: Pitman.
Hunt, E. & Minstrell, J. (1994). A cognitive approach to teaching physics. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 51-74. Cambridge, MA: MIT Press.
Johnson-Laird, P. N. (1983). Mental Models: Towards A Cognitive Science Of Language, Inference, and Consciousness. Cambridge, MA: Harvard University Press.
Kahnemann, D., Slovic, P., & Tversky, A., eds. (1982). Judgment Under Uncertainty: Heuristics And Biases. Cambridge, MA: Harvard University Press.
Keil, F.. (1998) Cognitive Science and the Origins of Thought and Knowledge. In: Damon, W. & Lerner, R. (Volume eds.), The Handbook Of Child Psychology, 5th Edition, Volume 1: Theoeretical Models Of Human Development. p. 341-413. New York, NY: John Wiley And Sons.
Kelso, J.A. (1995). Dynamic Patterns: The Self-organization of Brain and Behavior. Cambridge, MA: MIT Press.
Klahr, D. & Dunbar, K. (1988). Dual Space Search During Scientific Reasoning. Cognitive Science, 12(1): 1-48
Koza, J. R. (1994). Genetic Programming II: Automatic Discovery Of Reuseable Programs,. Cambridge, MA: MIT Press.
Koza, J.R. (1992) Genetic Programming: On The Programming Of Computers By The Means Of Natural Selection. Cambridge, MA: MIT Press.
Lave, J. (1988). Cognition In Practice: Mind, mathematics and culture in everyday life. Cambridge, England: Cambridge University Press.
Margolis, H. (1993) Paradigms and Barriers: How Habits Of Mind Govern Scientific Beliefs. Chicago, Ill: University Of Chicago Press.
Markman, E.M. (1985). Comprehension monitoring: Developmental and educational issues. In S.F. Chipman, J.W. Segal, and R. Glaser, eds., Thinking And Learning Skills, volume 2: Research and Open Questions. New York, NY: Erlbaum.
Maturana, H.R. & Varela, F.J. (1980). Autopoesis And Cognition: The Realization Of The Living. Dordrecht, Holland: D. Reidel Publishing Company.
McCulloch, W. & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous system activity. Bulletin of mathematical biophysics, 5: 115-133.
McGilly, K. (1994). Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. Cambridge, MA: MIT Press.
McLellan, D. (1990). Utopian Pessimist: The Life and Thought Of Simone Weil. New York, NY: Poseidon Press.
Miller, G. (1956). The Magical Number Seven, Plus Or Minus Two: Some Limits On Our Capacity For Processing Information. Psychological Review, 63: 81-97.
Miller, G. (1979). A Very Personal History. Talk to Cognitive Science Workshop, MIT, Cambridge,, MA, June 1, 1979. Cited in: Gardner, H. (1985). The Mind’s New Science: A History Of The Cognitive Revolution. New York, NY: Basic Books.
Minsky, M. & Papert, S. (1969). Perceptrons. Cambridge, MA: MIT Press.
Minsky, M. (1985). The Society Of Mind. New York, NY: Simon And Schuster.
Mowrey, R.A. & MacKay, I.R.A. (1990). Phonological primitives: electromyographic speech error evidence. Journal Of The Acoustic Society Of America, 88: 1299-1312.
Neisser, U. (1969). Cognitive Psychology. New York, NY: Appleton-Century-Crofts.
Newell A. & Simon, H. (1972). Human Problem Solving. Englewood Cliffs, NJ: Prentice-Hall.
Ng, E. & Bereiter, C. (1991). Three levels of goal orientation in learning. Journal Of The Learning Sciences, 1(3-4): 243-371.
Nicholls, J.G. (1984). Achievement motivation: Conception of ability, subjective experience, task choice, and performance. Psychological Review, 91: 328-346.
Norman, D.A. & Levelt, W.J. (1988). Life at the Center. In W. Hirst, Ed. The Making Of Cognitive Science. Pp. 100-110. Cambridge, England: Cambridge University Press.
O’Brien, G. & Opie, J. (In press). A connectionist theory of phenomenal experience. To appear in: Behavioral And Brain Sciences.
Papert, S. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York: Basic Books.
Papert, S. (1991). Situating Constructionism. In I. Harel & S. Papert (Eds.) Constructionism. Norwood, NJ. Ablex Publishing Corp. (Chapter 1). p. 1 - 12.
Pea, R. (1985). Beyond amplification: Using the computer to reorganize mental functioning. Educational Psychologist, 20(4): 167-182
Penfield, W. & Roberts, L. (1959). Speech And Brain Mechanisms. Princeton, NJ: Princeton University Press.
Piatelli-Palmarini, M. (1994). Inevitable Illusions: How Mistakes of Reason Rule Our Minds. New York, NY: John Wiley And Sons.
Pinker, S. (1997). How The Mind Works. New York, NY: WW Norton And Co.
Posner, M. (1973). Cognition: An Introduction. New York, NY: Scott Foresman.
Posner, M. & Shulman, G.L. (1979). Cognitive Science. In E. Hearst, ed., The First Century Of Experimental Psychology. Hillsdale, NJ: Lawrence Erlbaum.
Resnick, L.B. (1982). Syntax and semantics in learning to subtract. In T.P. Carpenter, J.M. Moser, & T.A. Romberg, eds. Addition And Subtraction: A Cognitive Perspective. New York, NY: Erlbaum.
Remez, R.E. (1987). Neural models of speech perception: A case history. In S. Harnad, ed. Categorical Perception: The Groundwork Of Cognition. P. 199-225. Cambridge, England: Cambridge University Press.
Resnick, M. (1994). Turtles, Termites, and Traffic Jams: Explorations in Massively Parallel Worlds. Cambridge, MA: MIT Press.
Rogoff, B. (1998) Cognition as a collaborative process. In: Kuhn, D. & Siegler, R. (Volume eds.), The Handbook Of Child Psychology, 5th Edition, Volume 2: Cognition, Perception, and Language. p. 679-744. New York, NY: John Wiley And Sons.
Rosenblatt (1961) Principles of neurodynamics: Perceptrons and the Theory Of Brain Mechanisms. Washington, D.C.: Spartan Books.
Rumelhart, D.E., & McLelland, J., eds. (1986). Parallel Distributed Processing: Explorations In The Microstructure of Cognition, Vol. 1. Cambridge, MA: MIT Press.
Scardamalia, M., Bereiter, C., and Lamon, M. (1994). The CSILE Project: Trying to bring the classroom into World 3. In McGilly, K. Classroom Lessons: Integrating Cognitive Theory And Classroom Practice. p. 201-228. Cambridge, MA: MIT Press.
Schank, R. (1993/1994). Goal-based scenarios: A radical look at education. The Journal of the Learning Sciences, 3(4): 429-453.
Schank, R. & Cleary, C. (1995) Engines For Education. Hillsdale, NJ: Lawrence Erlbaum Associates
Schoenfeld, A.H. (1985). Mathematical Problem Solving. Orlando, FL: Academic Press.
Schoenfeld, A.H. (1987). What’s all the fuss about meta-cognition? In: Schoenfeld, A. Cognitive Science And Mathematics Education. Pp. 189-214. Hillsdale, NJ: Lawrence Erlbaum Associates
Seligman, M.E. Learned Optimism. New York, NY: A.A. Knopf.
Shannon, C.E. (1938). A symbolic analysis of relay and switching circuits. Transactions of the American Institute of Electrical Engineers, 57: 1-11.
Shore, B. (1996). Culture In Mind: Cognition, Culture, And The Problem Of Meaning. New York, NY: Oxford University Press.
Siegler, R.S. & Klahr, D. (1982). When do children learn? The relationship between existing knowledge and the acquisition of new knowledge. In R. Glaser, ed. Advances in Instructional Psychology, volume 2. New York, NY: Erlbaum.
Siegler, R.S. (1985). Encoding and the development of problem solving. In S.F. Chipman, J.W. Segal, and R. Glaser, eds. Thinking And Learning Skills, Volume 2: Research And Open Questions. New York, NY: Erlbaum.
Simon, H.A. (1969). Sciences Of The Artificial. Cambridge, MA: MIT Press.
Smith, B.C. (1996) On The Origin Of Objects. Cambridge, MA.: MIT Press
Spelke, E.S. (1988). Where perceiving ends and thinking begins: The apprehension of objects in infancy. In A. Yonas (Ed.), Perceptual Development in Infancy (Vol. 20, pp. 197-234). Hillsdale, NJ: Erlbaum.
Spelke, E.S. (1994). Initial Knowledge: Six Suggestions. Cognition, 50(1-3), 431-445.
Sperber, D. (1982). Anthropology and psychology: Towards an epidemiology of representations. Man, 20: 73-89.
Steffe, L.P. & Gail, J., eds. (1995). Constructivism In Education. Hillsdale, NJ: Lawrence Erlbaum.
Sternberg, R.J. & R.K. Wagner, eds. (1994). Mind In Context: Interactionist Perspectives on Human Intelligence. Cambridge, England: Cambridge University Press.
Stroup, W. & Wilensky, U. (in press). Assessing Learning as Emergent Phenomena: Moving Constructivist Statistics Beyond the Bell-Curve. In Kelly, A.E. & Lesh, R. (Ed.) Research Methods In Mathematics and Science Education. Englewood Cliffs, NJ: Erlbaum.
Thelen, E. & Smith, L.B. (1998). Dynamic Systems Theories. In: R. Lerner (Ed.),The Handbook Of Child Psychology, 5th Edition, Volume 1: Theoretical Models Of Human Development. p. 563-634. New York, NY: John Wiley & Sons.
Turing, A.M. (1936). On computable numbers, with an application to the Entscheidungs-Problem. Proceedings of the London Mathematical Society, Series 2, 42: 230-65.
Van Belle, Terry (1997). Is neural Darwinism Darwinism? Artificial Life, 3: 41-49.
Van Lehn, K. (1983). On the representation of procedures in repair theory. In H. Ginsburg, ed., The Development Of Mathematical Thinking. New York, NY: Academic Press.
Varela, F., Thompson, E. & Rosch, E. (1991). The Embodied Mind. Cambridge, MA: MIT Press.
Vico, G. (1710/1988). On The Most Ancient Wisdom Of The Italians (L. M. Palmer, Trans.). Ithaca, NY: Cornell University Press.
Von Glaserfeld, E. (1995). A constructivist approach to teaching. In: Steffe, L.P. & Gail, J., eds., Constructivism In Education. p. 3-15. Hillsdale, NJ: Lawrence Erlbaum.
Von Neumann, J. (1958). The Computer And The Brain. New Haven, Co.: Yale University Press.
Weiner. N. (1948) Cybernetics: or Control And Communication in the Animal and The Machine. New York, NY: Wiley.
Weinstein, C.E. & Underwood, V.L. (1985). Learning strategies: The how of learning. In J.W. Segal, S.F. Chipman, and R. Glaser (Eds.). Thinking and learning skills. Vol. 1: Relating instruction to research, pp. 241-258. Hillsdale, NJ: Erlbaum.
Wellman, H.M. & Gelman, S.A. Knowledge Acquisition In Foundational Domains. In: Kuhn, D. & Siegler, R. (Volume eds.), The Handbook Of Child Psychology, 5th Edition, Volume 2: Cognition, Perception, and Language. p. 523-573. New York, NY: John Wiley And Sons.
Westbury, C. (1998). Research strategies: psychological and psycholinguistic methods in neurolinguistics. In: Stemmer, B. & Whitaker, H. (eds.), Handbook Of Neurolinguistics. p. 83-94. New York, NY: Academic Press.
Westbury, C. (Under review). The word as deed: The cerebellum and the ontology of language.
Wilensky, U. & Resnick, M. (in press). Thinking in Levels: A Dynamic Systems Perspective to Making Sense of the World. Journal of Science Education and Technology. Vol. 8 No. 1.
Wilensky, U. (in press). GasLab—an Extensible Modeling Toolkit for Exploring Micro- and Macro- Views of Gases. In Roberts, N. , Feurzeig, W. & Hunter, B. (Eds.) Computer Modeling and Simulation in Science Education. Berlin: Springer Verlag.
Wilensky, U. (1997). What is Normal Anyway? Therapy for Epistemological Anxiety. Educational Studies in Mathematics. Special Issue on Computational Environments in Mathematics Education. Noss R. (Ed.) 33(2): 171-202
Wilensky, U. (1995). Paradox, Programming and Learning Probability, Journal of Mathematical Behavior, 14(2): 251-280.
Wilensky, U. (1993). Connected Mathematics: Building Concrete Relationships with Mathematical Knowledge. Doctoral dissertation. Cambridge, MA: MIT.
Winch, P. (1958). The Idea Of A Social Science. London, England: Routledge.
Wittgenstein, L. (1958). Philosophical Investigations. Oxford: Blackwell.
Figure 1: Simplified problem space for the set-ordering problem, as described in the text. This diagram does not show states more than once, so not all possible steps from any given problem state are illustrated.
1Since Turing's proof of the universal nature of computation depended on an imaginary device which had infinite storage capacity, it cannot be directly implemented but only simulated.
2Perhaps the most significant variation is the marriage of means-ends analysis to natural selection, which allows a machine to apply a large number of operators to the current state, choose the ones which most reduce the distance to the desired state, and then produce new operators by'breeding'the successful ones (see Holland, 1995; Koza, 1992, 1994). This technique has had an impact in the field of A.I. Its application in cognitive science has so far been limited, but there are signs that this is changing (see Edelman, 1987; Calvin, 1996).
3To appreciate the importance of this change of focus, consider the report in Cytowic (1989, p. 7) that "Norman Geschwind [a reknowned neurologist] related to me that in 1942, at Harvard, professors joked that there were people who thought the brain might be related to behavior, but postulated that it would be hundreds of years before anything came of it and that it was a nonsensical speculation to consider this area."
4In genetic evolution this structure is provided by the fact that small changes in the genome are likely to have small effects on the phenotype. If a space of possibilities is not structured in this way, evolutionary search would be a purely random search. In this case there would be no advantage to the conserving information about past solutions to the problem for which a solution is being evolved, so evolution would never get started.
5A small number of anthropologists and philosophers had begun arguing for the need of taking context into account in understanding human beings decades earlier than cognitive scientists did (see Austin, 1955; Wittgenstein, 1958; Winch, 1958; Garfinkel, 1967; Geertz, 1973).
6Some researchers and educators have erroneously attempted to conclude from the demonstration of these limitations that the topics themselves must necessarily remain difficult and that intuitive understanding of domains such as probability must remain beyond our grasp. It has been shown by Wilensky (1995; 1997) that with the aid of suitable cognitive technologies, these limitations can be circumnavigated and new intuitions developed.
7The term 'intentional' is not used here in its usual sense, but in a technical sense. An intentional state is a state which is directed at some thing, as a desire must be a desire _for_ something, or a belief a belief _about_ something.
8John von Neumann, the brilliant mathematician who contributed so much towards the design of the modern computer, was once given this problem. After thinking for a brief moment, he gave the correct answer. The colleague who had posed the puzzle said "Oh, you saw through it. Most people try to work out a series of decreasing terms and compute the sum." With a puzzled expression in his face, von Neumann is alleged to have replied "But that's just what I did." (Hogan, 1997, p. 52)
E.) Conclusion
Bibliography
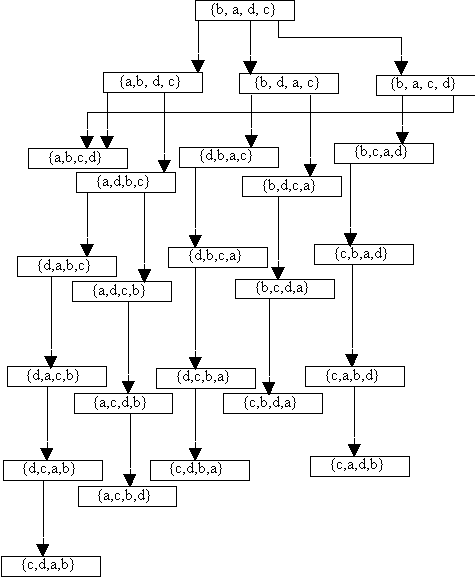
Notes