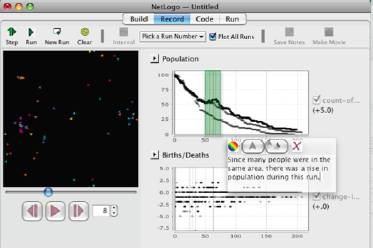
Many of the ideas about rate of change and accumulation that we encounter in science (for example, in population dynamics or the relationship between temperature and pressure in gasses) and in everyday life (for example, climate change or voting trends) reflect complex systems – systems where a single quantitative pattern encapsulates many interacting events and entities. Knowing how students think and learn about change over time in such systems can help educators prepare students as active and informed citizens, provide a new access point to more formal mathematical topics such as calculus and difference/differential equations, and provide a better foundation for students entering the natural and social sciences.

As part of this work, I have developed DeltaTick, a software environment that enables students to construct their own computer simulations from customizable libraries of domain-specific, natural-language building blocks in order to explore how the behaviors and interactions of individuals in a system can generate different mathematical trends. 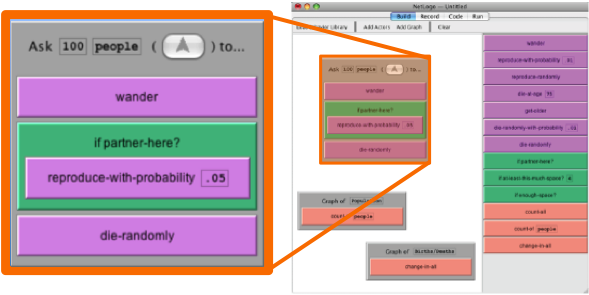My goal is to leverage students’ existing ways of reasoning to democratize access to the ideas of calculus, while also presenting it as a tool for thinking about the patterns that characterize the sciences and everyday life.

I have conducted in-depth interviews and classroom studies using DeltaTick with several high school classes in both high and low performing Chicago Public Schools, and am currently analyzing how students used the software, what they learned, and how to improve its design and accompanying activities moving forward.

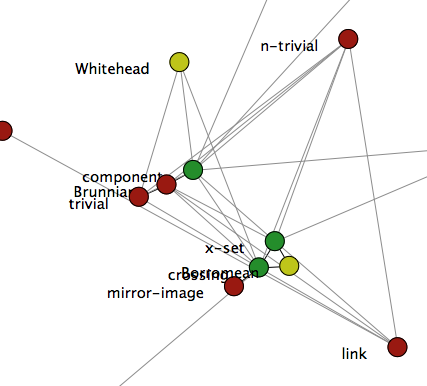
As the world becomes more interconnected, complex systems are becoming increasingly important in science and STEM education. Research shows that learning, too, can be thought of as emerging from the complex interactions between a given learner's existing knowledge, new knowledge and experiences, and artifacts, activities, and other people. To explore these interactions and connections, my work is guided by a theory of learning as the progressive building of a network of resources (including bits of knowledge, representations, tools, and so forth). This perspective leads me to adopt tools from social science such as knowledge analysis, semi-clinical interviews, and interaction analysis along with tools from complexity studies and computer science such as network analysis and computational linguistics to identify the resources that learners use to build an understanding of STEM topics, as well as the processes by which those resources are connected over time.

This approach permeates all of my work, but it is best reflected in my work on expert reasoning, where I identified a number of formal mathematical, informal mathematical, and extra-mathematical resources that experts used to make sense of an unfamiliar mathematical proof. After these resources were identified, I was able to construct temporal network representations of experts' reasoning using the proof. These networks show that different types of knowledge play different structural roles for individual experts. They also show how informal exemplar and everyday concepts play a central role in experts' early sense making, and fade to the periphery as experts build connections to more formal symbolic mathematical knowledge.

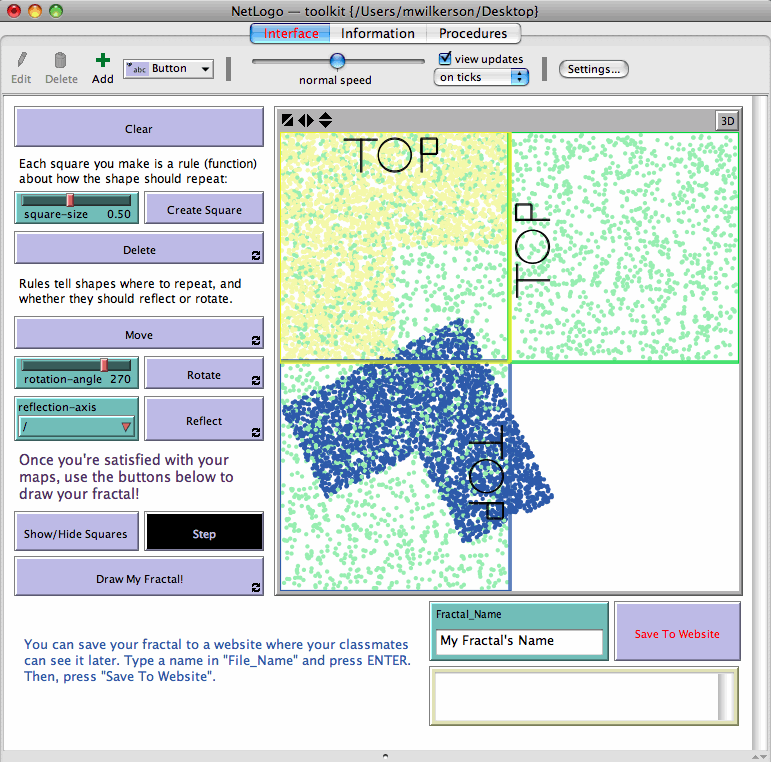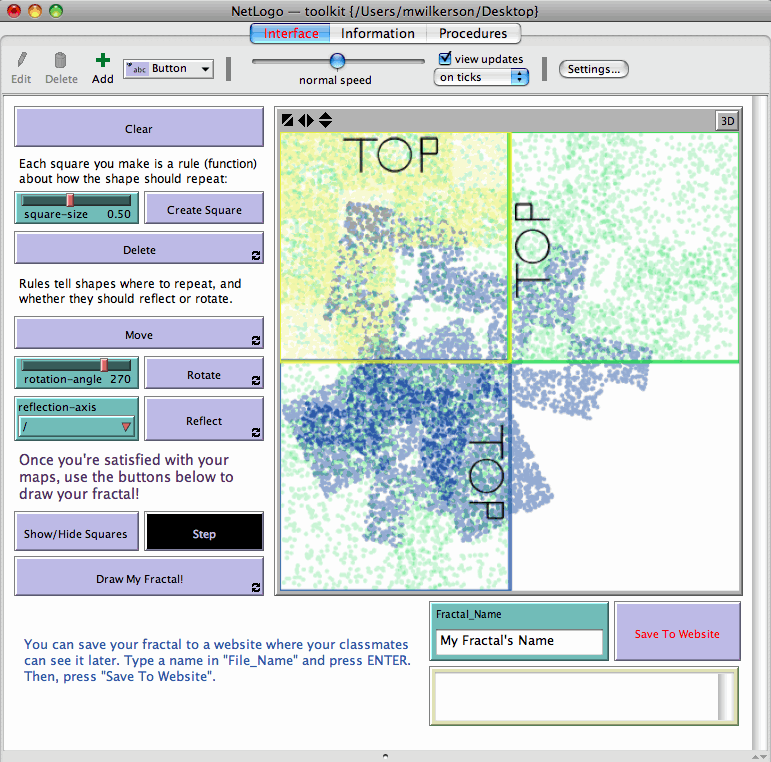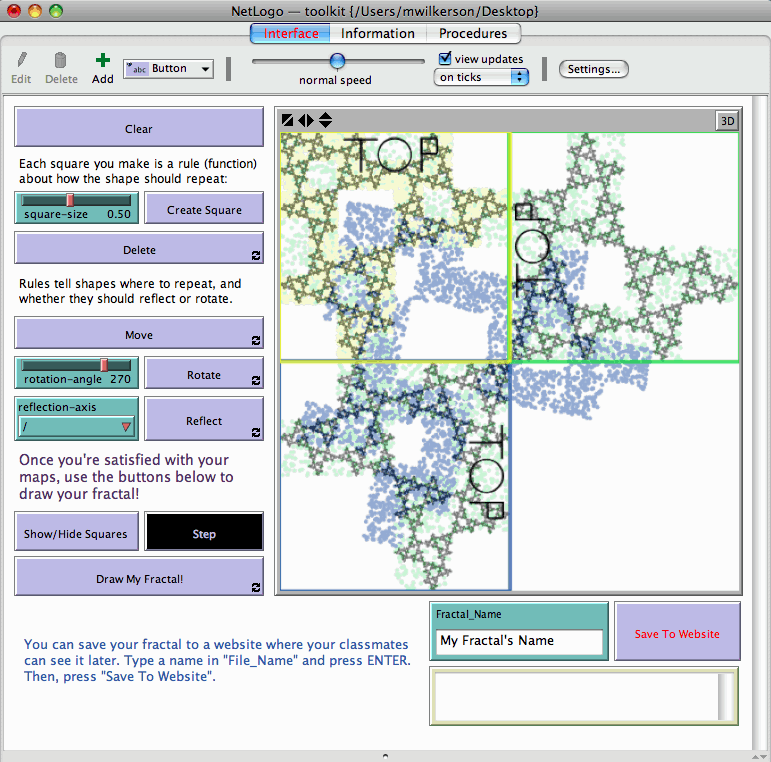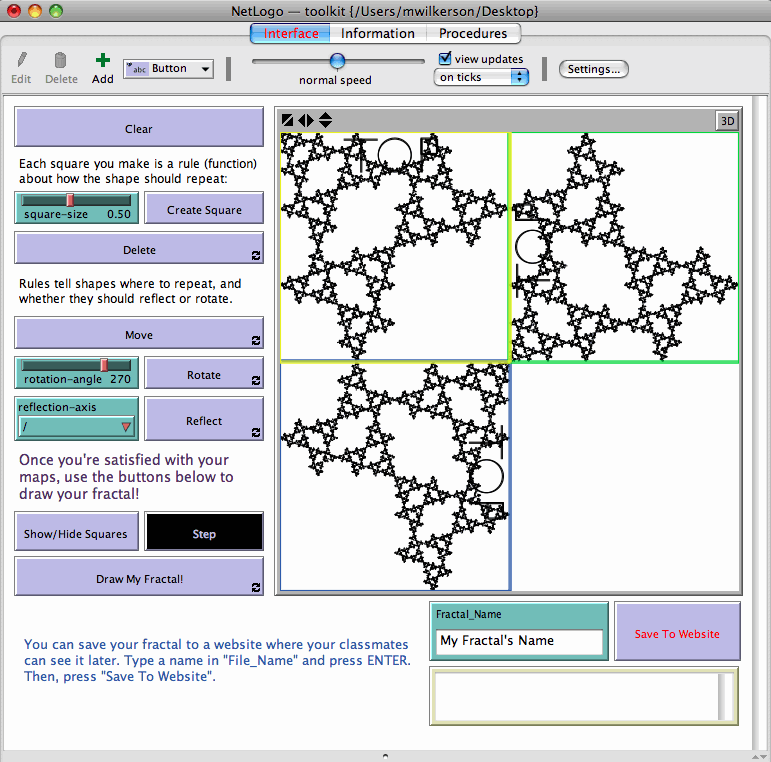
This project emerged from a collaboration with a local K-8 school interested in exploring mathematical connections to nature and art. For this project, I created a tool for students to generate their own fractal structures by “writing” the rules to create those fractals geometrically on a computer screen. The fractals are generated using iterated function systems (IFS), and I was originally (and still am!) interested in how learners might relate their geometric activities on the screen, which define how points in the unit square should map in order to construct the fractal, to set theoretic notions of function. After using this tool in 6th through 8th grade classrooms, however, I noticed another interesting trend - I found that students especially enjoyed sharing and identifying connections, invariances, and themes across the diversity of their peers’ fractals and the rules that generated them.

As a result, I developed the Categorizer, an interactive gallery that allows students to organize their peers’ collection of work under their own thematic schemes. Students can observe the function rules that generated different fractions, create their own categorical schemes for sorting and comparing fractals, and can see an aggregation of their peers' categorization schemes. I have piloted this new addition to the IFS fractal activities, and am excited to investigate the potential that exploring an entire body of student-generated work as an object of analysis and reflection can hold for students’ motivation, analogical reasoning, and learning.

I have had the opportunity to contribute to a number of studies and projects aimed at exploring the potential for agent-based modeling (ABM) to restructure, supplement, and otherwise transform STEM education, broadly conceived. In the MAgICS project, I worked with colleagues to explore the potential for ABM to integrate interdisciplinary and advanced-level topics to introductory computer science, and I have explored the role of visualization and perspective in students' learning from agent-based models in electromagnetism. I have managed the popular NetLogo software's Models Library for several years, personally authored a number of ABMs featured in that Library including 3D GasLab, Flocking Vee Formations, and Surface Walking 2D and 3D, and have contributed as a member of the NetLogo design team.

Before coming to Northwestern, I was an undergrad designer and developer for the Ubiquitous Presenter project, a Tablet PC based classroom lecturing technology developed jointly by the University of California, San Diego and the University of Washington. See more here.

I also did a bit of research as an undergrad in geometric topology, specifically around whether or not Brunnian Links can be made from more than three convex planar curves (spoiler: nope, but I can only show why not for 4 and 5 curves). If that's something that you're into, I'll bring a whiteboard, KnotPlot and some string and we can chat.