ProbLab
A Suite of Models for Experiencing and Relating Micro and Macro Perspectives of Probability
Main Page, Papers & Publications, Models
About ProbLab
ProbLab is a computer-based middle-school curricular unit in probability and statistics designed to enrich student thinking in the domain. The ProbLab unit is part of the Connected Probability project (Wilensky, 1997) and includes a suite of interactive models authored in the NetLogo (Wilensky, 1999) modeling-and-simulation environment and using the HubNet Participatory Simulation technological infrastructure (Wilensky & Stroup, 1999). ProbLab will also soon include related curricular material, such as student worksheets and teacher guides. ProbLab is designed and developed at the Center for Connected Learning and Computer-Based Modeling at Northwestern University and is researched in middle schools in ChicagoLand.
Overview
The field of probability and statistics is challenging for middle school, high school, and even college and graduate-school students. We diagnose students' difficulty as reflecting a disconnect, in prevalent designs, between three constructs that we have come to identify as the interrelated pillars of the domain: theoretical probability, empirical probability, and statistics (see Figure 1, above). Students' disconnected understanding of the domain results both from the designs of prevalent curricula that do not attempt to integrate these pillars and from the consequential absence of visual metaphors to support students' construction of the domain as a set of coherent and integrated connections.
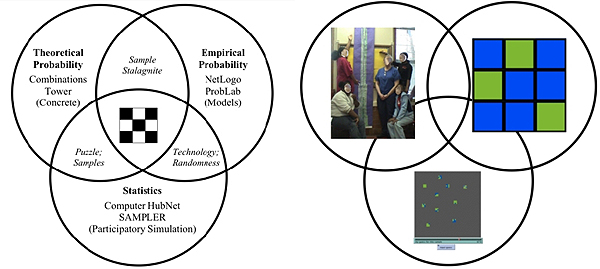
ProbLab's design rationale and interactive materials are constituted on the domain triad. The above diagram is more than a blueprint for designing classroom tools and activities for this specific domain. The structure of the diagram reflects our view of learning in general as the process of student construction of connections between existing understandings that are evoked through participaing in classroom activities around the design tools. Each understanding is a necessary fragment for the new domain, yet these understandings need to be woven together in and through using the new domain tools. That is, we see each pillar as a node in a semiotic web -- each construct is meaningful only in light of its implicit relations within this structure. So it is not too effective to have students learn each of the pillars in isolation -- students may learn rote solution procedures, but these procedures may not be grounded in their experience. Students build meaning for each construct through negotiating back and forth along the domain dialectics that are designed into classroom tools and activities. We call these domain dialectics the learning axes of the domain (Abrahamson & Wilensky, 2004). The learning axes are spaces of potential learning that extend between the pillars, such as between theoretical probability and empirical probability -- students learn by dwelling in the tensions created by these axes -- tensions that are enhanced through experiments, problems, and riddles. For each of these designated axes we have created bridging tools (Abrahamson, 2004), such as 9-Block Stalagmite, a NetLogo model that helps students bridge between theoretical and empirical probability. These bridging tools are "ambiguous." They are designed to evoke in students intuitions for each of the two nodes of the learning axis -- the tools afford schemes related to both nodes. Thus, students ground in the bridging tools the necessary complementary perspectives for constructing meaning for the domain. That is, by alternating between interpretations of these objects, students have opportunities to reconcile the inherent tensions of the learning axis, and this reconciliation fosters connected knowledge of the domain.

Students explore connections between the domain pillars by constructing and experimenting with domain bridging tools, such as the 9-block. The 9-block is a 3-by-3 array of squares, each of which is either green or blue (see Figure 1, above, in the center of the 'Design Rationale' triad and in Figure 1 and Figure 2 in the various classroom tools). The 9-block is what we call the math-thematical object of the ProbLab unit (the pivotal and multi-faceted bridging tool of the design). A 9-block is at once one of all 512 permutations in its combinatorial sample space (theoretical probability), a randomly generated compound event of 9 independent blue/green events (empirical probability), and a sample out of a population of squares (statistics).
Research Sites and Collaborations
ProbLab is researched in middle schools in ChicagoLand. This research is partly funded by the The National Science Foundation. In Chicago Public Schools, we have been collaborating with Stone Scholastic Academy. In District 65, we have been collaborating with Nichols Middle School. ProbLab is also being used by independent educators, whose insights and feedback are highly beneficial to our ongoing design process.
Acknowledgements
We gratefully acknowledge the support of the National Science Foundation.